Навигация
Развитие алгебры до Ф. Виета
116991
знак
7
таблиц
2
изображения
2.1 Развитие алгебры до Ф. Виета.
2.1.1 Алгебра греков.
Считается, что эллины заимствовали первые сведения по геометрии у египтян, по алгебре - у вавилонян.
В древнейших египетских источниках папирусе Райнда и Московском папирусе - находим задачи на «аха» (термин «аха» означает «куча», «груда»). Имеется в виду некоторое количество, неизвестная величина, подлежащая определению) соответствующие современным линейным уравнениям, а также квадратным вида ах2 = b. В вавилонских клинописных текстах имеется большое число задач, решаемых с помощью уравнений и систем первой и второй степеней, которые записаны без символов, но в специфической терминологии. В этих текстах решаются задачи, приводящие к трехчленным квадратным уравнениям вида ах2 - bх = с или х2 - рх = q. В задачах на «аха» можно обнаружить зачатки алгебры как науки о решении уравнений.
Но если вавилоняне за два тысячелетия до нашей эры умели числовым путем решать задачи, связанные с уравнениями первой и второй степеней, то развитие алгебры в трудах Евклида (365 - ок. 300 гг. до н. э.), Архимеда (287-212 гг. до н. э.) и Аполлония (ок. 260-170 гг. до н. э.) носило совершенно иной характер: греки оперировали отрезками, площадями, объемами, а не числами. Их алгебра строилась на основе геометрии и выросла из проблем геометрии. В XIX в. совокупность приемов древних получила название геометрической алгебры.
В качестве примера геометрической алгебры греков рассмотрим решение уравнения х2 + ax = b2.
Античные математики решали эту задачу построением и строили искомый отрезок так, как показано на рисунке.
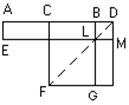
На заданном отрезке АВ (равном a) строили прямоугольник AM со сторонами (а + х) и x, равновеликий данному квадрату (b2), таким образом, чтобы избыточная над прямоугольником AL (равная ах) площадь ВМ была квадратом, по площади равным х2. Сторона этого квадрата и давала искомую величину х. Такое построение называли гиперболическим приложением площади.
Далее, полагая задачу решенной, делили АВ пополам точкой С, на отрезке LM строили прямоугольник MG, равный прямоугольнику ЕС. Тогда прямоугольник AM будет разностью квадратов DF и LF. Эта разность и квадрат LF известны, поэтому по теореме Пифагора можно получить квадрат DF. После этого находили величину DC (равную ½a + x) и DB (равную х).
Геометрическое построение в точности соответствует преобразованию, с помощью которого в современных обозначениях решается уравнение указанного типа:
b2 = ax + х2 = 
– 
Конечно же, при таких построениях отыскивались только положительные корни уравнений: отрицательные числа появились в математике значительно позже.
С помощью геометрии древним удавалось также доказывать многие алгебраические тождества. Но каковы эти доказательства! Они безупречны в отношении логики и слишком громоздки. Вот как формулирует Евклид теорему, выражающую тождество (а + b)2 = a2 + 2аb + b2. Если отрезок (ab) разделен в точке (g) на два отрезка, то квадрат, построенный на (ab), равен двум квадратам на отрезках (ag, gb) вместе с удвоенным прямоугольником на (ag, gb).
Естественно, связывая число с геометрическим образом (линией, поверхностью, телом), древние оперировали только однородными величинами; так, равенство было возможно для величин одинакового измерения.
Такое построение математики позволило античным ученым достигнуть существенных результатов в обосновании теорем и правил алгебры, но в дальнейшем оно стало сковывать развитие науки.
Приведенные примеры могут создать ощущение, что математика древних греков примитивна. Но это не так: созданная ими математика по своему идейному содержанию глубока и питала идеями и методами математику вплоть до XVII в. - века научной революции; многие идеи древних получили дальнейшее развитие в новой математике, созданной усилиями выдающихся умов XVI—XVII вв.
Накопленные в странах Древнего Востока знания состояли из набора разрозненных математических фактов, рецептур для решения некоторых конкретных задач и не могли обладать достаточной строгостью и достоверностью. Создание основ математики в том виде, к которому мы привыкли при изучении этой науки в школе, выпало на долю греков и относится к VI—V вв. до н. э. С этого времени начала развиваться дедуктивная математика, построенная на строгих логических доказательствах.
2.1.2 Алгебра Диофанта.
Новый подъем античной математики относится к III в. н. э., он связан с творчеством великого математика Диофанта. Диофант возродил и развил числовую алгебру вавилонян, освободив ее от геометрических построений, которыми пользовались греки.
У Диофанта впервые появляется буквенная символика. Он ввел обозначения: неизвестной z, квадрата d
), куба c, четвертой dd (квадратоквадрат), пятой dc (квадратокуб) и шестой степеней ее, а также первых шести отрицательных степеней, т. е. рассматривал, величины, записываемые нами в виде x6, x5, x4, x3, x2, x, x-1, x-2, x-3, x-4, x-5, x-6. Диофант применял знак равенства (символ i) и знак 
для обозначения вычитания.
Диофант сформулировал правила алгебраических опeраций со степенями неизвестной, соответствующие нашим умножению и делению степеней с натуральными показателями (для m + n 
6), и правила знаков при умножении. Это дало возможность компактно записывать многочлены, производить умножение их, оперировать с уравнениями. Он указал также правила переноса отрицательных членов уравнения в другую часть его с обратными заиками, взаимного уничтожения одинаковых членов в обеих частях уравнения.
«Арифметика» посвящена проблеме решения неопределенных уравнений. И хотя Диофант считает число собранием (а это означает, что рассматриваются только натуральные числа), при решении неопределенных уравнений он не ограничивается натуральными числами, а отыскивает и положительные рациональные решения.
Неопределенными уравнениями до Диофанта занимались математики школы Пифагора в связи с пифагоровой теоремой. Они искали тройки целых положительных чисел, удовлетворяющих уравнению x2 + y2 = z2.
Диофант поставил задачу установить разрешимость (в рациональных числах) и в случае разрешимости найти рациональные решения уравнения F (х, у) = 0, где левая часть – многочлен с целыми или рациональными коэффициентами. Он исследовал неопределенные уравнения второй, третьей и четвертой степеней и системы неопределенных уравнений.
Во второй книге «Арифметики» он так исследует, например, уравнение второго порядка F (х, у) = 0.
Это уравнение задает коническое сечение. Всякому рациональному решению уравнения соответствует точка кривой с рациональными координатами. Пусть a, b – такие координаты, т. е. F (a, b) = 0.
Диофант делает подстановку у = b + k (х – а), или y = b + kt, х = а + t.
Тогда F (а + t, b + kt) = F (a, b) + tA (а, b) + ktB (а, b) + t2C (a, b, k) = 0.
Но F (a, b) = 0, поэтому t = –
.
Это означает, что каждому рациональному значению параметра k соответствует рациональное же значение t, а значит, рациональная точка кривой. Очевиден геометрический смысл решения: через рациональную точку кривой (a, b) проводится прямая y – b =k (x – a) и находятся вторая точка ее пересечения с кривой.
Методы Диофанта впоследствии применяли и развивали арабские ученые, Виет (1540—1603), Ферма, Эйлер (1707—1783), Якоби (1804—1851), Пуанкаре (1854—1912).
Оценивая творчество Диофанта, Цейтен отмечает существенную деталь: «Наконец, мы желаем здесь вкратце указать на важную роль, сыгранную впоследствии сочинениями Диофанта. Благодаря тому, что определенные уравнения первой и второй степени были облечены у него в численную оболочку они оказались гораздо более доступными для людей, не посвященных еще в культуру греческой математики; более доступными, чем те абстрактные геометрические формы, которые принимают у Евклида уравнения второй степени и которые мы встречаем в сохранившихся до нас трудах других геометров для выражения уравнений первых двух степеней. Поэтому Диофант и явился главным посредником в процессе усвоения греческой алгебры арабами, благодаря которым, в свою очередь она проникла в Европу в эпоху возрождения наук».
Похожие работы
... neat as ninepence - чистенький, аккуратный; с иголочки; a twice-told tale - старая история, что-либо часто повторяемое и потому хорошо известное. 2. Значения числовых компонентов в английских фразеологических единицах Имена числительные, являясь абстрактным показателем количества однородных предметов, обозначением их счета, замкнуты в своеобразную категорию количественных слов, которые лишены ...
... схемы; 9) способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики, как геометрия, Сторонники шестого подхода считают, что математическое мышление является мышлением теоретическим и имеет такую же последовательность становления от эмпирического к аналитическому, к планирующему, рефлексирующему (Р. Атаханов, В.В. Давыдов, Ле Тхи Кхань Кхо, ...
... с активными познавательными обследовательскими действиями, со способностью к замещению предметов посредством условных знаков, символов».(7,с.126) 3. Моделирование в развитии математических представлений дошкольников Поиск эффективных средств познавательного развития детей, выявление условий становления познавательной деятельности в дошкольном детстве является темой научных работ многих ...
... заданное его качество, определение оптимальных (с точки зрения принятого критерия) норм дежурного обслуживания, надобность в котором возникает непланомерно, нерегулярно. С использованием метода математического моделирования можно определить, например, оптимальное количество автоматически действующих машин, которое может обслуживаться одним рабочим или бригадой рабочих и т.п. Типичным примером ...
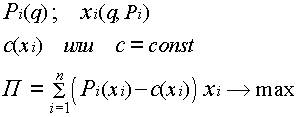
0 комментариев