Навигация
4.1 Алгебра высказываний.
Эта тема важна для школьной математики. Не овладев ее основными действиями, нельзя понять последующие темы, как, не овладев таблицами сложения и умножения, нельзя научиться арифметике и тем более алгебре.
Исходные объекты алгебры высказываний – это простые высказывания. Их будем обозначать строчными латинскими буквами a, b, c, …, x, y, z. Предполагается, что всякое простое высказывание обладает одним и только одним из двух свойств: либо оно истинно, либо ложно.
Будем пользоваться почти повсеместно принятой терминологией: свойства истинности (и) и ложности (л) мы будем называть значениями истинности высказываний. При такой терминологии значение истинности сложного высказывания есть функция от значений истинности простых высказываний; такая функция называется логической связкой.
4.1.1 Определения основных логических связок
а) Отрицание (знак ù ). Если а – высказывание, то ùа (читается: «не а») также высказывание; оно истинно или ложно в зависимости от того, ложно или истинно высказывание а.
Таким образом, операция отрицания описывается следующей таблицей:
| a | ùa |
| и | л |
| л | и |
Мы видим, что операция ù в теории высказываний вполне соответствует понятию отрицания в обыденном смысле слова. Если, например, а – высказывание «Число три делит число шесть», то отрицанием ùа этого высказывания будет «Число три не делит число шесть». Высказывание а при этом истинно, высказывание ùа, – ложно.
Если же в качестве высказывания а взять какое-нибудь ложное высказывание, например «Число три делит число пять», то его отрицание ùа будет высказывание «Число три не делит число пять» - истинное высказывание.
б) Конъюнкция. В качестве знака для конъюнкции мы будем употреблять знак Ù (можно также &).
Если а и b - высказывания, то а Ù b (читается: «а и b») – новое высказывание; оно истинно тогда и только тогда, когда а истинно и b истинно.
В отличие от операции отрицания, зависящей от одного элементарного высказывания, конъюнкция, как и все последующие приводимые нами связки, зависит от двух элементарных высказываний, поэтому они называются двуместными связками, отрицание же - связка одноместная.
Для задания двуместных связок удобно записывать матрицы истинности в виде таблиц с двумя входами: строки соответствуют значениям истинности одного элементарного высказывания, столбцы – значениям другого элементарного высказывания, а в клетке пересечения столбца и строки помещается значение истинности соответствующего сложного высказывания.
Значение истинности сложного высказывания а Ù b задается матрицей
| b a | и | л |
| и | и | л |
| л | л | л |
Как видно, определение операции конъюнкции вполне соответствует обыденному значению союза «и»:
в) Дизъюнкция. В качестве знака для дизъюнкции мы будем употреблять знак Ú.
Если а и b – высказывания, то а Ú b (читается: «а или b») – новое высказывание, оно ложное, если а и b ложны; во всех остальных случаях а Ú b истинно.
Таким образом, матрица истинности для операции дизъюнкции выглядит так:
| b a | и | л |
| и | и | и |
| л | и | л |
Операция дизъюнкции довольно хорошо соответствует обыденному значению союза «или».
Примеры.
«Три делит пять или три больше шести» ложно;
«Три делит шесть или три больше шести» истинно;
«Три делит шесть или три меньше шести» истинно.
г) Импликация. В качестве знака для импликации будем употреблять знак Þ.
Если а и b – два высказывания, то а Þ b (читается: «а имплицирует b») – новое высказывание; оно всегда истинно, кроме того случая, когда а истинно, а b ложно.
Матрица истинности операции импликации следующая:
| b a | и | л |
| и | и | л |
| л | и | и |
В импликации а Þ b первый член а называется антецедентом, второй b – консеквентом.
Операция Þ описывает в некоторой мере то, что в обыденной речи выражается словами «Если а, то b», «Из а следует b», «а – достаточное условие для b», но на этой аналогии не следует слишком настаивать. Действительно, учитывая определение импликации, данное выше, и интерпретируя выражение а Þ b как «если а, то b», мы получаем: «Если дважды два – четыре, то трижды три – девять» – истинное высказывание; «Если дважды два – пять, то трижды три – восемь» – истинное высказывание и только высказывание типа «Если дважды два – четыре, то трижды три – восемь» ложно.
По определению импликации сложное высказывание а Þ всегда истинно, если консеквент истинный или если антецедент ложный, что в очень малой мере отражает обыденное значение выражения «Если а, то b» или «Из а следует b». Ни в какой мере не следует рассматривать высказывание импликации как означающее, что антецедент является причиной, а консеквент — следствием в том смысле, как это понижается в естественных науках.
Несколько позже мы убедимся, что операция импликации достаточно точно выражает понятие логического следования в той форме, как оно употребляется в математике.
д) Эквиваленция. Для этой операции мы будем употреблять знак Û. Операция эквиваленции определяется так: если а и b – два высказывания, то а Û b (читается: «а эквивалентно b»; Û соответствует словесному выражению «...тогда и только тогда, когда...») – новое высказывание, которое истинно, если либо оба высказывания истинны, либо оба – ложны.
Из этого определения связки Û следует, что ее матрица истинности выглядит так:
| b a | и | л |
| и | и | л |
| л | л | и |
Введенными пятью связками (ù, Ù, Ú, Þ, Û) мы ограничимся.
С помощью уже введенных связок мы можем строить сложные высказывания, зависящие не только от двух, но и от любого числа элементарных высказываний.
Отметим в этой связи, что так называемое нестрогое неравенство а £ b (читается: a меньше или равно b») представляет собой дизъюнкцию (а < b) Ú (a = b); оно истинно, если истинно по меньшей мере одно из входящих в него простых высказываний. Хорошими примерами сложных высказываний, встречающихся в школьной практике, являются так называемые двойные неравенства. Так, формула а < b < с означает (а < b) Ù (b < с), а, например, а < b £ c означает сложное высказывание (а < b) Ù ((b < c) Ú (b = c)).
Построение сложных высказываний делается аналогично тому, как в элементарной алгебре с помощью операций сложения, вычитания, умножения и деления строятся сколь угодно сложные рациональные выражения. А именно, предположим, что мы уже построили два каких-нибудь сложных высказывания, которые мы ради удобства сокращенно обозначим большими латинскими буквами А и В (при этом мы условимся, что элементарные высказывания следует рассматривать как частный случай сложных). Тогда новые высказывания можно получить, соединив А и В одним из знаков Ù, Ú, Þ, Û или же построив высказывание ùА и заключив результат в скобки. Сложными высказываниями будут, например, высказывания следующего вида:
((а Þ b) Ù (с Ú а)); ((а Þ b) Û (с Þ ùа)).
При этом предполагается, что встречающиеся здесь буквы являются сокращенными обозначениями каких-либо высказываний.
Таким образом, в принципе зная эти высказывания, можно было бы построить русские фразы, выражающие эти сложные высказывания. Только словесное описание сложных высказываний быстро становится малообозримым, и именно введение целесообразной символики позволяет проводить более глубокое и точное исследование логических связей между различными высказываниями.
Располагая значением истинности простых высказываний, легко подсчитать на основании определения связок значение истинности сложного высказывания. Пусть, например, дано сложное высказывание
((bÚ с) Û (b Ù a))
и пусть входящие в него элементарные высказывания имеют следующие значения истинности: а = л, b = и, с = и. Тогда b Ú с = и, b Ù a = л, так что (( bÚ с) Û (b Ù а)), т. е. рассматриваемое высказывание ложно.
Похожие работы
... neat as ninepence - чистенький, аккуратный; с иголочки; a twice-told tale - старая история, что-либо часто повторяемое и потому хорошо известное. 2. Значения числовых компонентов в английских фразеологических единицах Имена числительные, являясь абстрактным показателем количества однородных предметов, обозначением их счета, замкнуты в своеобразную категорию количественных слов, которые лишены ...
... схемы; 9) способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики, как геометрия, Сторонники шестого подхода считают, что математическое мышление является мышлением теоретическим и имеет такую же последовательность становления от эмпирического к аналитическому, к планирующему, рефлексирующему (Р. Атаханов, В.В. Давыдов, Ле Тхи Кхань Кхо, ...
... с активными познавательными обследовательскими действиями, со способностью к замещению предметов посредством условных знаков, символов».(7,с.126) 3. Моделирование в развитии математических представлений дошкольников Поиск эффективных средств познавательного развития детей, выявление условий становления познавательной деятельности в дошкольном детстве является темой научных работ многих ...
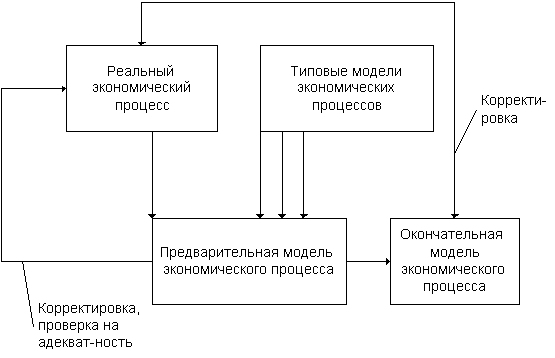
... заданное его качество, определение оптимальных (с точки зрения принятого критерия) норм дежурного обслуживания, надобность в котором возникает непланомерно, нерегулярно. С использованием метода математического моделирования можно определить, например, оптимальное количество автоматически действующих машин, которое может обслуживаться одним рабочим или бригадой рабочих и т.п. Типичным примером ...
0 комментариев