Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов нечетной степени

6. Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов нечетной степени

Рассмотрим решение неравенств, содержащих переменную под знаком двух радикалов нечетной степени. Решение проводится также путем последовательного возведения обеих частей неравенства в соответствующую степень и преобразования его в неравенство, не содержащее радикалов. При возведении неравенства в нечетную степень эквивалентность не нарушается. Имеют место следующие эквивалентные преобразования:

Пример 1. Решить неравенство

Решение. Возводим обе части неравенства в куб:

Ответ: .

Рассмотрим отдельно решение неравенств вида:

После возведения его в куб получим неравенство

.

Многократное возведение в куб неравенства в общем случае не приводит к освобождению от радикалов. Для решения таких неравенств целесообразно использовать метод интервалов. Суть его заключается в следующем.

Пусть требуется решить неравенство вида:

(1)

или

(2)

Сначала установим, при каких значениях переменной левая часть неравенства равна правой его части, то есть решим иррациональное уравнение, которое назовем соответствующим

(3)

Далее находим область определения данного неравенства (она совпадает с областью определения соответствующего уравнения). Затем наносим корни уравнения (3) на числовую ось, на которой отмечаем также область определения неравенства. Пусть, например, область определения неравенства (1) или (2) состоит из двух числовых промежутков и , , , , - корни уравнения (3).

Корни уравнения (3) разбивают область определения неравенства на промежутки знакопостоянства. Функция меняет знак при переходе через корень нечетной кратности, а в промежутках между корнями знак функции постоянный. В рассматриваемом на рисунке примере такими числовыми промежутками будут промежутки , , , , .

Далее определяем в каждом из отмеченных числовых промежутков знак функции . Для определения знака функции достаточно взять любое число из соответствующего промежутка. подставить в функцию вместо переменной и установить знак полученного числового выражения. Те числовые промежутки, в которых функция положительная, будут решением неравенства (1), ибо любое значение переменной, взятое из этих числовых промежутков, обращает его в истинное числовое неравенство. Остальные числовые промежутки образуют множество решений неравенства (2).

Пример 2. Решить неравенство

Решение. Сначала находим решение соответствующего уравнения

возведем уравнение в куб:

Так как по условию выражение должно равняться , то, сделав соответствующую замену, получим:

Возведем уравнение в куб и найдем искомые значения переменной: и .

Проверка 1.

- ложно, корень - посторонний.

Проверка 2.

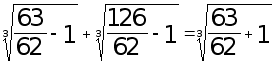
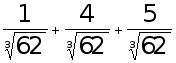- истинно, - корень уравнения.

Областью определения неравенства является множество действительных чисел. Корень соответствующего уравнения разбивает числовую ось на два числовых промежутка:

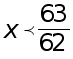и .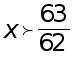

Взяв любое число (например, ) из первого промежутка и подставив в неравенство, получим . Значит, числовой промежуток не входит в решение неравенства. Значение , взятое из числового промежутка 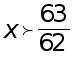, обращает данное неравенство в истинное числовое неравенство . Значит, числовой промежуток 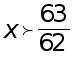является решением неравенства.

Ответ: .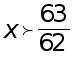

Пример 3. Решить неравенство

Решение. Решим соответствующее уравнение

после возведения в куб обеих частей уравнения получим

сделаем подстановку получим уравнение

и

Отмечаем корни на числовой оси

Областью определения неравенства являются все действительные числа, поэтому рассматриваем три числовых промежутка: , , . Пусть , тогда - ложное числовое неравенство. Значит числовой промежуток не входит в решение. Пусть , тогда - истинное числовое неравенство и числовой промежуток входит в решение. Аналогично, числовой промежуток тоже входит в решение.

Ответ: , .

Пример 4. Решить неравенство

Решение. Возведем в куб части неравенства:

откуда

ОДЗ неравенства или .

При значения всегда, а . Значит последнее неравенство истинно при .

Ответ: .

Пример 5. Решить неравенство

Решение. Возведем обе части неравенства в куб, предварительно перенеся в правую часть:

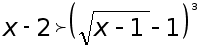
Последнее неравенство эквивалентно системе неравенств

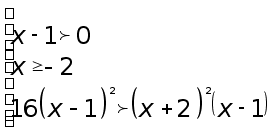
или

Решением последней системы является .

Ответ: .

Похожие работы

Психолого-педагогическое обоснование внеклассной работы по математике

Скачать

113174

0

0

... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...

Специальная педагогика

Скачать

899509

4

0

... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...

Исторические экскурсы в курсе алгебры 7 класса как средство развития познавательного интереса

Скачать

70672

3

3

... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...

Подготовка к Единому государственному экзамену по математике через элективные курсы

Скачать

45824

3

0

... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...