Навигация
Некоторые замечательные кривые
Министерство образования и науки РФ
Череповецкий государственный университет
Институт информационных технологий
Кафедра прикладной математики
Дисциплина: Геометрия и алгебра
Курсовая работа
на тему «Некоторые замечательные кривые»
г. Череповец
2010-2011 уч.г.
Содержание
Введение
1. Строфоида
1.1 Определение
1.2 Исторические сведения
1.3 Стереометрическое образование
1.4 Особенности формы
1.5 Задача
2. Циссоида Диокла
2.1 Определение и построение
2.2 Исторические сведения
2.3 Площадь S полосы
2.4 Объем V тела вращения
2.5 Задача
3. Декартов лист
3.1 Исторические сведения
3.2 Построение
3.3 Особенности формы
3.4 Задача
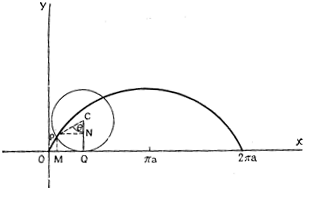
4. Улитка Паскаля
4.1 Определение и построение
4.2 Исторические сведения
4.3 Особенности формы
4.4 Свойства нормали
4.5 Построение касательной
4.5 Задача
5. Лемниската Бернулли
5.1 Определение
5.2 Исторические сведения
5.3 Построение
5.4 Особенности формы
5.5 Свойства нормали
5.6 Построение касательной
5.7 Задача
Заключение
Используемая литература
Введение
В данной работе мы рассмотрим некоторые замечательные кривые и их особенности.
В параграфе 1 будет рассмотрена строфоида, особенности её формы, стереометрическое образование и исторические сведения.
Во 2-м параграфе мы изучим циссоиду Диокла и некоторые формулы, связанные с ней.
В параграфе 3 узнаем метод построения, особенности формы и исторические сведения о кривой, называемой «Декартов лист».
В 4-м параграфе рассмотрим улитку Паскаля. Её определение, построение, особенности формы, свойства нормали и построение касательной. плоский кривой лемниската бернули строфоида
В параграфе 5 будет изучена лемниската Бернулли: определение, построение, исторические сведения, особенности формы, свойства нормали и построение касательной.
А также при помощи задач узнаем формулы кривых в прямоугольной декартовой и полярной системах координат.
1. Строфоида
1.1 Определение.
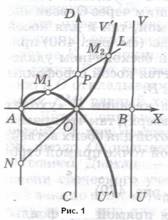
Прямая строфоида, или просто строфоида, определяется так: берём взаимно-перпендикулярные прямые AB, CD (рис.1) и на одной из них точку A; через неё проводим произвольую прямую AL, пересекающую CD в точке P. На AL откладываем отрезки PM1,, PM2 равные PO (O – точка пересечения AB и CD). Строфоида (прямая) есть геометрическое место точек M1,M2.
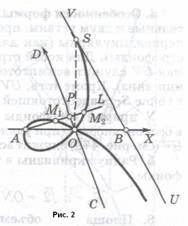
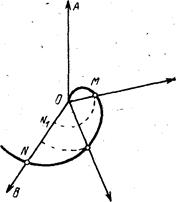
Косая строфоида (рис.2) строится аналогично с той разницей, что AB и CD пересекаются косоугольно.
1.2 История вопроса
Строфоида была рассмотрена (вероятно, впервые) Ж. Робервалем в 1645 г. под именем птероиды. Нынешнее название введено Миди в 1849 г.
1.3 Стереометрическое образование
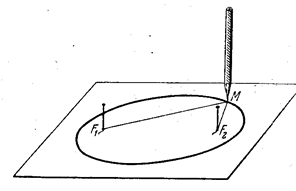
Представим себе цилиндрическую поверхность с осью CD (см. рис.1) и радиусом AO. Через точку A проведем перпендикулярную плоскости чертежа произвольную плоскость K (прямая AL – след этой плоскости). В сечении получим эллипс; его фокусы M1, M2 описывают прямую строфоиду.
Косая строфоида строится аналогично с той лишь разницей, что цилиндрическая поверхность заменяется конической: ось конуса (OS на рис.2) проходит через O перпендикулярно AB; прямая UV, проходящая через B параллельно CD, – одна из образующих. Точки M1, M2 – фокусы соответствующего конического сечения; косая строфоида расположена на обеих полостях конической поверхности и проходит через вершину S последней.
1.4 Особенности формы
Точка O – узловая; касательные к ветвям, проходящим через O, взаимно перпендикулярны (как для прямой, так и для косой строфоиды). Для косой строфоиды (рис.2) прямая UV служит асимптотой (при бесконечном удалении вниз). Кроме того, UV касается косой строфоиды в точке S, равноотстоящей от A и B.
У прямой строфоиды точка касания S «уходит в бесконечность» (при удалении вверх), так что прямая UV (см. рис.1) служит асимптотой для обеих ветвей.
1.5 Задача
Написать уравнение строфоиды в прямоугольной декартовой системе координат, осями которой являются прямые AB и CD, а направление оси OX определяется направлением оси строфоиды.
Решение:
Пусть O – начало координат; ось OX направлена по лучу OB; AO=a, ![]() AOD=α; когда строфоида – косая, система координат – косоугольная, ось OY направлена по лучу OD:
AOD=α; когда строфоида – косая, система координат – косоугольная, ось OY направлена по лучу OD:
![]() (1)
(1)
Для прямой строфоиды уравнение (1) приводится к виду
![]() .
.
Похожие работы
... этим лучом и касательной к спирали, проведенной в точке пересечения (Рис. 13). Теорема Паскаля Б. Паскалю (1623—1662) не было еще и 17 лет, когда он открыл замечательное общее свойство конических сечений. Об его открытии математикам поведала афиша, отпечатанная в количестве 50 экземпляров; только два из них дошли до нашего времени. Несколько таких афиш были расклеены на стенах домов и церквей ...
... , повысить интерес к учению; 3) углубить знания, полученные на уроках математики. Ход занятия I. Организационный момент II. Основная часть 1) Лекция об истории изучения плоских кривых [см. гл. I § 1] 2) Задание Ребята, разгадаем с вами кроссворд: ПАСКАЛЬ ПАПИРУС АПОЛЛОНИЙ РОБЕРВАЛЬ АРХИМЕД ГЕОМЕТРИЯ По горизонтали 1. Учёный, считавший, что дуга спирали ...
... различных видах деятельности; • развитии пространственного воображения и пространственных представлений, образного, пространственного, логического, абстрактного мышления школьников; • формировании умений применять геометро-графические знания и умения для решения различных прикладных задач; • ознакомлении с содержанием и последовательностью этапов проектной деятельности в области технического и ...
... , поскольку точки М и М’ входят в формулу равноправно, а для центра инверсии и бесконечно удаленной области все очевидно. 1.3. Формула инверсии в комплексно сопряженных координатах. Найдем формулу обобщенной инверсии при задании точек комплексными числами. Пусть точкам S, M и М’ соответствуют комплексные числа s, z и z’. По формуле скалярного произведения векторов . Коллинеарность точек S, M и ...



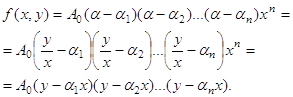







0 комментариев