Навигация
3. Формула парабол (Сімпсона).
Метод Сімпсона найпоширеніший і простіше застосовний для програмування. Його суть полягає в наближенні підінтегральної функції відрізками парабол.
Отже, розглянемо спочатку інтеграл 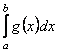 , де
, де ![]() – парабола;
– парабола; ![]() ,
,![]() ,
,![]() – деякі параметри (або числа).
– деякі параметри (або числа).
Тоді


Нехай тепер маємо інтеграл 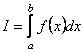 , де
, де ![]() - неперервна на інтервалі
- неперервна на інтервалі![]() функція. Якщо інтервал розбити на п рівних частинок
функція. Якщо інтервал розбити на п рівних частинок ![]() , i=0,1,…n-1,, то заданий інтеграл І можна записати так:
, i=0,1,…n-1,, то заданий інтеграл І можна записати так:
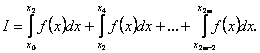
Якщо на кожному з інтегралів для проміжків ![]() функцію
функцію ![]() замінимо параболами
замінимо параболами ![]() , що проходять через точки
, що проходять через точки ![]() ,то одержимо
,то одержимо
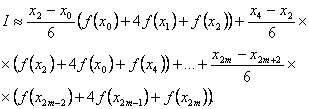
Через те, що, формула матиме вигляд:
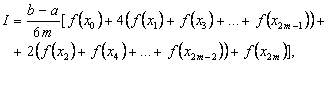 або
або

![]() (4)
(4)
Формула (4) називається формулою парабол або Сімпсона. Доведено, що похибка обчислень ![]() за формулою Сімпсона є такою:
за формулою Сімпсона є такою:
![]() (5)
(5)
Проте, цією оцінкою похибки можна користуватись, якщо ![]() є хоча б чотири рази диференційовною. Але, якщо
є хоча б чотири рази диференційовною. Але, якщо ![]() навіть чотири рази диференційовна, то часто оцінка четвертої похідної
навіть чотири рази диференційовна, то часто оцінка четвертої похідної ![]() може виявитись досить складною. Тому на практиці переважно користуються таким методом: обчислюють інтеграл, розділяючи інтервал, заданий границями інтегрування, один раз на n рівних частин, а другий раз на т частин. Якщо одержані двоє значень інтеграла мало відрізняються, то результат можна вважати прийнятним. Порівнюючи їх можна оцінити і точність обчислень.
може виявитись досить складною. Тому на практиці переважно користуються таким методом: обчислюють інтеграл, розділяючи інтервал, заданий границями інтегрування, один раз на n рівних частин, а другий раз на т частин. Якщо одержані двоє значень інтеграла мало відрізняються, то результат можна вважати прийнятним. Порівнюючи їх можна оцінити і точність обчислень.
Приклад. Обчислити з точністю до 0,001 інтеграл
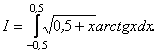
Р о з в ’ я з у в а н н я. За формулою (4) маємо:
при при
|
|
|
|
|
|
| ||||
|
| -0,5 | 0,0000 |
| -0,5 | 0,00000 |
| 0,05 | 0,0371 | |
|
| -0,4 | -0,1203 |
| -0,45 | -0,0946 |
| 0,10 | 0,0772 | |
|
| -0,3 | -0,1303 |
| -0,40 | -0,1203 |
| 0,15 | 0,1200 | |
|
| -0,2 | -0,1081 |
| -0,35 | -0,1304 |
| 0,20 | 0,1652 | |
|
| -0,1 | -0,630 |
| -0,30 | -0,1303 |
| 0,25 | 0,2122 | |
|
| 0 | 0,0000 |
| -0,25 | -0,1204 |
| 0,30 | 0,2607 | |
|
| 0,1 | 0,0772 |
| -0,20 | -0,1081 |
| 0,35 | 0,3103 | |
|
| 0,2 | 0,1652 |
| -0,15 | -0,0881 |
| 0,40 | 0,3610 | |
|
| 0,3 | 0,2607 |
| -0,10 | -0,0630 |
| 0,45 | 0,4121 | |
|
| 0,4 | 0,36098 |
| -0,05 | -0,0335 |
| 0,50 | 0,4637 | |
|
| 0,5 | 0,46365 |
| 0,00 | 0,0000 |
Отже,
![]() .
.
Нехай деяка функція f(x) задана в вузлах інтерполяції:
(i=1,2,3.,n) на відрізку [а,b] таблицею значень: ![]() .
.
Потрібно знайти значення інтегралу 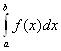 .
.
Спершу складемо інтерполяційний багаточлен Лагранжа:
![]()
Для рівновіддалених вузлів інтерполяційний багаточлен має вигляд:
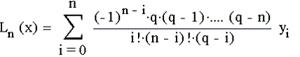
де q=(x-x0) /h – крок інтерполяції, замінимо підінтегральну функцію f(x) інтерполяційним багаточленом Лагранжа:
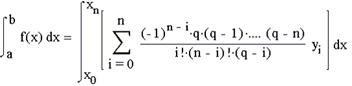
Поміняємо знак підсумовування і інтеграл і винесемо за знак інтеграла постійні елементи:
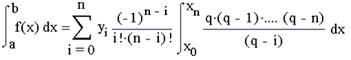
Оскільки dp=dx/h, то, замінивши межі інтеграції, маємо:
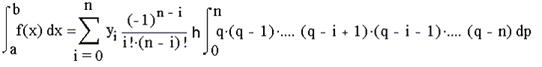
Для рівновіддалених вузлів інтерполяції на відрізку [а,b] величина крок визначається як h=(b-a)/n. Представивши цей вираз для h у формулу (4) і виносячи (b-a) за знак суми, отримаємо:
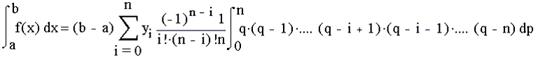
Покладемо, що
![]()
де i=0,1,2.,n; Числа ![]() називають коефіцієнтами Ньютона-Kотеса. Ці коефіцієнти не залежать від вигляду f(x), а є функцією тільки по n. Тому їх можна обчислити заздалегідь. Остаточна формула виглядає так:
називають коефіцієнтами Ньютона-Kотеса. Ці коефіцієнти не залежать від вигляду f(x), а є функцією тільки по n. Тому їх можна обчислити заздалегідь. Остаточна формула виглядає так:
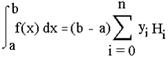
Формула трьох восьмих:
Якщо в формулі Ньютона-Котеса взяти n = 3, тобто функцію f(x) замінити інтерполяційним багаточленом третього степеня, побудованим за значення функції f(x) у точках x0=a, x1=a+h, x2=a+2h, x3=b, h=(b-a )/3. то одержимо таку квадратурну формулу:
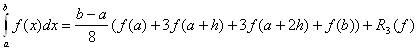 де
де
![]()
Ця квадратурна формула називається малою квадратурною формулою трьох восьмих. Використовуючи цю формулу, легко записати велику квадратурну формулу трьох восьмих.
Завдання
Обчислити інтеграл методом прямокутників, трапецій, парабол, трьох восьмих, Монте-Карло оцінити абсолютну та відносну похибку обчислення :А) заданий інтеграл обчислити наближено та точно.
B) заданий інтеграл обчислити наближено.
Варіант 1
1. ![]()
2. ![]()
3. 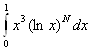
Варіант 2
1. ![]()
2. ![]()
3. 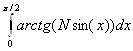
Варіант 3
1. ![]()
2. ![]()
3. 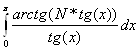
Варіант 4
1. ![]()
2. ![]()
3. 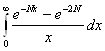
Варіант 5
1. ![]()
2. ![]()
3. 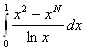
Варіант 6
1. ![]()
2. ![]()
3. 
Варіант 7
1. ![]()
2. ![]()
3. 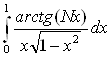
Варіант 8
1. ![]()
2. ![]()
3. 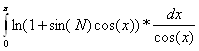
Варіант 9
1. ![]()
2. ![]()
3. ![]()
Варіант 10
1. ![]()
2. ![]()
3. 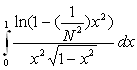
Рекомендована література:
1. Цегелик Г.Г. Чисельні методи: Підручник. – Львів: Видавничий центр ЛНУ ім. І. Франка, 2004. – 408 с.
2. Коссак О., Тумашова О., Коссак О. Методи наближених обчислень: Навч. посіб. – Львів: Бак, 2003. – 168 с.
3. Анджейчак І.А., Федю Є.М., Анохін В.Є. і ін. Практикум з обчислювальної математики. Основні числові методи. Частина І. – Навч. посіб. Львів: Вид-во ДУ «Львівська політехніка», 2000. – 100 с.
4. Дудикевич А.Т., Левицька С.М., Шахно С.М. Практична реалізація методів розв’язування нелінійних рівнянь і систем: Навч.-метод. посібн. – Львів: ВЦ ЛНУ ім.. І.Франка, 2007. – 78 с.
5. Паранчук Я.С. та ін. Алгоритмізація, програмування, числові та символьні обчислення в пакеті MathCAD. – Навч. посіб. / Я.С. Паранчук, А.В. Маляр, Р.Я. Паранчук, І.Р. Головач. – Львів: Вид-во Львівської політехніки, 2008. – 164 с.
Похожие работы
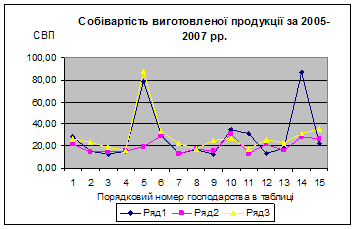
... і над плановим. Відомо, що собівартість є одним з головних джерел резервів підвищення ефективності роботи підприємства. Звідси сформуємо мету і задачі даної роботи. Метою даної роботи є підвищення ефективності роботи підприємства ВАТ «Дніпрополімермаш» шляхом управління собівартістю продукції. Відповідно, для досягнення поставленої мети необхідно вирішити наступні задачі: 1. Проаналізувати ...
... частки можна прийняти . 5. Похибки степеня. Нехай А = (х + ∆ х)т , и = хт , де т – натуральне число, х > 0. Використовуючи похибки добутку, одержуємо |∆u| < mxm - 1|∆x|, δ ≤ mδ1, де δ – відносна похибка степеня; δ1 – відносна похибка аргументу х. Тому за граничні абсолютну та відносну похибки степеня можемо прийняти ∆u= mx
... общин, де кожний буде зобов'язаний трудитися. М.А. Бакунін дотримувався ідей анархізму, бачивши у владі причину експлуатації. Один з феноменів російської науки - плідна розробка ідей економіко-математичного моделювання, заснована на базі як „чистих” математиків, що направили свої зусилля в економіку, так і розробок професійних економістів. Перші російські економісти-математики (Ю.Г. Жуковській, ...
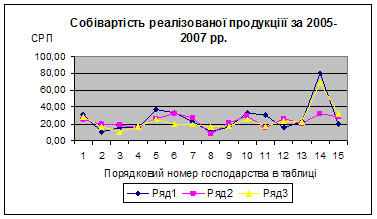
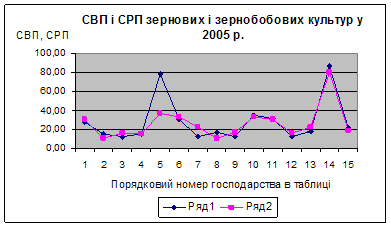
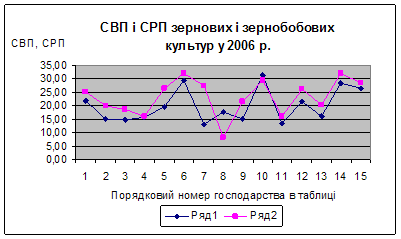
... змін, спостерігається тільки нестабільність та по деяких господарствах різкі зміни собівартості продукції, що виготовляється та реалізується. 3. Економіко-математичне моделювання в управлінні підприємством 3.1 Економіко-математичне моделювання урожайності сільськогосподарської продукції методом Брандона. Нехай економіко-математична модель матиме вид: , Де =; =; = ; Y - ...

0 комментариев