Навигация
3. Функция риска
доверительный интервал вероятность статистическая гипотеза
Пусть имеются две противоположные гипотезы Но и Н1 и некоторая связанная с ними случайная величина Y. И пусть у - значение случайной величины Y, полученное в результате испытаний, которое принадлежит множеству D - множество всех значений случайной величины Y. Требуется провести проверку гипотезы Но относительно конкурирующей гипотезы Н1 на основании результатов испытания.
Разобьем множество D на две части - Dо и D1 с условием принятия гипотезы Но при попадании полученного значения у в Dо и гипотезы Н1 - при попадании у в D1. Выбор решающего правила, то есть разбиение множества Dна две части Dо и D1 в любой задаче проверки гипотез возможен больше, чем одним способом. Возникает вопрос, какое из этих разбиений в каждой конкретной задаче считать наилучшим? Чтобы решить поставленную задачу нужно обладать некоторой дополнительной информацией. Такая информация носит название априорной.
Будем считать известными два условных распределения вероятностей случайной величины Y:
- плотность распределения случайной величині Y при условии, что верна гипотеза Но;
- плотность распределения случайной величині Y при условии, что верна гипотеза Н1;
Кроме того нам потребуется априорная вероятность р того, что гипотеза Но имеет место.
Введем в рассмотрение события:
А – верна гипотеза Но, тогда р = р(А);
– верна конкурирующая гипотеза Н1, тогда р() = 1 - р;
В – в результате эксперимента значение у попало в интервал Dо;
– в результате эксперимента значение у попало в интервал D1.
Тогда по результатам эксперимента возможны только четыре события:
АВ – верна гипотеза Но и принято решение о ее истинности;
В – верна гипотеза Н1, а принято решение о истинности гипотезы Но;
А – верна гипотеза Но, а принято решение о истинности гипотезы Н1;
– верна гипотеза Н1 и принято решение о ее истинности.
Ясно, что события В и А определяют ошибочные решения. Событию В соответствует так называемая ошибка первого рода, а событию А - ошибка второго рода.
Для ответа на вопрос, какое из решающих правил следует считать лучшим, введем понятие функции потерь и функцию риска.
Функция потерь – дискретная случайная величина С, которая каждому из событий АВ, В, А, ставит в соответствие потери 
, выраженные в каких-то единицах. Правильному решению естественно положить нулевые потери, а ошибкам первого и второго ряда положить соответственно положительные потери (числа) С1 и С2, которые нужно задать.
Пусть ро = р(АВ или ), р1 = р(В), р2 = р(А). Определение значений этих вероятностей будет проведено ниже. Ряд распределения для случайной величины С имеет вид
| С | 0 | с1 | с2 |
| р | ро | р1 | р2 |
Определение. Математическое ожидание М(С) случайной величины С называется функцией риска и обозначается буквой r.
Таким образом, r = М(С) = 0 ро + с1 р1 + с2 р2 = с1 р1 + с2 р2.
Введение функции риска приводит к естественному выбору решающего правила. Из двух правил лучшим считается то, которое приводит к меньшему риску. Для нахождения минимума функции риска найдем вероятности р1 и р2:
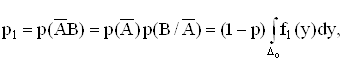
Тогда
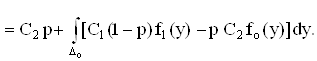
Для того, чтобы интеграл был минимальным, а значит и минимальное значение принимала функция риска r, нужно в состав Dо включить только те у, в которых подыинтегральная функция
С1 (1-р) f1(y) – p C2 fo(y) < 0,
а в состав D1- остальные значения у.
Последнее неравенство можно записать в виде
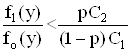
Функция f1(y)/fo(y) называется отношением правдоподобия.
Итак, оптимальное решающее правило заключается в следующем: полученное в результате эксперимента значение у подставляется в отношение правдоподобия f1(y)/fo(y) и сравнивается с числом
l =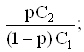 
если полученное в результате вычисления число f1(y)/fo(y) меньше l, принимается гипотеза Но; в противном случае – гипотеза Н1.
Величина l носит название порога, а оптимальное решающее правило носит название порогового критерия оптимальности.
Похожие работы
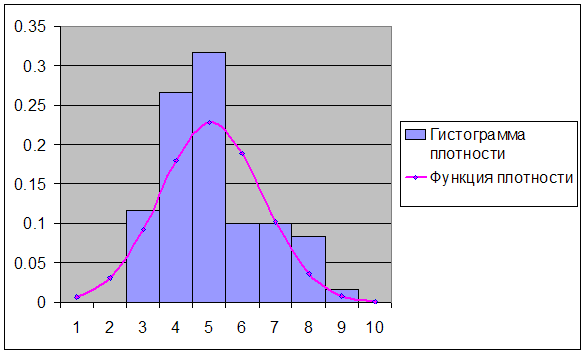
... критических точек распределения ([1], стр. 465), по уровню значимости =0,05 и числу степеней свободы 8-3=5 находим Т.к. , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины . Для случайной величины : Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле , где - объем выборки, - шаг (разность между ...
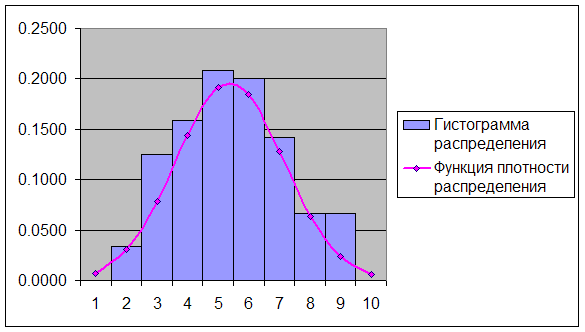
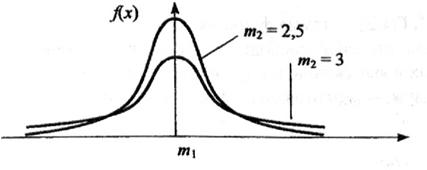
... u0, u1, …, uk взаимно независимые нормально распределенные случайные величины с нулевым средним и конечной дисперсией. Аргумент t не зависит от дисперсии слагаемых. Функция плотности распределения Стьюдента статистический гипотеза математический ожидание Величина k характеризует количество степеней свободы. Плотность распределения – унимодальная и симметричная функция, похожая на нормальное ...
... данных и по внедрению накопленного арсенала современных методов прикладной статистики. По нашему мнению, широкого внедрения заслуживают, в частности, методы многомерного статистического анализа, планирования эксперимента, статистики объектов нечисловой природы. Очевидно, рассматриваемые работы должны быть плановыми, организационно оформленными, проводиться мощными самостоятельными организациями и ...
... и изучают их. Таким образом, выборочной совокупностью или просто выборкой объёма n будем называть совокупность n объектов, отобранных из интересующей нас генеральной совокупности. 2. Статистическая оценка законов распределения Если выборка объёма n из генеральной совокупности представительна, то элементы с одинаковыми значениями варианты будут приблизительно одинаково часто встречаться ...
0 комментариев