Навигация
РЕГУЛЯРИЗАЦИЯ ФОРМУЛ ОБРАЩЕНИЯ
24944
знака
1
таблица
16
изображений
5. РЕГУЛЯРИЗАЦИЯ ФОРМУЛ ОБРАЩЕНИЯ
Обычно вместо точной проекции 
известна искаженная проекция
, (5.1)
где 
описывает соответствующую случайную погрешность,
проявляющуюся в данном случае в виде аддитивной добавки. Тогда задачу реконструкции можно переформулировать следующим образом: требуется по приближенным проекционным данным найти приближенную функцию 
, которая в каком-то смысле хорошо описывала бы искомую функцию 
. Непосредственная подстановка "зашумленных" проекционных данных [7] в указанный вычислительный алгоритм приводит к большим искажениям в . Дело в том, что задача реконструкции относится к так называемым некорректным задачам [8]. Физическая суть "некорректности" проявляется в том, что если пользоваться точным решением некорректной задачи, то даже при небольших искажениях в исходных данных это решение может существенно отличатся от искомой функции . Устранить это нежелательное явление можно, регуляризируя формулы обращения. В методах, основанных на преобразовании Радона (раздел 2) для этого достаточно "подавить" влияние высоких частот в 
, что можно, например, достичь умножением 
на регуляризующие функции 
. Обычно регуляризующие функции выбирают в следующем виде:
; (5.2)
; (5.3)
(5.4)
Постоянная 
называется параметром регуляризации и подбирается эмпирически при расчете. Чем больше интенсивность ожидаемых искажений, тем больше должно быть значение параметра .
Формулы обращения преобразования Радона (2.25) с учетом регуляризации получаются путем замены 
на 
, а (2.32) такой же заменой в (2.29).
Что касается метода ортогональных полиномов (раздел 4), то описанный выше алгоритм реконструкции функции является точным в том смысле, что если ее радоновский образ известен точно, то по нему, в принципе, можно найти точные значения всех коэффициентов 
и далее по формуле (4.6) осуществить точное восстановление искомой функции. Однако на практике реализовать подобное точное восстановление невозможно. Этому препятствуют, по крайней мере, две причины. Первая кроется в самой сущности обсуждаемого алгоритма, ибо, для того чтобы он был точным, необходимо согласно (4.6) в общем случае определить бесконечное число членов . Вторая связана с невозможностью точного измерения радоновского образа. В результате определяемые по нему коэффициенты 
будут отличаться от их точных значений .
Таким образом, в реальном алгоритме восстановления участвует ограниченное число членов ряда (4.6). Для определенности в дальнейшем будем считать, что ограничение проводится по индексу 
, так что 
. Этого условия достаточно, так как в силу (4.7) оно однозначно определяет конечное число всех отличных от нуля коэффициентов . Изменяя порядок суммирования в (4.6) и делая его аналогичным (4.10), имеем
. (5.11)
Известно [5], что ограничение суммирования в (5.1) приводит к функции 
, хотя и отличной от , но это отличие, оцениваемое по среднеквадратической погрешности
, (5.12)
будет минимально, если коэффициенты в (4.1) рассчитываются по прежним формулам (4.2). Данный факт говорит о том, что вынужденное на практике ограничение числа определяемых коэффициентов не должно привести к изменению тех формул, по которым они рассчитываются.
С увеличением числа 
- членов суммы (5.11) погрешность (5.12) монотонно уменьшается. Важно подчеркнуть, что это происходит только тогда, когда коэффициенты известны точно. Если же они определяются с некоторыми ошибками, то отмеченная зависимость нарушается. В этом случае конкретный характер поведения погрешности (5.12) с ростом числа М во многом определяется статистикой ошибок измерения. В результате уменьшение усредненной погрешности за счет увеличения числа членов суммы (5.11) может происходить только до некоторого предела, после которого она начинает увеличиваться. Более того, часто при бесконечном увеличении числа слагаемых погрешность стремится к бесконечности. Таким образом, вторая причина, связанная с неточностью определения коэффициентов , так же, как и первая, приводит к необходимости использовать при восстановлении ограниченное число членов ряда (5.1), но в отличие от первой она указывает на то, что это ограничение возможно осуществить оптимальным образом. В данном случае не требуется регуляризации в том виде, в каком она была введена ранее. Ее роль как «сознательного ограничителя точности в идеальных условиях» будет выполнять «сознательное», оптимальное ограничение числа членов аппроксимирующих полиномов для данного уровня шумовых флуктуаций.
ЛИТЕРАТУРА
1. Гельфанд, И.М. Интегральная геометрия и связанные с ней вопросы теории представлений [Текст]: монография / И.М Гельфанд, М.И. Граев, Н.Я. Виленкин. - М.: Физматгиз, 1962. - 656 с.
2. Календер, В. Компьютерная томография. Основы, техника, качество изображения и области клинического использования [Текст]: монография / В. Календер. - М.: Техносфера, 2006, -344 с.
3. Терещенко С.А. Методы вычислительной томографии [Текст]: монография /С.А.Терещенко. – М.: Физматлит, 2004. - 319 с.
4. Наттерер Ф. Математические аспекты компьютерной томографии: Пер. с англ. [Текст]: монография /Ф. Наттерер. -М.: Мир, 1990.-288 с.
5. Хелгасон, С. Преобразование Радона: Пер. с англ. [Текст]: монография / С. Хелгасон. - М.: Мир, 1983. - 152 с.
6. Хермен, Г. Восстановление изображений по проекциям: основы реконструктивной томографии: Пер. с англ. [Текст]: монография / Г. Хермен. - М.: Мир, 1983. - 349 с.
7. Троицкий, И.Н. Статистическая теория томографии [Текст]: монография / И.Н.Троицкий. – М.: Радио и связь, 1989. - 240 с.
8. Тихонов, А.Н. Методы решения некорректных задач. [Текст]: монография / А.Н. Тихонов, В.Я. Арсенин. - М.:Наука, 1986. - 287 с.
9. Гельфанд, И.М. Обобщенные функции и действия над ними [Текст]: монография / И.М. Гельфанд, Г.Е. Шилов. - М.: Физматгиз, 1959. - 497 с.
ПРИЛОЖЕНИЕ А
Чтобы вычислить (2.9), воспользуемся соотношением [9]
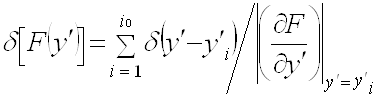, (A1)
где 
- простые корни уравнения 
, 
- их число.
Пусть 
. Тогда
, 
, 
,
так что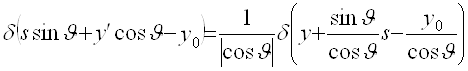 
. Подстановка (А1) в (2.9) дает
=
=
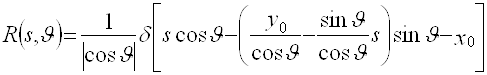, (А2)
где при переходе к последнему равенству было учтено, что 
.
ПРИЛОЖЕНИЕ Б
Убедиться в справедливости (2.24) можно, если воспользоваться (2.8) и под интеграл в (2.17) вместо подставить 
, затем сделать замену переменных 
.
Похожие работы
... технологических операций (они реализованы в соответствующих блоках программного комплекса): Построение математической модели. Преобразование математической модели. Планирование вычислительного эксперимента. Построение программной реализации математической модели Отладка и тестирование программной реализации. Проведение вычислительного эксперимента. Документирование эксперимента. ...
... часть пульта управления (или устройства вывода данных) оператора-рентгенолога. Аналогичные пульты управления можно применять и в других системах получения изображения, например на основе ядерного магнитного резонанса или компьютерной томографии. Цифровое изображение можно записать на магнитном носителе, оптическом диске или же на специальном записывающем устройстве, способном постоянно вести ...
... томография Спиральная КТ используется в клинической практике с 1988 года, когда компания Siemens Medical Systems представила первый спиральный компьютерный томограф. Спиральное сканирование заключается в одновременном выполнении двух действий: непрерывного вращения источника – рентгеновской трубки, генерирующей излучение, вокруг тела пациента, и непрерывного поступательного движения стола с ...
... вещества в участках избыточной васкуляризации. Часто отмечается ускоренный переход контрастного вещества в венозные пути оттока. 3. Компьютерная томография Компьютерная томография - принципиально новый и универсальный метод рентгенологического исследования. С ее помощью можно изучать все части тела, все органы, судить о положении, форме, величине, состоянии поверхности и структуре органа, ...
0 комментариев