Навигация
За знайденими l, k обчислити нові значення елементів таблиці за формулами
3. за знайденими l, k обчислити нові значення елементів таблиці за формулами
4.
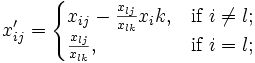 (12)
(12)
![]() ,
,
де ![]() та перейти до виконання операції (1) з новими значеннями всіх xij = x'ij.
та перейти до виконання операції (1) з новими значеннями всіх xij = x'ij.
Перетворення (12) замінює вектор коефіцієнтів Xk = (x1k, …, xmk) на одиничний вектор Xk з xlk = 1. В силу монотонного збільшення x0 повернення до вже пройденого плану неможливе, а із скінченності кількості опорних планів випливає скінченність алгоритму.
Початковий опорний план з одиничним базисом можна отримати, розв'язавши описаним алгоритмом допоміжну задачу
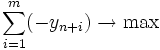 ,
,
при обмеженнях
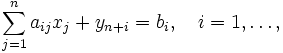
![]() ;
;
![]() ,
,
яка містить одиничний базис, який складається із векторів An+1, …, An+m. Цим векторам відповідають штучні змінні із значеннями ![]() , i = 1, …, m. Якщо в оптимальному розв'язку цієї задачі
, i = 1, …, m. Якщо в оптимальному розв'язку цієї задачі 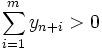 , вихідна задача не має розв'язку. Якщо ж
, вихідна задача не має розв'язку. Якщо ж 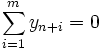 та задача невироджена, оптимальний базис складається лише тільки із векторів вихідної задачі, які за формулами (12) перетворені в одиничну матрицю. Якщо задача має невироджені плани, значення z0 може не збільшуватись на ряді ітерацій. Це відбувається через те, що значення відповідних
та задача невироджена, оптимальний базис складається лише тільки із векторів вихідної задачі, які за формулами (12) перетворені в одиничну матрицю. Якщо задача має невироджені плани, значення z0 може не збільшуватись на ряді ітерацій. Це відбувається через те, що значення відповідних ![]() дорівнює нулю та визначається неоднозначно. В таких випадках монотонність методу порушується і може трапитись зациклювання, тобто, повернення до вже пройденого базису. Невелика зміна вектора обмежень задачі, яка полягає в заміні величин bi на bi + εi, де εi достатньо малі, при вдалому виборі εi не змінюють множину векторів оптимального опорного плану вихідної задачі і робить її невиродженою.
дорівнює нулю та визначається неоднозначно. В таких випадках монотонність методу порушується і може трапитись зациклювання, тобто, повернення до вже пройденого базису. Невелика зміна вектора обмежень задачі, яка полягає в заміні величин bi на bi + εi, де εi достатньо малі, при вдалому виборі εi не змінюють множину векторів оптимального опорного плану вихідної задачі і робить її невиродженою.
Описаний вище алгоритм називається першим (або прямим) алгоритмом симплекс-методу. Також відомий другий алгоритм (алгоритм із оберненою матрицею). В ньому перетворюється лише матриця A-1, обернена до базисної матриці.
3. Прикладний розділ
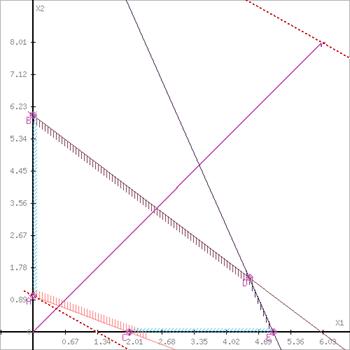
3.1 Вирішення задачі лінійного програмування симплекс-методом
Для розробки математичної моделі задачі позначимо:
x1 – кількість продукту А;
x2 – кількість продукту В;
Цільова функція буде мати вид:
Z=x1+2x2¦mах
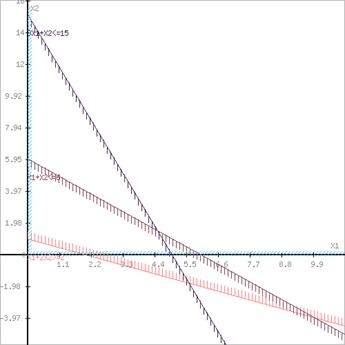
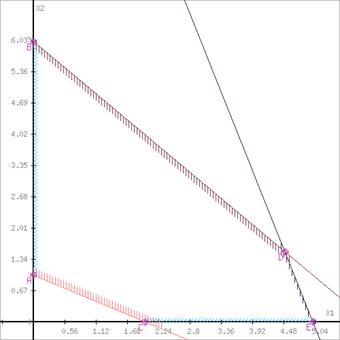
Система обмежень:
3 x1+3 x2 <= 15 2 x1+6 x2 <= 18 4 x1<= 16 x1+2x2 <= 8 Xj>=0, j=1..2
Зведення задачі до канонічного виду: Zmax = x1+2x2 при умовах:
3x1+3x2+x3 = 15 2x1+6x2+x4 = 18 4x1+x5 = 16 x1+2x2+x6 = 8 Xj>=0, j=1..6
Таблиця 5.
| Базис | С | План | 1 | 2 | 0 | 0 | 0 | 0 |
| X3 | 0 | 15 | 3 | 3 | 1 | 0 | 0 | 0 |
| X4 | 0 | 18 | 2 | 6 | 0 | 1 | 0 | 0 |
| X5 | 0 | 16 | 4 | 0 | 0 | 0 | 1 | 0 |
| X6 | 0 | 8 | 1 | 2 | 0 | 0 | 0 | 1 |
| Zj-Cj | 0 | -1 | -2 | 0 | 0 | 0 | 0 |
Таблиця 6.
| Базис | С | План | 1 | 2 | 0 | 0 | 0 | 0 |
| X3 | 0 | 6 | 2 | 0 | 1 | -0,5 | 0 | 0 |
| X2 | 2 | 3 | 40238 | 1 | 0 | 40330 | 0 | 0 |
| X5 | 0 | 16 | 4 | 0 | 0 | 0 | 1 | 0 |
| X6 | 0 | 2 | 40238 | 0 | 0 | -0,3333 | 0 | 1 |
| Zj-Cj | 6 | -0,3333 | 0 | 0 | 40238 | 0 | 0 |
Таблиця 7.
| Базис | С | План | 1 | 2 | 0 | 0 | 0 | 0 |
| X1 | 1 | 3 | 1 | 0 | 40210 | -0,25 | 0 | 0 |
| X2 | 2 | 2 | 0 | 1 | -0,1667 | 40269 | 0 | 0 |
| X5 | 0 | 4 | 0 | 0 | -2 | 1 | 1 | 0 |
| X6 | 0 | 1 | 0 | 0 | -0,1667 | -0,25 | 0 | 1 |
| Zj-Cj | 7 | 0 | 0 | 40330 | 40269 | 0 | 0 |
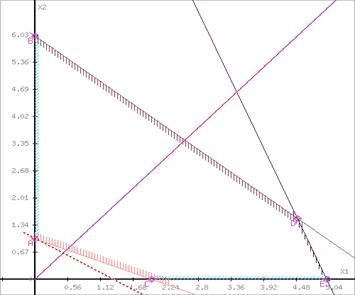
Відповідь: Zmax =7, Xопт =(3 ; 2 ; 0 ; 0 ; 4 ; 1).
Це свідчить про те, що максимальний прибуток підприємства буде дорівнювати 7 грн., а виробництво продукції А і В складає відповідно 3 і 2 одиниці.
Похожие работы
... програмування та її економіко – математичної моделі, опис функцій і команд у вирішенні задач лінійного програмування засобами Exel, а також рішення конкретної задачі за допомогою ПК. 1. Побудова економіко–математичної моделі Загальна модель задачі математичного програмування має такий вигляд: У структурі моделі (1.1) можна виділити 3 елементи: 1) Набір керованих змінних x1, x2, ... x ...
... і (усі сj’ ≥0), але не задовільняє критерії допуску (не всі ві ≥0). Варіант симплекс метода, який приміняється для рішення таких задач, називається двоїстим симплекс методом. За його допомоги рішаються задачі лінійного програмування виду: (4.3.1) де система обмежень має такий вигляд і всі приведені коефіцієнти цільової функції сj’ ≥0, і=1,n. При цьому умова ві ≥0, ...
2х1+5х2 + 15х3+ 10х4 досягає максимуму при системі обмежень: Розв'язуємо задачу лінійного програмування симплексним методом. Введемо балансні змінні х5 ≥ 0, х6≥ 0, х7≥ 0. Їх величина поки що невідома, але така, що перетворює відповідну нерівність у точну рівність. Після цього, задача лінійного програмування набуде вигляду: ∫ = 12х1+5х2 + 15х3+ 10х4 → max при ...
... – відпускна ціна i-го заводу j-й продукції; - закупівельна ціна i-го заводу j-й продукції, - шуканий обсяг закупівель на i-м заводі j-й продукції. 2.5 Перевірка моделі оптимізації на контрольному прикладі В цьому підрозділі на прикладі підприємства ТОВ "Гермес-Груп" розрахуємо модель (2.4.5) за допомогою електроних таблиць MSEcxel. Цільова функція має вигляд: де - об’єм закупівлі; ...
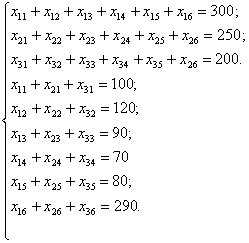


0 комментариев