Навигация
Моделювання і методика рішення задач лінійного програмування
2. Моделювання і методика рішення задач лінійного програмування
2.1 Різновиди форм моделі задач лінійного програмування
2.1.1 Загальна форма моделіЗагальна форма моделі задачі лінійного програмування характеризується наступним:
Знайти сукупність значень n змінних ![]() що задовольняють системі обмежень:
що задовольняють системі обмежень:
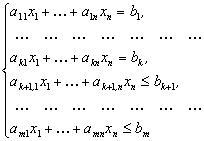
і умові невід’ємності:
![]() ,
,
для яких лінійна функція (цільова функція) ![]() досягає екстремуму (максимуму або мінімуму) [9].
досягає екстремуму (максимуму або мінімуму) [9].
Знайти сукупність значень n змінних ![]() що задовольняють системі обмежень:
що задовольняють системі обмежень:
![]()
![]()
і умові невід’ємності:
![]()
![]() ,
,
для яких лінійна функція (цільова функція) ![]() досягає максимуму.
досягає максимуму.
Якщо ввести у розгляд матрицю:
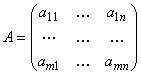
і вектори:
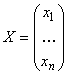 ,
, 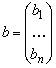 ,
, ![]() ,
,
то стандартна форма моделі матиме вид:
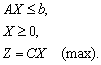
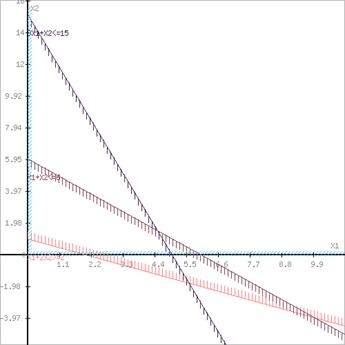
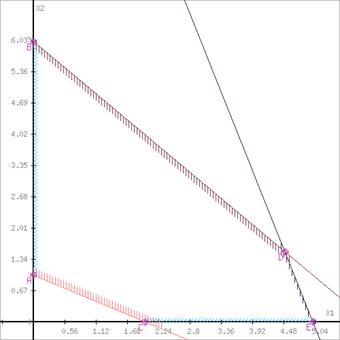
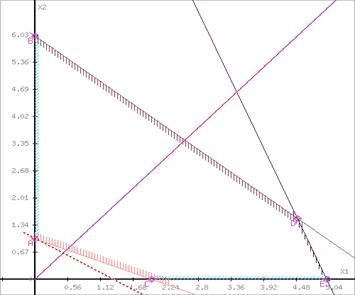
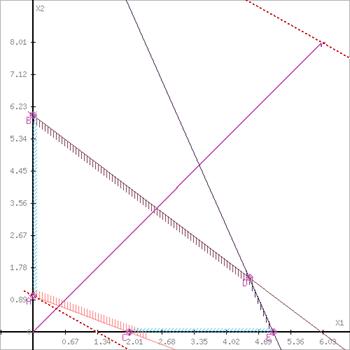
Задачу ЛП в стандартній формі зручно вирішувати графічним методом, якщо число змінних дорівнює двом (![]() ) [1].
) [1].
2.1.3 Канонічна форма моделі
Знайти сукупність значень n змінних ![]() що задовольняють системі рівнянь:
що задовольняють системі рівнянь:
 (
(![]() )
)
і умові невід’ємності:
![]() (
(![]() ),
),
для яких цільова функція ![]() досягає максимуму.
досягає максимуму.
Компактна форма моделі має вид:
![]() ,
,
![]() ,
,
![]() . [9].
. [9].
2.2 Симплекс-метод
Симплекс-метод — метод розв'язання задачі лінійного програмування, в якому здійснюється скерований рух по опорних планах до знаходження оптимального розв'язку; симплекс-метод також називають методом поступового покращення плану [6].
Опишемо метод.
Нехай невироджену задачу лінійного програмування представлено в канонічному вигляді:
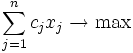 ,
,
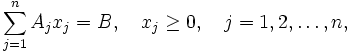
де X = (x1, …, xn) — вектор змінних,
C = (c1, …., cn), B = (b1, …, bm)T,
Aj = (a1j, …, amj)T, j = 1, …, n — задані вектори,
T — знак транспонування, та
![]()
відмінні від нуля компоненти опорного плану, для полегшення пояснення розташовані на перших m місцях вектору X. Базис цього плану — ![]() . Тоді
. Тоді
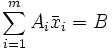 , (1)
, (1)
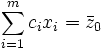 , (2)
, (2)
де ![]() значення лінійної форми на даному плані. Так як вектор-стовпці матриці A лінійно незалежні, будь який із векторів умов Aj розкладається по них єдиним чином:
значення лінійної форми на даному плані. Так як вектор-стовпці матриці A лінійно незалежні, будь який із векторів умов Aj розкладається по них єдиним чином:
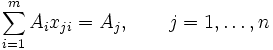 , (3)
, (3)
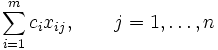 , (4)
, (4)
де xij коефіцієнт розкладання. Система умов
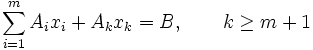 , (5)
, (5)
zk ≥ 0, xj = 0, j = m + 1, …, n, j ≠ k (6)
при заданому k визначає в просторі змінних задачі промінь, який виходить із точки, яка відповідає опорному плану, що розглядається. Нехай значення змінної xk при русі по цьому променю дорівнює θ, тоді значення базисних змінних дорівнюють xi(θ). В цих позначеннях рівняння (5) можна представити в виді
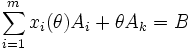 . (7)
. (7)
помноживши рівняння (3) на θ при j = k та віднявши від рівняння (1), отримаємо
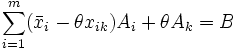 . (8)
. (8)
Із рівнянь (7-8) отримаємо
![]() . (9)
. (9)
Оскільки xi(θ) при θ = 0 визначають план задачі, то найбільше θ, яке не порушує обмеження xi (θ) ≥ 0, визначається із умови
![]() . (10)
. (10)
де I = {i | xik > 0}.
В силу невиродженості задачі мінімум досягається не більш ніж для одного i = J та θ > 0. Значення лінійної форми при θ = θ0 визначається із рівнянь (9), (4), (2)
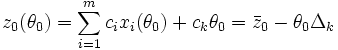 ,
,
де Δk = zk — ck. Очевидно, Δj = 0 для j = 1, …, m.
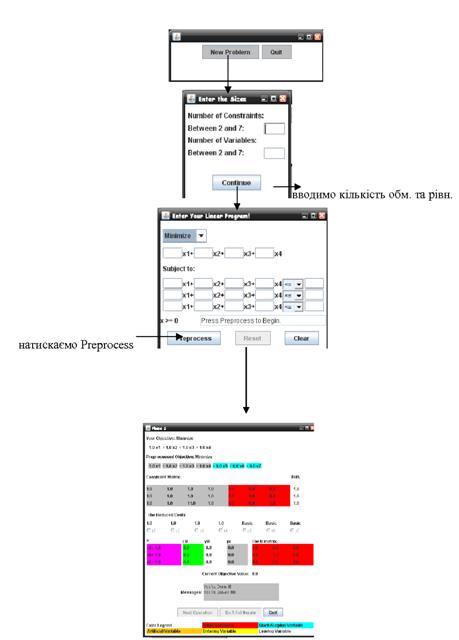
Нехай ![]() — початковий базис із m одиничних векторів. Всі дані задачі записуються у вигляді симплекс-таблиці (першої ітерації обчислювального процесу). Симплекс-алгоритм розв'язання задачі лінійного програмування складається із наступних операцій:
— початковий базис із m одиничних векторів. Всі дані задачі записуються у вигляді симплекс-таблиці (першої ітерації обчислювального процесу). Симплекс-алгоритм розв'язання задачі лінійного програмування складається із наступних операцій:
1. знайти Δk = minjΔj. Якщо Δk = 0, тоді план, який розглядається оптимізовано; якщо Δk < 0, вектор Ak вводиться в базис;
2. знайти θ0 та l, для якого ![]() , із формули (10). Якщо I = Λ — порожня множина, лінійна форма необмежена зверху; якщо I ≠ Λ вектор Al виводиться із базису;
, із формули (10). Якщо I = Λ — порожня множина, лінійна форма необмежена зверху; якщо I ≠ Λ вектор Al виводиться із базису;
Похожие работы
... програмування та її економіко – математичної моделі, опис функцій і команд у вирішенні задач лінійного програмування засобами Exel, а також рішення конкретної задачі за допомогою ПК. 1. Побудова економіко–математичної моделі Загальна модель задачі математичного програмування має такий вигляд: У структурі моделі (1.1) можна виділити 3 елементи: 1) Набір керованих змінних x1, x2, ... x ...
... і (усі сj’ ≥0), але не задовільняє критерії допуску (не всі ві ≥0). Варіант симплекс метода, який приміняється для рішення таких задач, називається двоїстим симплекс методом. За його допомоги рішаються задачі лінійного програмування виду: (4.3.1) де система обмежень має такий вигляд і всі приведені коефіцієнти цільової функції сj’ ≥0, і=1,n. При цьому умова ві ≥0, ...
2х1+5х2 + 15х3+ 10х4 досягає максимуму при системі обмежень: Розв'язуємо задачу лінійного програмування симплексним методом. Введемо балансні змінні х5 ≥ 0, х6≥ 0, х7≥ 0. Їх величина поки що невідома, але така, що перетворює відповідну нерівність у точну рівність. Після цього, задача лінійного програмування набуде вигляду: ∫ = 12х1+5х2 + 15х3+ 10х4 → max при ...
... – відпускна ціна i-го заводу j-й продукції; - закупівельна ціна i-го заводу j-й продукції, - шуканий обсяг закупівель на i-м заводі j-й продукції. 2.5 Перевірка моделі оптимізації на контрольному прикладі В цьому підрозділі на прикладі підприємства ТОВ "Гермес-Груп" розрахуємо модель (2.4.5) за допомогою електроних таблиць MSEcxel. Цільова функція має вигляд: де - об’єм закупівлі; ...
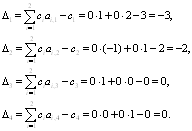


0 комментариев