Расчет разрядности представления данных и числа итераций

1.1 Расчет разрядности представления данных и числа итераций

Произведём расчёт числа итераций и разрядности в математическом пакете SciLab.

Определим диапазон допустимых значений заданных элементарных функций. Исследуем итерационные формулы для вычисления Θ = arcth Z:

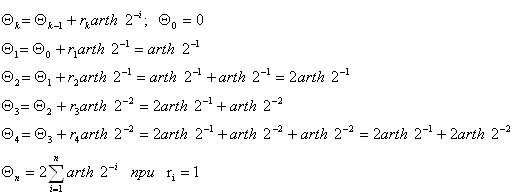
Тогда границы значений функции, при которых метод Волдера является верным, лежит в следующем пределе:

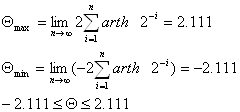
При этом Z для функции Θ = arch Z должно находиться в следующем диапазоне:

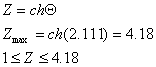
Определим диапазон допустимых значений аргументов функции 2^Z, а затем диапазон значений само функции.

 

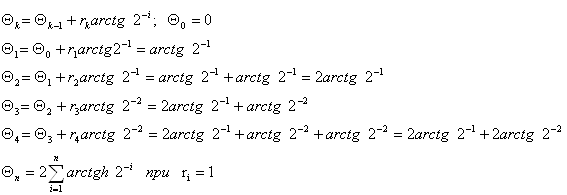
Тогда границы значений функции, при которых метод Волдера является верным, лежит в следующем пределе:

Следовательно функция будет изменяться в диапазоне:

.

Рассчитаем минимальное число итераций при погрешности преобразования равной 0,01% и максимальной выходной величине 4,685:

Тогда количестово разрядов данных составит:

.

 

1.2 Разработка итерационных алгоритмов вычисления функции в математическом пакете SciLab

Промоделируем в пакете математического моделирования MatLab метод Волдера «Цифра за цифрой» для анализа его работоспособности и определения погрешности вычислений.

В цикле подсчитаем значение абсолютной погрешности при изменении количества итераций от 1 до n и при изменении разрядности данных (дробная часть задается от 1 до 16 бит).

Листинг программы для исследования погрешности при изменении числа итераций:

//== function arch ====

//function [archZ] = arch(Z,N)

Q0 = 0;

x0 = 0.6072529;

y0 = 0;

N=20;

Z= 0.512

 acos_ist = asin(Z)

for n=1:N

Q(1)=Q0+atan(2^(-0));

r(1)=sign(Z-y0);

x(1)=x0-y0*2^(-0);

y(1)=y0+x0*2^(-0);

for i=1:n

r(i)=sign(Z-y(i));

// ARTH =atan(2^(-i));

Q(i+1)= Q(i)+r(i)*atan(2^(-i));

x(i+1)= x(i)-r(i)*y(i)*2^(-i);

y(i+1)= y(i)+r(i)*x(i)*2^(-i);

end

arcsinZ(n)= Q(n);

asin_ist = asin(Z);

pogr(n)=(asin_ist-arcsinZ(n))/asin_ist*100;

end

scf(1);

clf();

plot(pogr);

xgrid();

//endfunction

//////////////////////////////////////////////////////////////

Q0 = 0;

x0 = 0.6072529;

y0 = 0;

for n=1:20

m=3;

Q(1)=Q0+atan(2^(-0));

Q(1)=conv(n,m,Q(1));

r(1)=sign(Z-y0);

x(1)=x0-y0*2^(-0);

x(1)=conv(n,m,x(1));

y(1)=y0+x0*2^(-0);

y(1)=conv(n,m,y(1));

for i=1:20

r(i)=sign(Z-y(i));

// ARTH =atan(2^(-i));

Q(i+1)= Q(i)+r(i)*atan(2^(-i));

Q(i+1)=conv(n,m,Q(i+1));

x(i+1)= x(i)-r(i)*y(i)*2^(-i);

x(i+1)=conv(n,m,x(i+1));

y(i+1)= y(i)+r(i)*x(i)*2^(-i);

y(i+1)=conv(n,m,y(i+1));

end

arcsinZ(n)= Q(20);

asin_ist = asin(Z);

pogr(n)=(asin_ist-arcsinZ(n))/asin_ist*100;

end

scf(2);

clf();

plot(pogr);

xgrid();

Запустив приведенную программу, мы получим график зависимости погрешности от числа итераций:

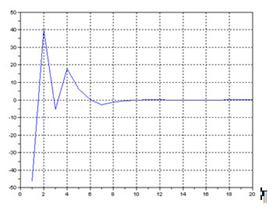
Рис.1.1 - График абсолютной погрешности для функции Θ = arcsin Z при изменяющемся числе итераций

По полученным графикам видно как ведёт себя погрёшность преобразования. При количестве итераций меньше 10 погрешность достигает 5%. По заданию требуется, чтобы погрешность составляла меньше 1%, это достигается при n = 13 и более.

Листинг программы для изменения разрядности данных:

clear

clc

//== function convert real to bin ====

function [x_bin] = conv(n,m,x)

//преобразование целой части

x_int = abs(int(x));

x_tmp=x_int;

for j=1:m

x_tmp = x_tmp/2

if (x_tmp-int(x_tmp))==0

arr_tmp(j)=0

else

arr_tmp(j)=1

x_tmp = int(x_tmp)

end

end

x_cel = 0;

for j=1:m

x_cel = x_cel+arr_tmp(j)*2^(j-1)

end

//преобразование дробной части

x_real = x- x_int;

for i=1:n,

x_real = x_real * 2;

if x_real<1

arr(i)=0;

else

arr(i)=1;

x_real=x_real-1;

end,

x_real1=1-int(x_real)

end

x_new=0;

for i=1:n

x_new=x_new+arr(i)*2^(-i)

end

x_bin=x_cel+x_new

endfunction

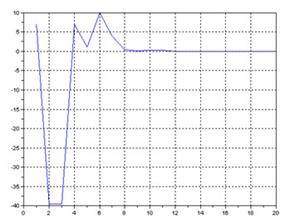
Рис.1.2 - График абсолютной погрешности для функции Θ = arch Z при изменении разрядности дробной части

Изменяя количество бит, приходящихся на дробную часть, исследуется влияние разрядности данных на точность вычислений. Из графика видно, что необходимая точность достигается при разрядности дробной части 13 и более.

Исследуем точность итерационных формул для функции arcth Z в математическом пакете SciLab. Ниже приведен код программы, которая вычисляет погрешность вычисления методом Волдера заданной функции при изменении числа итерации и разрядности дробной части.

 

Листинг программы:

clear

clc

//== function convert real to bin ====

function [x_bin] = conv(n,m,x)

//преобразование целой части

x_int = abs(int(x));

x_tmp=x_int;

for j=1:m

x_tmp = x_tmp/2

if (x_tmp-int(x_tmp))==0

arr_tmp(j)=0

else

arr_tmp(j)=1

x_tmp = int(x_tmp)

end

end

x_cel = 0;

for j=1:m

x_cel = x_cel+arr_tmp(j)*2^(j-1)

end

//преобразование дробной части

x_real = x- x_int;

for i=1:n,

x_real = x_real * 2;

if x_real<1

arr(i)=0;

else

arr(i)=1;

x_real=x_real-1;

end,

x_real1=1-int(x_real)

end

x_new=0;

for i=1:n

x_new=x_new+arr(i)*2^(-i)

end

x_bin=x_cel+x_new

endfunction

//========================================

function [arth_i]=arth(x)

arth_i = 1/2*log((1+x)/(1-x));

endfunction

//== function arcth ====

//function [arcthZ] = arcth(Z,N)

Q0 = 0;

x0 = 1;

Z=2.25;

y0 = Z;

N=40;

Q(1)=Q0+arth(2^(-1));

r(1)=sign(1-y0);

x(1)=x0-r(1)*y0*2^(-1);

y(1)=y0-r(1)*x0*2^(-1);

for n=1:N

for k=2:n

i=1+int((k-1)/2);

r(k)=sign(1-y(k-1));

ARTH =arth(2^(-i));

Q(k)= Q(k-1)+r(k)*ARTH;

x(k)= x(k-1)-r(k)*y(k-1)*2^(-i);

y(k)= y(k-1)-r(k)*x(k-1)*2^(-i);

end

arthZ(n)= Q(n)

y_ist = 1/2*log((1+Z)/(1-Z))

// z_i = (exp(y_ist)+exp(-y_ist))/2

pogr(n)=(y_ist-arthZ(n))/y_ist*100;

end

scf(1);

clf();

plot(pogr);

xgrid();

//endfunction

for n=1:20

m=3;

Q(1)=Q0+arth(2^(-1));

Q(1)=conv(n,m,Q(1));

r(1)=sign(Z-x0);

x(1)=x0+r(1)*y0*2^(-1);

x(1)=conv(n,m,x(1));

y(1)=y0+r(1)*x0*2^(-1);

y(1)=conv(n,m,y(1));

last=26;

for k=2:last

i=1+int((k-1)/2);

r(k)=sign(Z-x(k-1));

ARTH =arth(2^(-i));

ARTH=conv(n,m,ARTH);

Q(k)= Q(k-1)+r(k)*ARTH;

Q(k)=conv(n,m,Q(k));

x(k)= x(k-1)+r(k)*y(k-1)*2^(-i);

x(k)=conv(n,m,x(k));

y(k)= y(k-1)+r(k)*x(k-1)*2^(-i);

y(k)=conv(n,m,y(k));

end

archZ(n)= Q(last);

y_ist = log(Z+sqrt(Z^2-1));

pogr(n)=(y_ist-archZ(n))/y_ist*100;

end

scf(2);

clf();

plot(pogr);

xgrid();

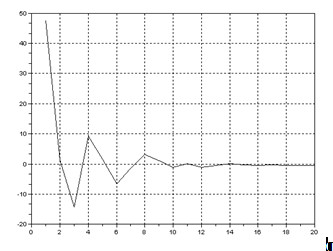
Рис.1.3 - График абсолютной погрешности для функции arcthZ при изменяющемся числе итераций

Рис.1.4 - График абсолютной погрешности для функции arcthZ при изменении разрядности дробной части

Из приведенных графиков видно, что минимальное число итерации должно составить 12, а минимальное число разрядов – 12. То есть рассчитанное число итераций и разрядность данных соответствуют результатам моделирования.