Практичність вивчення кубічних В-сплайнів у вищих навчальних закладах

2.5 Практичність вивчення кубічних В-сплайнів у вищих навчальних закладах

В-сплайни є більш практичні у використанні ніж природні сплайни, оскільки поліноміальні коефіцієнти природних сплайнів вимагають всіх  вузлових точок. Їх обчислення залучає розв’язання  вимірних матриць. У цьому є два недоліки: переміщення однієї вузлової точки зачіпає всю криву і під час розв’язування матриці можна зіткнутися з швидкою зміною кривої. З іншого боку, В-сплайни складаються з сегментів кривих, залежних тільки від кількох вузлових точок. Це називається локальним контролем. Таким чином, переміщення вузлової точки зачіпає тільки маленьку частину кривої. B-сплайни мають ту ж саму неперервність, як і природні сплайни, але не інтерполюють їх вузлові точки. Тому, ми говоримо про наближення багатокутника, а не про вставку вузлової точки.

Першим кроком є вибір порядку базису сплайнів, щоб досягати бажану гладкість і полегшити обчислювання.

Як найефективніші, були вибрані кубічні В-сплайни, тобто сплайни третього порядку, через наступні причини:

1. Поліноми нижніх степенів дають дуже низьку гнучкість в управлінні формою кривої. В-сплайни першого порядку (прямі лінії) не дають задовільної гладкості апроксимуючої кривої. В-сплайни другого порядку дають гладку криву, але проблема виникає в точках, де з'єднуються сегменти кривої. Щоб зрозуміти цю проблему, ми введемо нове означення:

Означення. Позначимо  сегмент кривої. Якщо напрям і величина  і  рівні в точці з'єднання, крива, що складається з цих двох сегментів, називається  неперервною.

В-сплайни другого порядку  і  неперервні, що не гарантує задовільну неперервність в об'єднаних точках. Проблема вирішується, використовуючи кубічні В-сплайни, які є ,  і  і неперервними.

2.Поліноми вищого степеня віднімають багато часу в обчислювальному процесі і можуть нести небажані скачки. Крива може "скакати" назад і вперед важко керованими способами.

3. Кажучи, що кубічні В-сплайни дають "задовільну" неперервність, мається на увазі, що око не може виявити геометричну неоднорідність степеня вище, ніж два і практично досить використовувати В-сплайни третього ступеня [9].

Отже, хоч кубічні В-сплайни і є методом, важчим у розрахунках, ніж інші, відомі методи, які застосовуються у задачах для наближення, але він дає набагато точніший результат, і є просто незамінним при розв’язуванні задач, які неможливо розв’язати іншими методами.

3. Практична частина

3.1 Задача №1

 

Потрібно інтерполювати (використовуючи задачу першого або другого роду) одну з відомих функцій, з допомогою кубічних В-сплайнів, у випадку рівномірної сітки розбиття.

Розв’язання: Для розв’язання цієї задачі візьмемо функцію  і будемо її інтерполювати на відрізку , розбивши його на 6 рівних частин (). Маємо рівномірну сітку, отже будемо користуватися формулою (15’). Знайдемо  і  (задача інтерполяції першого роду): ,

(15’’) Виключимо із системи (16)  і :  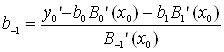, , 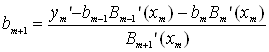(32)

і отримаємо наступну систему:

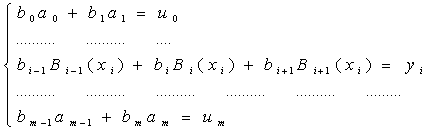
, (33) де

, ,

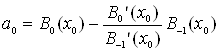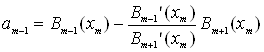, ,(34)

, .

Розв’язавши систему (33), знайдемо коефіцієнти , для шуканого сплайна:

(де у нашому випадку ).

Отже необхідно знайти і підставити відповідні значення та розв’язати матричне рівняння:

,

де  - тридіагональна матриця, а  - шуканий вектор коефіцієнтів.

Для нашої функції  маємо наступні дані:

,,

,,

,,

,,

,,

,,

,,

,.

 

Тоді три діагональна матриця  і вектор  відповідно дорівнюватимуть:

, ,

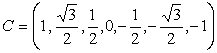підставивши їх у матричне рівняння, отримаємо вектор :

 ,

,.

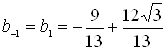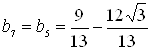Отже, маємо інтерполяційний сплайн функції  на проміжку :

Побудуємо його графік (в середовищі Matlab):

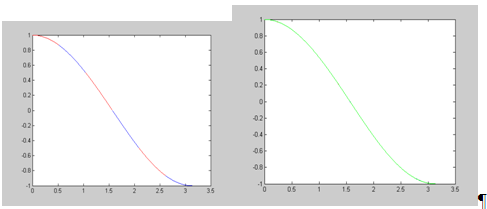
Мал. 4, 5 – Графіки функції

На малюнку 4 зображено графік функції , а на малюнку 5 – графік функції (зображено зеленим кольором), яка накладається на графік функції . Як бачимо наш інтерполяційний сплайн фактично повністю співпадає з і лише при великому збільшенні можна побачити розбіжності (малюнок 6 і 7), тобто має місце незначна похибка. Знайдемо її.

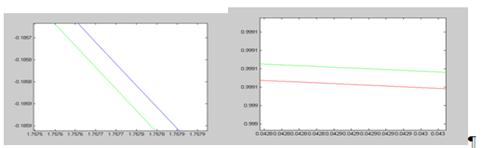
Мал. 6, 7 – Розбіжності

Для цього будемо шукати максимальну похибку на кожному з відрізків розбиття. Скористаємося наступними формулами:

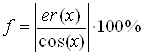,(35)

Отже на проміжку  маємо графік зображений на малюнку 8 (побудований в середовищі Mathcad). Неозброєним оком похибки не видно, але вона є, і це показано на малюнку 9, який зображає функцію .

Мал. 8 – Графік, побудований в середовищі Mathcad

Мал. 9 – Найбільша похибка відрізку

Як видно з малюнка 9, найбільша похибка на даному відрізку приблизно дорівнює:

 при  і відповідно .

Аналогічно розглянемо всі проміжки розбиття і знайдемо максимальні значення похибок на кожному з них, які представлені в наступній таблиці:

сегмент
	0,27	-2,023	0,021%
	0,82	-1,472	0,022%
	1,36	-0,584	0,028%
	1,78	0,584	0,028%
	2,34	1,489	0,021%
	2,88	2,023	0,021%

З таблиці видно, що максимальна похибка менша за 0,03%, і, оскільки, задовільною вважається похибка менша чим 5%, то отриману можна вважати практично нульовою.