Навигация
Базис у просторі кубічних сплайнів
2.2 Базис у просторі кубічних сплайнів
Функція ![]() :
:
а) двічі неперервно диференційовна на відрізку ![]() ;
;
б)відмінна від нуля тільки на чотирьох відрізках ![]()
Відрізок ![]() називають носієм функції
називають носієм функції ![]() [6].
[6].
Доповнимо розбиття ![]() допоміжними вузлами:
допоміжними вузлами:
![]()
![]()
![]() ,взятими довільно.
,взятими довільно.
За розширеною сіткою:
![]() :
:![]()
![]() можна побудувати сім’ю з
можна побудувати сім’ю з ![]() кубічних В-сплайнів:
кубічних В-сплайнів:
![]() ,
, ![]()
Ця сім’я утворює базис в просторі кубічних сплайнів на відрізку ![]() . Тим самим довільний кубічний сплайн
. Тим самим довільний кубічний сплайн ![]() , побудований по розбиттю
, побудований по розбиттю ![]() із
із ![]() вузла, може бути представлений на цьому відрізку в вигляді лінійної комбінації:
вузла, може бути представлений на цьому відрізку в вигляді лінійної комбінації:
![]()
Умовами задачі коефіцієнти ![]() цього розбиття визначаються однозначно [7].
цього розбиття визначаються однозначно [7].
2.3 Задачі інтерполяції з граничними умовами першого та другого роду
У випадку коли задані значення ![]() функції в вузлах сітки і значення
функції в вузлах сітки і значення![]() і
і ![]() першої похідної функції на кінцях сітки (задача інтерполяції з граничними умовами першого роду), коефіцієнти
першої похідної функції на кінцях сітки (задача інтерполяції з граничними умовами першого роду), коефіцієнти ![]() обчислюються із системи наступного вигляду:
обчислюються із системи наступного вигляду:
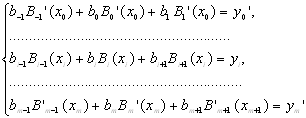 , де
, де ![]() (16)
(16)
Після виключення ![]() і
і ![]() отримується лінійна система з невідомими
отримується лінійна система з невідомими ![]() і 3-діагональною матрицею, яку можна розв’язати, як методом Гауса, так і методом прогонки [8].
і 3-діагональною матрицею, яку можна розв’язати, як методом Гауса, так і методом прогонки [8].
При розв’язанні задачі інтерполяції другого роду використовують значення похідних другого порядку на кінцях сітки: ![]() і
і ![]() . І коефіцієнти
. І коефіцієнти ![]() вже обчислюються із системи:
вже обчислюються із системи:

![]() (16’)
(16’)
таким самим чином, як і під час розв’язування задачі інтерполяції першого роду.
2.4 Апроксимація кубічними В-сплайнами
Нехай задана таблиця чисел ![]() і
і ![]() , котрі є значеннями функції
, котрі є значеннями функції ![]() і її першої похідної
і її першої похідної ![]() у вузлах ai, i =0,1, ..., N. Необхідна апроксимувати функцію W(a) з допомогою цих даних.
у вузлах ai, i =0,1, ..., N. Необхідна апроксимувати функцію W(a) з допомогою цих даних.
Розглянемо апроксимацію кубічними В-сплайнами. Конструкція нормованого

кубічного В-сплайна зазвичай задається так:
 (17)
(17)
В правій частині (17) стоять многочлени третього степеня виду:
![]()
![]() (18)
(18)
Коефіцієнти ai , bi , ci , di визначаються із системи чотирьох рівнянь, отриманих при умовах: ![]()
![]()
![]() и
и ![]() . В результаті її розв’язку можна записати:
. В результаті її розв’язку можна записати:
![]()
![]() (19)
(19)
![]() ,
, ![]() ,
, ![]()
При конкретизації виразу (18) використовуються формули (19), що задовольняють умови стику у вузлах ai-2, ai-1, ai , ai+1 для сплайнів:
 (20)
(20)
Та їх похідних по a, позначених штрихом:
 (21)
(21)
В роботі Б.Зав’ялова [6] для рівномірної сітки ![]() i=0,1, ... , N, задовольняючи наступні умови (20), (21), отримано такий вираз для
i=0,1, ... , N, задовольняючи наступні умови (20), (21), отримано такий вираз для ![]()

Тут ![]() ,
, ![]() а також з’ясовано, що S0=2/3, S*=1/6, S**=1/2h.
а також з’ясовано, що S0=2/3, S*=1/6, S**=1/2h.
Загальний інтерполяційний вираз, в якому використовуються нормовані кубічні В-сплайни (22), записуються так:
![]() , (23)
, (23)
де ![]() , а
, а ![]() . Коефіцієнти
. Коефіцієнти ![]() bi+1,bi+2 визначаються із умов, що задовольняють значення функції W(a), відомих в деяких вузлах
bi+1,bi+2 визначаються із умов, що задовольняють значення функції W(a), відомих в деяких вузлах ![]()
![]() . Зазвичай вибирають
. Зазвичай вибирають ![]() ,
, ![]() , а
, а ![]() задовольняють нерівність:
задовольняють нерівність: ![]() .
.
Запишемо (23) в розгорнутому вигляді. Для цього, використавши (22) отримаємо всі вирази для ![]() . Сплайн
. Сплайн ![]() отримаємо із четвертої рівності (22), якщо там формально замінити x на 1+ x . Тоді
отримаємо із четвертої рівності (22), якщо там формально замінити x на 1+ x . Тоді
![]() (24)
(24)
Вираз для ![]() береться безпосередньо із (22)
береться безпосередньо із (22)
![]() (25)
(25)
Сплайн ![]() записується на основі другої рівності (22) шляхом формальної заміни x на x-1
записується на основі другої рівності (22) шляхом формальної заміни x на x-1
![]() (26)
(26)
І, нарешті із першого виразу (22), замінюючи x на x-2, отримаємо:
![]() . (27)
. (27)
Тоді остаточний варіант інтерполяційного виразу, основаного на застосуванні нормованих кубічних В-сплайнів, отримаємо шляхом підстановки виразів (24)-(27) в (23)
 (28)
(28)
![]()
![]()
Вираз (28) дає четвертий порядок апроксимації функції ![]() по кроку h 0( h4 ) . Якщо в формулі (28) виключити коефіцієнти, виразивши їх через значення апроксимуючої функції у вузлах, то отримаємо:
по кроку h 0( h4 ) . Якщо в формулі (28) виключити коефіцієнти, виразивши їх через значення апроксимуючої функції у вузлах, то отримаємо:
![]() , де (29)
, де (29)
 (30)
(30)
Більш високий порядок апроксимації можна отримати за допомогою так званих напружених сплайнів, при цьому інтерполяційний вираз (29) зберігає свій вигляд, а функції, які входять до його складу задаються так:
![]() , (31) де
, (31) де 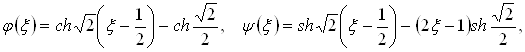
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Інтерполяційний вираз виду (29) використовується, як для визначення шуканих величин між вузлами координатної сітки, так і для апроксимації частинних похідних, котрі входять до складу повної системи рівнянь [8].
0 комментариев