Решается система линейных уравнений (2.1.1)

1. Решается система линейных уравнений (2.1.1).

2. Проверяется выполнение условия (2.1.24).

3. Определяется  по формуле (2.1.26) и проверяется сходимость ряда (2.1.25).

4. Определяются  с помощью соотношения

где

(Формулы (2.1.28), (2.1.29) получаются из (2.1.18), (2.1.19) с учетом персонификации -го узла и того, что на него в изоляции направляется простейший поток с параметром ).

5. Находится стационарное распределение состояний сети  с помощью формулы (2.1.2).

При этом нормировку вероятностей можно производить не  раз, как это делалось в пункте 4, а один раз, исходя из условия . Отметим также, что если в сети есть терминальные узлы, в которых условие (2.1.24) не выполняется, то алгоритм существенно усложнится, так как в этих узлах нельзя применить (2.1.28), (2.1.29). Поэтому для таких узлов необходимо добавить процедуру численного решения системы уравнений (2.1.3) – (2.1.8) с последующей его нормировкой.

Замечание 2.3. Нетрудно понять, что совместное стационарное распределение чисел заявок в узлах имеет следующую форму:

где

а совместное стационарное распределение режимов работы узлов – форму:

где

Исходя из этих соотношений можно построить также алгоритм подсчета числовых характеристик узлов в стационарном режиме. Например, можно найти среднее стационарное число заявок в каждом узле, средний стационарный режим работы каждого узла и т.п. В принципе можно построить алгоритм нахождения совместной стационарной производящей функции чисел заявок и режимов работы в узлах сети, алгоритмы нахождения совместной производящей функции чисел заявок и нахождения совместной производящей функции режимов работы узлов в установившемся состоянии.

Пусть  – часть выходящего из -го узла потока заявок, покидающих сеть  – подмножество нетерминальных узлов . Из леммы 2.2 и результатов работы  вытекает

Следствие 1.1 [43, C.133]. Потоки  являются независимыми пуассоновскими потоками с параметрами  соответственно.

Заметим, что если условию (2.1.23) подчиняются все узлы, то  – независимые пуассоновские потоки.

2 Сети с переключением режимов при определенном количестве заявок в узле

Пусть , где  – вектор, все координаты которого равны нулю кроме  – вектор, все координаты которого равны нулю кроме . На фазовом пространстве  задан многомерный марковский процесс , где , своими инфинитезимальными интенсивностями перехода

Интенсивности перехода из состояния  во все состояния, отличные от вышеперечисленных, предполагаются равными нулю. Здесь , если  и , если  и  и .

Марковский процесс  описывает открытую сеть с простейшим входным потоком с параметром  и вероятностью  направления поступающей заявки в -й узел. В -м узле находится единственный экспоненциальный прибор с интенсивностью обслуживания , зависящей от состояния узла. Заявка, обслуженная в -м узле, переходит с вероятностью  в -й узел, а с вероятностью  покидает сеть. Компонента  выражает число заявок в -м узле, а компонента  – номер режима работы прибора. Прибор -го узла может работать в  режимах  с показательно распределенным временем пребывания в них;  – интенсивность увеличения номера режима на единицу,  – интенсивность уменьшения номера режима на единицу.

Глобальные уравнения равновесия для стационарных вероятностей этого марковского процесса имеют следующую форму:

В 2.1 исследовался случай  при  при . Однако на практике возможна ситуация, когда при определенных числах заявок в узлах режимы могут меняться, а при других числах – нет. Поэтому рассмотрим более общий случай, когда для каждого узла  существует конечное или счетное множество индексов  такое, что  для всех , у которых  для некоторого  и  для всех  иного вида (фактически в 2.1 рассматривался случай ).

Пусть  – положительное решение уравнения трафика

Рассмотрим марковский процесс  на фазовом пространстве , заданный инфинитезимальными интенсивностями

для всех иных состояний  считаем, что . Процесс  описывает изолированный узел в фиктивной окружающей среде, в которой на узел посылается стационарный пуассоновский поток с параметром , где  найдено из уравнения трафика (2.2.1). Уравнения равновесия для стационарных вероятностей марковского процесса, описывающего такой узел, имеют следующий вид:

для

для

для

Мы свяжем стационарное распределение  процесса  со стационарными распределениями  процессов  и будем интересоваться необходимыми и достаточными условиями выполнения равенства

 

Лемма 2.3. Если для рассматриваемой системы входящий поток является простейшим, то обратимость и квазиобратимость эквивалентны.

Д о к а з а т.е. л ь с т в о. Для изолированного узла условие квазиобратимости (2.1.9) принимает вид

а условие обратимости (2.1.10) – форму

и для

Достаточно показать, что при выполнении (2.2.2) – (2.2.7) из (2.2.9) следует (2.2.10). Пусть  при некотором фиксированном . Докажем, что тогда для всех  выполняется (2.2.10). При  соотношение (2.2.10) следует из (2.2.4) и соотношения (2.2.9) для состояний  и . Предположим, что (2.2.10) выполняется для некоторого , т.е.

Тогда из (2.2.5) с учетом (2.2.11) и (2.2.9) для состояний  и  вытекает (2.2.10). Итак, (2.2.10) доказано с помощью индукции по . Лемма доказана.

Лемма 2.4 [45, C.184]. Для квазиобратимости изолированного -го узла необходимо и достаточно выполнения условий

а) для  при некотором

б) для всех

 

При выполнении (2.2.12) для эргодичности  достаточно, чтобы сходился ряд

 

где . Финальное стационарное распределение процесса  определяется соотношениями

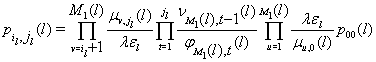
где предполагается, что произведение, в котором нижний индекс больше верхнего, равно единице, а

Д о к а з а т.е. л ь с т в о. Рассмотрим случайное блуждание по точкам с целочисленными координатами первого квадранта плоскости, задаваемое уравнениями (2.2.2) – (2.2.7). Как уже ранее говорилось, для обратимости стационарного марковского процесса необходимо и достаточно, чтобы выполнялось циклическое условие Колмогорова: для любых различных состояний

Более того, известно, что для обратимости достаточно, чтобы условие (2.2.18) выполнялось для любых замкнутых путей из  в  без самопересечений. Равенство (2.2.12) есть условие Колмогорова (2.2.18) для четырехзвенных путей, проходящих через вершины элементарного квадрата  и идущих из  в  по и против часовой стрелки. Равенство (2.2.13) есть условие Колмогорова для -звенных путей, проходящих через вершины прямоугольника  и ведущих из  в  по и против часовой стрелки. Это доказывает необходимость условий (2.2.12) и (2.2.13) для обратимости, а значит (по лемме 2.3) квазиобратимости изолированного узла в фиктивной окружающей среде. Предположим, что (2.2.12), (2.2.13) выполнены. Любой замкнутый путь из  в  без самопересечений либо а) представляет собой некоторую однозвенную замкнутую дугу, либо б) проходит по границе некоторой фигуры, составленной из конечного числа примыкающих друг к другу элементарных квадратов и определенных выше - звенных прямоугольников. Для случая а) циклическое условие (2.2.18) выполняется автоматически. В случае б) перемножим равенства (2.2.12) для всех элементарных квадратов и равенства (2.2.13) для всех прямоугольников, из которых состоит упомянутая фигура. Так как прямоугольники могут соприкасаться только «длинными» сторонами, то при этом интенсивности перехода для тех направленных дуг, которые не принадлежат границе фигуры, войдут множителями как в левую, так и в правую части. После сокращения на них получится циклическое условие (2.2.18) для путей, идущих по границе фигуры по и против часовой стрелки. Достаточность условий (2.2.12) и (2.2.13) доказана.

Отметим также, что в силу того, что примененные в доказательстве элементарные квадраты и прямоугольники имеют в качестве замкнутых путей, идущих по их границам минимальные циклы, т.е. замкнутые пути с минимальным числом вершин, то условия (2.2.12) и (2.2.13) нельзя, вообще говоря, ослабить, и они являются минимально достаточными.

Докажем, что стационарное распределение изолированного узла в фиктивной окружающей среде имеет форму (2.2.15), (2.2.16). Полагая в (2.2.10)  получим:

откуда получаем

Из (2.2.9) для  находим, что

Для таких же  из (2.2.9) также следует, что

в частности,

Подставляя (2.2.21) в (2.2.19), а затем подставляя полученное равенство в (2.2.20), будем иметь для

Тем самым доказано (2.2.15).

Для  из (2.2.9) следует, что

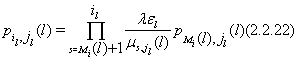
Полагая в (2.2.10) , получим:

откуда

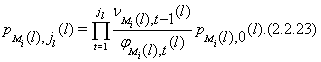
Далее, из (2.2.9)

Подставляя (2.2.24) в (2.2.23), а затем полученное равенство в (2.2.22), для  будем иметь

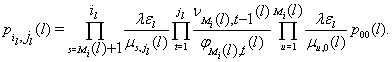
Таким образом, (2.2.16) доказано.

Наконец, (2.2.17) следует из того, что сумма всех стационарных вероятностей равна единице:

Достаточность сходимости ряда (2.2.14) для эргодичности  вытекает из теоремы Фостера . Лемма 2.4 доказана полностью.

Основной результат 2.2 заключается в следующем.

Теорема 2.2. [45, C.184] Для выполнения (2.2.8) необходимо и достаточно, чтобы в нетерминальных узлах выполнялись условия (2.2.12), (2.2.13). При выполнении этого условия для эргодичности марковского процесса , описывающего поведение сети, достаточно, чтобы сходился ряд

где

При этом в нетерминальных узлах стационарное распределение процесса  имеет форму (2.2.15) – (2.2.17).

Д о к а з а т.е. л ь с т в о. В  для открытых сетей с «заявкосохраняющими» узлами установлено, что для мультипликативности стационарного распределения необходимо и достаточно, чтобы нетерминальные узлы являлись квазиобратимыми. Поэтому, с учетом условия квазиобратимости (2.1.16) для изолированного узла, которое в силу леммы 2.4 для узла с номером  принимает форму (2.2.12), (2.2.13) имеет место первое утверждение теоремы.

Докажем, что при выполнении условия (2.2.25) процесс  эргодичен. Как отмечалось ранее,  неприводим. Остается воспользоваться эргодической теоремой Фостера , согласно которой достаточно проверить, что система уравнений

где  – интенсивность перехода  из состояния  в состояние ; , определяемая посредством (2.2.26), – интенсивность выхода  из состояния , имеет нетривиальное решение  такое, что . Действительно, беря , где  определяется (2.2.8), получим, что (2.2.27) превращаются в глобальные уравнения равновесия для сети, которым  удовлетворяет. А ряд  сходится, так как его члены отличаются от членов ряда (2.2.25) постоянным множителем.

Замечание 2.3. Отметим, что для эргодичности марковского процесса  достаточно потребовать выполнения следующих двух условий, гарантирующих сходимость ряда (2.2.25):

для всех

1) сходятся ряды

Здесь условие 2) гарантирует регулярность марковского процесса, который не может за конечное время делать бесконечное число скачков из одного состояния в другое.

Замечание 2.4. Если условия (2.2.12), (2.2.13) выполнены во всех узлах и ряд (2.2.25) сходится, то получается простой алгоритм для нахождения стационарных вероятностей: