Навигация
1. Основная модель
Рассматриваются открытые сети массового обслуживания с простейшим входящим потоком, экспоненциальным обслуживанием в узлах и марковской маршрутизацией. Однолинейные узлы могут работать в нескольких режимах, время переключения с одного режима на другой имеет показательное распределение. Переключение происходит только на соседние режимы. Устанавливается условие квазиобратимости узлов, условие эргодичности сети и для квазиобратимого случая находится стационарное распределение состояний сети в мультипликативной форме.
Постановка задачи
В подавляющем числе работ, посвященных сетям массового обслуживания с мультипликативной формой стационарного распределения, используется понятие квазиобратимости. Это вызвано тем, что квазиобратимость узлов гарантирует существование инвариантной меры в форме произведения для соответствующего сети марковского процесса. Здесь нами также используется понятие квазиобратимости.
Аналитические модели сетей с ненадежными приборами почти не рассматривались в литературе в силу сложности нахождения инвариантной меры. Наша постановка позволяет исследовать сети, в которых приборы могут частично выходить из строя, работая при этом в «щадящем» режиме.
В сеть, состоящую из ![]() однолинейных узлов, поступает стационарный пуассоновский поток заявок с параметром
однолинейных узлов, поступает стационарный пуассоновский поток заявок с параметром ![]() . Каждая заявка входного потока независимо от других заявок с вероятностью
. Каждая заявка входного потока независимо от других заявок с вероятностью ![]() направляется в
направляется в ![]() -й узел
-й узел ![]() .Заявка, обслуженная в
.Заявка, обслуженная в ![]() -м узле, мгновенно с вероятностью
-м узле, мгновенно с вероятностью ![]() направляется в
направляется в ![]() -й узел, а с вероятностью
-й узел, а с вероятностью ![]() покидает сеть
покидает сеть ![]() В
В ![]() -м узле находится единственный прибор, который может работать в
-м узле находится единственный прибор, который может работать в ![]() режимах. Состояние
режимах. Состояние ![]() -го узла характеризуется парой чисел
-го узла характеризуется парой чисел ![]() , где
, где ![]() – число заявок в
– число заявок в ![]() -м узле,
-м узле, ![]() – номер режима, в котором работает прибор в
– номер режима, в котором работает прибор в ![]() -м узле
-м узле ![]() . Длительность обслуживания прибором
. Длительность обслуживания прибором ![]() -го узла, находящегося в состоянии
-го узла, находящегося в состоянии ![]() , имеет показательное распределение с параметром
, имеет показательное распределение с параметром ![]() , зависящим от состояния (т.е. от числа заявок
, зависящим от состояния (т.е. от числа заявок ![]() в узле и режима
в узле и режима ![]() его работы). Назовем 0 основным режимом работы. Время пребывания в основном режиме работы имеет показательное распределение с параметром
его работы). Назовем 0 основным режимом работы. Время пребывания в основном режиме работы имеет показательное распределение с параметром ![]() , после чего прибор переходит в режим 1. Для состояний
, после чего прибор переходит в режим 1. Для состояний ![]() , у которых
, у которых ![]() , время пребывания в режиме
, время пребывания в режиме ![]() также имеет показательное распределение, при этом с интенсивностью
также имеет показательное распределение, при этом с интенсивностью ![]() прибор
прибор ![]() -го узла переходит в режим
-го узла переходит в режим ![]() , а с интенсивностью
, а с интенсивностью ![]() – в режим
– в режим ![]() . Время пребывания в последнем
. Время пребывания в последнем ![]() -м режиме имеет показательное распределение с параметром
-м режиме имеет показательное распределение с параметром ![]() , после чего прибор переходит в
, после чего прибор переходит в ![]() -й режим. Во время переключения прибора с одного режима работы на другой число заявок в узле не меняется.
-й режим. Во время переключения прибора с одного режима работы на другой число заявок в узле не меняется.
Переход с режима 0 в режим 1 можно трактовать как частичную потерю работоспособности прибора, влекущую уменьшение интенсивности обслуживания с величины ![]() на
на ![]() . Аналогично, переход с режима
. Аналогично, переход с режима ![]() в режим
в режим ![]() означает переход прибора в более щадящий режим обслуживания. Переход с режима
означает переход прибора в более щадящий режим обслуживания. Переход с режима ![]() в режим
в режим ![]() означает восстановление тех функциональных возможностей, которые были утеряны прибором при переходе с режима
означает восстановление тех функциональных возможностей, которые были утеряны прибором при переходе с режима ![]() в режим
в режим ![]() .
.
Состояние сети в момент времени ![]() будем характеризовать вектором
будем характеризовать вектором ![]() , где
, где ![]() – состояние
– состояние ![]() -го узла в момент времени
-го узла в момент времени ![]() . В соответствии с вышесказанным здесь
. В соответствии с вышесказанным здесь ![]() – число заявок в
– число заявок в ![]() -м узле в момент
-м узле в момент ![]() ,
, ![]() – номер режима работы
– номер режима работы ![]() -го узла в момент
-го узла в момент ![]() .
.
Предположим, что ![]() , если
, если ![]() и
и ![]() , если
, если ![]() , если
, если ![]() и
и ![]() , если
, если ![]() , если
, если ![]() и
и ![]() , если
, если ![]() , а уравнение трафика
, а уравнение трафика
![]()
имеет единственное решение ![]() для которого
для которого ![]() (для этого достаточно, чтобы матрица
(для этого достаточно, чтобы матрица ![]() , где
, где ![]() , была неприводимой). Тогда
, была неприводимой). Тогда ![]() – неприводимый марковский процесс на фазовом пространстве
– неприводимый марковский процесс на фазовом пространстве ![]() , где
, где ![]() .
.
Цель 2.1 состоит в установлении условий эргодичности ![]() и выяснении необходимых и достаточных условий, при которых стационарное финальное распределение процесса
и выяснении необходимых и достаточных условий, при которых стационарное финальное распределение процесса ![]() , где
, где ![]() , представляется в мультипликативной форме
, представляется в мультипликативной форме
![]()
где ![]() зависит только от состояния
зависит только от состояния ![]() -го узла.
-го узла.
Отметим, что интенсивности перехода ![]() процесса
процесса ![]() из состояния
из состояния ![]() в состояние
в состояние ![]() равны
равны
![]()
![]()
![]()
для всех иных состояний ![]() они равны нулю. Здесь
они равны нулю. Здесь ![]() – вектор, все координаты которого равны нулю кроме
– вектор, все координаты которого равны нулю кроме ![]() – вектор, все координаты которого равны нулю кроме
– вектор, все координаты которого равны нулю кроме ![]() – индикатор множества
– индикатор множества ![]() .
.
Анализ изолированного узла
Для упрощения обозначений в данном разделе будет опускаться индекс ![]() , указывающий номер узла. Например,
, указывающий номер узла. Например, ![]() – состояние узла,
– состояние узла, ![]() – пространство состояний узла,
– пространство состояний узла, ![]() – номер режима работы прибора в узле,
– номер режима работы прибора в узле, ![]() – стационарное распределение состояний узла и т.д. Рассмотрим изолированный узел, и предположим, что на него поступает простейший поток заявок с интенсивностью
– стационарное распределение состояний узла и т.д. Рассмотрим изолированный узел, и предположим, что на него поступает простейший поток заявок с интенсивностью ![]() . Если стационарное распределение существует, то стационарные вероятности удовлетворяют следующей системе уравнений равновесия:
. Если стационарное распределение существует, то стационарные вероятности удовлетворяют следующей системе уравнений равновесия:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Для «заявко-сохраняющих» систем массового обслуживания (т.е. для которых совпадают средние интенсивности поступления и ухода заявок) один из возможных способов определения квазиобратимости выглядит следующим образом. Если на вход системы направлять простейший поток заявок с параметром ![]() , то система называется квазиобратимой, если
, то система называется квазиобратимой, если
![]()
Здесь ![]() – часть интенсивности перехода системы из состояния
– часть интенсивности перехода системы из состояния ![]() в состояние
в состояние ![]() , обусловленная обслуживанием заявок. Напомним, что система называется обратимой, если для любых ее состояний
, обусловленная обслуживанием заявок. Напомним, что система называется обратимой, если для любых ее состояний ![]() и
и ![]()
![]()
где ![]() – интенсивность перехода системы из состояния
– интенсивность перехода системы из состояния ![]() в состояние
в состояние ![]() . Известно, что для систем с простейшим входящим потоком обратимость влечет квазиобратимость. Обратное утверждение, вообще говоря, неверно.
. Известно, что для систем с простейшим входящим потоком обратимость влечет квазиобратимость. Обратное утверждение, вообще говоря, неверно.
Для рассматриваемой нами задачи условие квазиобратимости (2.1.9) принимает вид
![]()
а условие обратимости (2.1.10) – форму
![]()
![]()
Лемма 1.1 [43, C.131]. Если для рассматриваемой системы входящий поток является простейшим, то обратимость и квазиобратимость эквивалентны.
Д о к а з а т.е. л ь с т в о. Достаточно показать, что при выполнении (2.1.3) – (2.1.8) из (2.1.11) следует (2.1.12). Сначала докажем, что для всех ![]() выполняется (2.1.12) при
выполняется (2.1.12) при![]() , т.е. равенство
, т.е. равенство
![]()
При ![]() соотношение (2.1.13) следует из (2.1.3) и соотношения (2.1.11), в котором
соотношение (2.1.13) следует из (2.1.3) и соотношения (2.1.11), в котором ![]() . Предположим, что (2.1.13) выполняется для некоторого
. Предположим, что (2.1.13) выполняется для некоторого ![]() , т.е.
, т.е.
![]()
Тогда из (2.1.4) с учетом (2.1.14) и (2.1.11) при ![]() следует (2.1.9). Итак, (2.1.9) доказано с помощью индукции по
следует (2.1.9). Итак, (2.1.9) доказано с помощью индукции по ![]() .
.
Теперь докажем, что для всех ![]() выполняется (2.1.12) при
выполняется (2.1.12) при ![]() . При
. При ![]() соотношение (2.1.12) следует из (2.1.6) и (2.1.11). Предположим, что (2.1.12) верно для некоторого
соотношение (2.1.12) следует из (2.1.6) и (2.1.11). Предположим, что (2.1.12) верно для некоторого ![]() , т.е.
, т.е.
![]()
Тогда (2.1.12) вытекает из (2.1.7), (2.1.11) и (2.1.15). Лемма доказана.
Лемма 1.2 [43, C.131]. Для квазиобратимости изолированного узла необходимо и достаточно выполнения условий
![]()
При выполнении (2.1.16) для эргодичности ![]() достаточно, чтобы
достаточно, чтобы
![]()
Финальное стационарное распределение процесса ![]() определяется соотношениями
определяется соотношениями
![]()
где предполагается, что произведение, в котором нижний индекс больше верхнего, равно единице, а

Д о к а з а т.е. л ь с т в о. Рассмотрим случайное блуждание по точкам с целочисленными координатами первого квадранта плоскости с возможными переходами в соседние (слева, справа, сверху, снизу) состояния и обычной модификацией для точек на координатных осях. Покажем, что для его обратимости необходимо и достаточно, чтобы для всех ![]()
![]()
![]()
что выражает равенство произведения интенсивностей перехода по замкнутому пути, проходящему через вершины элементарного квадрата ![]() и ведущему из вершины
и ведущему из вершины ![]() в себя по часовой стрелке, такому же произведению интенсивностей по пути против часовой стрелки. Известно
в себя по часовой стрелке, такому же произведению интенсивностей по пути против часовой стрелки. Известно ![]() , что для обратимости стационарного марковского процесса необходимо и достаточно, чтобы выполнялось циклическое условие Колмогорова: для любых различных состояний
, что для обратимости стационарного марковского процесса необходимо и достаточно, чтобы выполнялось циклическое условие Колмогорова: для любых различных состояний ![]()
![]()
Более того, известно, что для обратимости достаточно, чтобы условие (2.1.21) выполнялось для любых замкнутых путей из ![]() в
в ![]() без самопересечений. Равенство (2.1.20) есть условие Колмогорова (2.1.21) для четырехзвенных путей, проходящих через вершины элементарного квадрата. Это доказывает необходимость условия (2.1.20). Предположим, что (2.1.20) выполнено. Любой замкнутый путь из
без самопересечений. Равенство (2.1.20) есть условие Колмогорова (2.1.21) для четырехзвенных путей, проходящих через вершины элементарного квадрата. Это доказывает необходимость условия (2.1.20). Предположим, что (2.1.20) выполнено. Любой замкнутый путь из ![]() в
в ![]() без самопересечений либо а) представляет собой некоторую однозвенную замкнутую дугу, либо б) проходит по границе некоторой фигуры, составленной из конечного числа примыкающих друг к другу элементарных квадратов. Для случая а) циклическое условие (2.1.21) выполняется автоматически. В случае б) перемножим равенства (2.1.20) для всех элементарных квадратов, из которых состоит упомянутая фигура. При этом интенсивности перехода для тех направленных дуг, которые не принадлежат границе фигуры, войдут множителями как в левую, так и в правую части. После сокращения на них получится циклическое условие (2.1.21) для путей, идущих по границе фигуры по и против часовой стрелки. Достаточность условия (2.1.20) доказана.
без самопересечений либо а) представляет собой некоторую однозвенную замкнутую дугу, либо б) проходит по границе некоторой фигуры, составленной из конечного числа примыкающих друг к другу элементарных квадратов. Для случая а) циклическое условие (2.1.21) выполняется автоматически. В случае б) перемножим равенства (2.1.20) для всех элементарных квадратов, из которых состоит упомянутая фигура. При этом интенсивности перехода для тех направленных дуг, которые не принадлежат границе фигуры, войдут множителями как в левую, так и в правую части. После сокращения на них получится циклическое условие (2.1.21) для путей, идущих по границе фигуры по и против часовой стрелки. Достаточность условия (2.1.20) доказана.
Для рассматриваемого нами блуждания (2.1.20) превращается в (2.1.16), что доказывает первое утверждение леммы 2.2.
Из (2.1.11) следует, что
![]()
а из (2.1.12) вытекает, что
![]()
Подстановка (2.1.23) в (2.1.22) доказывает (2.1.18). Достаточность сходимости ряда (2.1.17) для эргодичности ![]() вытекает из теоремы Фостера
вытекает из теоремы Фостера ![]() . Лемма 2.2 доказана.
. Лемма 2.2 доказана.
Стационарное распределение сети
Следуя [32,33], ![]() -й узел назовем терминальным или оконечным, если
-й узел назовем терминальным или оконечным, если ![]() . Основной результат формулируется следующим образом.
. Основной результат формулируется следующим образом.
Теорема 1.1 [43, C.132]. Для того, чтобы стационарное распределение открытой сети с многорежимными стратегиями обслуживания в узлах представлялось в форме произведения (2.1.2), необходимо и достаточно, чтобы в нетерминальных узлах выполнялось условие
![]()
При выполнении этого условия для эргодичности марковского процесса ![]() , описывающего поведение сети, достаточно, чтобы сходился ряд
, описывающего поведение сети, достаточно, чтобы сходился ряд
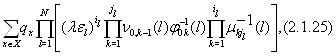
где ![]() – положительное решение уравнения трафика (2.1.1),
– положительное решение уравнения трафика (2.1.1),
![]()
причем для случаев, когда ![]() не определены, они полагаются равными нулю.
не определены, они полагаются равными нулю.
Д о к а з а т.е. л ь с т в о. В ![]() для открытых сетей с «заявкосохраняющими» узлами установлено, что для мультипликативности стационарного распределения необходимо и достаточно, чтобы нетерминальные узлы являлись квазиобратимыми. Поэтому, с учетом условия квазиобратимости (2.1.16) для изолированного узла, которое для узла с номером
для открытых сетей с «заявкосохраняющими» узлами установлено, что для мультипликативности стационарного распределения необходимо и достаточно, чтобы нетерминальные узлы являлись квазиобратимыми. Поэтому, с учетом условия квазиобратимости (2.1.16) для изолированного узла, которое для узла с номером ![]() принимает форму (2.1.24), имеет место первое утверждение теоремы.
принимает форму (2.1.24), имеет место первое утверждение теоремы.
Докажем, что при выполнении условия (2.1.24) процесс ![]() эргодичен. Как отмечалось ранее,
эргодичен. Как отмечалось ранее, ![]() неприводим. Остается воспользоваться эргодической теоремой Фостера
неприводим. Остается воспользоваться эргодической теоремой Фостера ![]() , согласно которой достаточно проверить, что система уравнений
, согласно которой достаточно проверить, что система уравнений
![]()
где ![]() – интенсивность перехода
– интенсивность перехода ![]() из состояния
из состояния ![]() в состояние
в состояние ![]() ;
; ![]() , определяемая посредством (2.1.26), – интенсивность выхода
, определяемая посредством (2.1.26), – интенсивность выхода ![]() из состояния
из состояния ![]() , имеет нетривиальное решение
, имеет нетривиальное решение ![]() такое, что
такое, что ![]() . Действительно, беря
. Действительно, беря ![]() , где
, где ![]() определяется (2.1.2), получим, что (2.1.27) превращаются в глобальные уравнения равновесия для сети, которым
определяется (2.1.2), получим, что (2.1.27) превращаются в глобальные уравнения равновесия для сети, которым ![]() удовлетворяет. А ряд
удовлетворяет. А ряд ![]() сходится, так как его члены отличаются от членов ряда (2.1.25) постоянным множителем.
сходится, так как его члены отличаются от членов ряда (2.1.25) постоянным множителем.
Замечание 2.1. Отметим, что для эргодичности марковского процесса ![]() достаточно потребовать выполнения следующих двух условий, гарантирующих выполнение (2.1.25):
достаточно потребовать выполнения следующих двух условий, гарантирующих выполнение (2.1.25):
1) сходится ряд

![]()
Здесь условие 2) гарантирует регулярность марковского процесса, который не может за конечное время делать бесконечное число скачков из одного состояния в другое.
Замечание 2.2. Если условие (2.1.24) выполнено во всех узлах и ряд (2.1.25) сходится, то получается простой алгоритм для нахождения стационарных вероятностей:
Похожие работы
... из сети провести крайне трудно, так как эти потоки являются сложными благодаря воздействию отрицательных заявок и из-за нелинейности уравнений трафика. 2. ОТКРЫТЫЕ СЕТИ С МНОГОРЕЖИМНЫМИ СТРАТЕГИЯМИ ОБСЛУЖИВАНИЯ И ИНФОРМАЦИОННЫМИ СИГНАЛАМИ ДВУХ ТИПОВ В 1 исследовалось стационарное распределение марковского процесса, описывающего открытую сеть с многорежимными стратегиями обслуживания и ...
... значит, уменьшение интенсивности обслуживания. Поэтому в диссертационной работе предпринята попытка построения моделей, адекватно описывающих такую ситуацию. Рассмотрены экспоненциальные сети с многорежимными стратегиями обслуживания, в которых обслуживающие устройства в узлах частично ненадежны и в различных режимах функционирования работают с разными интенсивностями. Для таких сетей находится ...
0 комментариев