Навигация
Метод Гауса з вибором головного елемента
1.3 Метод Гауса з вибором головного елемента
1. Основна ідея методу. Може трапитись, що система
Ax=f (1)
де A - матриця m*m, x = (x1, x2...,xm) - шуканий вектор
f =(f1, f2..., fm) -заданий вектор.
має єдиний розв’язок, хоча який-небудь з кутового мінору матриці А рівний нулю. В цьому випадку звичайний метод Гауса виявляється непридатним, але може бути застосований метод Гауса з вибором головного елементу.
Основна ідея методу полягає в тому, щоб на черговому кроці виключати не наступне по номеру невідоме, а те невідоме, коефіцієнт при якому є найбільшим по модулю. Таким чином, як провідний елемент тут вибирається головний, тобто найбільший по модулю елемент. Тим самим, якщо ![]() , то в процесі обчислень не відбуватиметься ділення на нуль.
, то в процесі обчислень не відбуватиметься ділення на нуль.
Різні варіанти методу Гауса з вибором головного елементу проілюструємо на прикладі системи з двох рівнянь:
![]() (2)
(2)
![]()
Припустимо, що ![]() . Тоді на першому кроці виключатимемо змінне
. Тоді на першому кроці виключатимемо змінне ![]() . Такий прийом еквівалентний тому, що система (2) переписується у вигляді:
. Такий прийом еквівалентний тому, що система (2) переписується у вигляді:
![]() (3)
(3)
![]()
і до (3) застосовується перший крок звичайного методу Гауса. Вказаний спосіб виключення називається методом Гауса з вибором головного елементу по рядку. Він еквівалентний застосуванню звичайного методу Гауса до системи, в якій на кожному кроці виключення проводиться відповідна перенумерация змінних.
Застосовується також метод Гауса з вибором головного елементу по стовпцю. Припустимо, що ![]() . Перепишемо систему (2) у вигляді:
. Перепишемо систему (2) у вигляді:
![]()
![]()
і до нової системи застосуємо на першому кроці звичайний метод Гауса. Таким чином, метод Гауса з вибором головного елементу по стовпцю еквівалентний застосуванню звичайного методу Гауса до системи, в якій на кожному кроці виключення проводиться відповідна перенумерация рівнянь.
Іноді застосовується і метод Гауса з вибором головного елементу по всій матриці, коли як ведучий вибирається максимальний по модулю елемент серед всіх елементів матриці системи.
2. Матриці перестановок. Раніше було показано, що звичайний метод Гауса можна записати у вигляді:
![]()
![]()
де ![]() -- елементарні нижні трикутні матриці. Щоб отримати аналогічний запис методу Гауса з вибором головного елементу, необхідно розглянути матриці перестановок.
-- елементарні нижні трикутні матриці. Щоб отримати аналогічний запис методу Гауса з вибором головного елементу, необхідно розглянути матриці перестановок.
Означення 1. Матрицею перестановок Р називається квадратна матриця, у якої в кожному рядку і в кожному стовпці тільки один елемент відмінний від нуля і рівний одиниці.
Означення 2. Елементарною матрицею перестановок ![]() називається матриця, отримана з одиничної матриці перестановкою к-го і l-го рядків.
називається матриця, отримана з одиничної матриці перестановкою к-го і l-го рядків.
Наприклад, елементарними матрицями перестановок третього порядку є матриці:
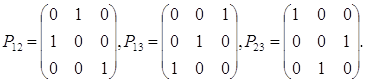
Можна відзначити наступні властивості елементарних матриць перестановок, витікаючі безпосередньо з їх визначення.
1) Добуток двох (а отже, і будь-якого числа) елементарних матриць перестановок є матриця перестановок (не обов'язково елементарною).
2) Для будь-якої квадратної матриці А матриця відрізняється від А перестановкою к-го і l-го стовпців.
3) Для будь-якої квадратної матриці А матриця відрізняється від А перестановкою к-го і l-го стовпців.
Застосування елементарних матриць перестановок для опису методу Гауса з вибором головного елементу по стовпцю можна пояснити на наступному прикладі системи третього порядку:
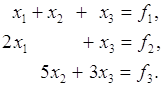 (4)
(4)
Система має вигляд (1), де
 (5)
(5)
Максимальний елемент першого стовпця матриці А знаходиться в другому рядку. Тому треба поміняти місцями другий і перший рядки і перейти до еквівалентної системи
 (6)
(6)
Систему (6) можна записати у вигляді
![]() (7)
(7)
тобто вона виходить з системи (4) шляхом множення на матрицю перестановок
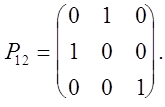
Далі, до системи (6) треба застосувати перший крок звичайного методу виключення Гауса. Цей крок еквівалентний множенню системи (7) на елементарну нижню трикутну

В результаті від системи (7) перейдемо до еквівалентної
![]() (8)
(8)
або в розгорненому вигляді:
 (9)
(9)
З останніх двох рівнянь системи (9) треба тепер виключити змінне ![]() . Оскільки максимальним елементом першого стовпця укороченої системи
. Оскільки максимальним елементом першого стовпця укороченої системи
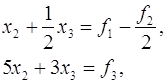 (10)
(10)
є елемент другого рядка, робимо в (10) перестановку рядків і тим самим від системи (9) переходимо до еквівалентної системи, яку можна записати в матричному вигляді як:
![]() . (12)
. (12)
Таким чином система (12) отримана з (8) застосуванням элементарної матриці перестановок:
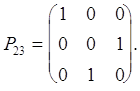
Далі до системи (11) треба застосувати другий крок виключення звичайного методу Гауса. Це еквівалентно множенню системи (11) на елементарну нижню трикутну
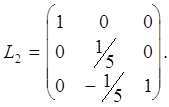
В результаті отримаємо систему
![]() (13)
(13)
або  (14)
(14)
Завершальний крок прямого ходу методу Гауса полягає в заміні останнього рівняння системи (14)
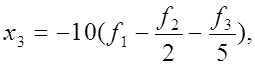
що еквівалентно множенню (13) на елементарну нижню трикутну матрицю

Таким чином, для розглянутого прикладу процес виключення Гауса з вибором головного елементу по стовпцю записується так
![]() (15)
(15)
По побудові матриця
![]() (16)
(16)
є верхньою трикутною матрицею з одиничною головною діагоналлю.
Відмінність від звичайного методу Гауса полягає в тому, що як співмножники в (16) разом з елементарними трикутними матрицями ![]() можуть бути присутніми елементарні матриці перестановок
можуть бути присутніми елементарні матриці перестановок ![]() .
.
Покажемо ще, що з (16) слідує розкладання
PA=LU (17)
L -нижняя трикутна матриця, що має обернену, P - матриця перестановок.
Для цього знайдемо матрицю:
![]() (18)
(18)
Матриця отримується з матриці ![]() перестановкою другого і третього рядків:
перестановкою другого і третього рядків:

Матриця отримується з ![]() перестановкою другого і третього стовпців
перестановкою другого і третього стовпців

тобто ![]() -нижняя трикутна матриця, що має зворотну.т.е.
-нижняя трикутна матриця, що має зворотну.т.е.
З (18), враховуючи рівність![]() , отримаємо
, отримаємо
![]() (19)
(19)
Звідси і з (16) видно, що
![]()
де позначено ![]() . Оскільки Р-матрица перестановок і L-нижняя трикутна матриця, властивість (17) доведена. Воно означає, що метод Гауса з вибором головного елементу по стовпцю еквівалентний звичайному методу Гауса, застосованому до матриці РА, тобто до системи, отриманої з початкової системи перестановкою деяких рівнянь.
. Оскільки Р-матрица перестановок і L-нижняя трикутна матриця, властивість (17) доведена. Воно означає, що метод Гауса з вибором головного елементу по стовпцю еквівалентний звичайному методу Гауса, застосованому до матриці РА, тобто до системи, отриманої з початкової системи перестановкою деяких рівнянь.
Похожие работы
... ’язок де С1, С2 - довільні сталі. Загальний розв’язок системи лінійних алгебраїчних рівнянь подається не в одному й тому самому вигляді. 2. Метод Гауса Метод Гауса розв’язування системи лінійних алгебраїчних рівнянь полягає в послідовному виключенні змінних і перетворенні системи рівнянь (1) до трикутного вигляду (2) Припустимо, що в системі (1) коефіцієнт . Якщо ця ...
... . Істотним недоліком цього методу є неможливість сформулювати умови сумісності і визначеності системи залежно від значень коефіцієнтів і вільних членів. З іншого боку, навіть для визначеної системи цей метод не дає змоги знайти загальні формули, що визначають розв’язки системи через її коефіцієнти і вільні члени, які необхідно мати для теоретичних досліджень. Існують й інші методи розв’язування і ...
... чного сплайну. ; . Для знаходження коефіцієнті вкубічного сплайну призначена програма Work2_2. //------------------------------------------------------------ // Work2_2.cpp //------------------------------------------------------------ // "Числові методи" // Завдання 2 // Інтерполювання функції кубічним сплайном #include <stdio.h> #include <iostream.h> #include <conio ...
... (меньше 0,33%) одного з вільних членів системи (3) зовсім змінило розв’язок системи. На щастя, на практиці системи рівнянь, погано обумовлені, зустрічаються дуже рідко. 1.2 Методи розв’язування задачі Метод Жордана-Гаусса був розроблений двома вченими Жорданом та Гаусом (ві яких і пішла назва методу). Цей метод вони помітили після довгої практики роботи з системами рівнянь. Це можна ...
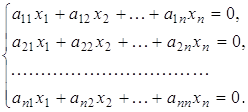
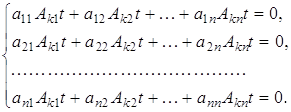
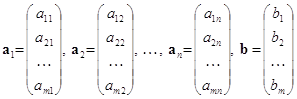

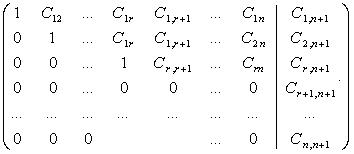
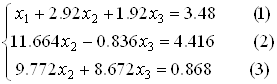
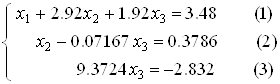
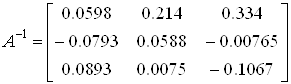
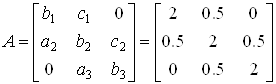
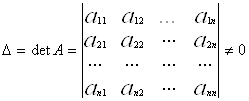
0 комментариев