Навигация
Зміст
Вступ
1. Теоретична частина
1.1 Постановка задачі
1.2 Методи розв'язування задачі
1.3 Алгоритм розв'язку задачі
2. Практична частина
2.1 Архітектура програми
2.2 Опис програми
2.3 Контрольний приклад та результат машинного експерименту
Висновок
Список використаної літератури
Додатки
Вступ
Центральним поняттям програмування є, безперечно, поняття алгоритму. З нього починається робота над програмою і від якості алгоритму залежить її успішне створення. Тому вміння програмувати в значній мірі означає розробляти хороші алгоритми і застосовувати вже відомі.
На сьогодні існує велика кількість різноманітних мов програмування, кожна з яких має свої певні переваги та недоліки. В цьому розмаїтті не завжди легко зробити свій вибір на користь якоїсь певної мови програмування.
Для реалізації поставленої задачі вибрано середовище Turbo Pascal. Алгоритмічна мова Паскаль була створена Н.Віртом на початку 70-х років. Завдяки зусиллям розробників ця мова програмування стала потужним інструментом професійних програмістів‚ не втративши простоти і ясності, властивих цій мові від народження.
Розробник системи Turbo Pascal - фірма Borland International виникла в 1984 році і за порівняно короткий час неодноразово дивувала користувачів персональних ЕОМ своїми Turbo системами. Було випущено кілька версій Turbo Pascal: 3.0‚ 4.0‚ 5.0‚ 5.5‚ 6.0‚ 7.0‚ Pascal for Windows, Borland Pascal.
Головні особливості середовища Turbo Pascal:
широкий спектр типів даних‚ можливість обробки рядкових та структурних типів даних;
достатній набір операторів управління розгалуженнями та циклами;
добре розвинутий апарат підпрограм та зручні конструкції роботи з
файлами;
великі можливості управління усіма ресурсами ПЕОМ;
різноманітні варіанти стикування з мовою Асемблера;
підтримка ідей об'єктно-орієнтованого програмування (ООП).
Саме з огляду на ці особливості програмна реалізація курсового проекту було здійснено в середовищі Turbo Pascal.
Курсовий проект складається зі вступу, двох розділів, висновків, списку використаної літератури, графічної частини та додатків. Текст пояснювальної записки набрано та роздруковано з використанням текстового редактора Word. Графічна частина виконана з допомогою графічного редактора Visio.
1. Теоретична частина
1.1 Постановка задачі
Нехай дано систему п лінійних алгебраїчних рівнянь з п змінними
![]() (I=1.2…..n) (1)
(I=1.2…..n) (1)
Систему (1) можна записати у вигляді одного матричного рівняння
AX=B, (2)
де
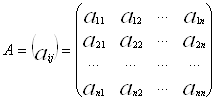
матриця коефіцієнтів ![]() (індекс і вказує рівняння, якому належить коефіцієнт, а індекс j – змінну, при якій він стоїть),
(індекс і вказує рівняння, якому належить коефіцієнт, а індекс j – змінну, при якій він стоїть),
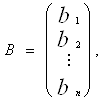
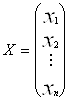 ,
,
відповідно стовпець вільних членів і стовпець змінних.
Упорядкована сукупність п чисел ![]() , яка, будучи підставленою в систему (1) замість
, яка, будучи підставленою в систему (1) замість ![]() , перетворює всі рівняння в правильні числові рівності, називається розв’язком системи (1)
, перетворює всі рівняння в правильні числові рівності, називається розв’язком системи (1)
![]()
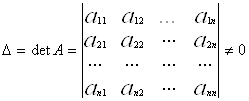
Методи розв’язування систем лінійних рівнянь можна поділити на дві групи: точні й ітераційні.
Точними називають такі методи, які дають змогу знайти точний розв’язок системи (1) за допомогою виконання скінченої кількості арифметичних операцій у припущенні, що всі обчислення виконуються точно (без округлень), а коефіцієнти системи і вільні члени – точні числа. Але на практиці всі обчислення виконуються з обмеженою кількістю десяткових розрядів, а ірраціональні коефіцієнти і вільні члени, якщо такі є, замінюються раціональними числами. Тому в процесі обчислення вдаються до округлень, а це означає, що розв’язки, які обчислюються за точними методами, фактично є наближеними числами з певними похибками (похибками округлень). До точних належать метод Гаусса, метод квадратних коренів, правило Крамера, сюди ж належить метод Жордана-Гаусса.
Інтераційними називають такі методи, які дають змогу знайти наближений розв’язок системи (1) із заздалегідь вказаною точністю шляхом виконання скінченої кількості арифметичних операцій, хоч самі обчислення можуть проводитись і без округлень, а коефіцієнти і вільні члени системи бути точними числами.
У процесі вивчення різних питань економіки, природознавства, техніки тощо доводиться розв’язувати системи алгебраїчних рівнянь. Зокрема, до таких систем зводиться чисельне розв’язування лінійних, диференціальних та інтегральних рівнянь. У таких системає коефіцієнти і вільні члени рівнянь – числа наближені. А це веде до появи додаткових (так званих неусуваних) похибок.
Якщо систему рівнянь у пам’яті машини записати навіть точно, то в процесі її розв’язування ЕОМ обов’язково виникнуть похибки округлень, які не можуть не вплинути на точність розв’язку. Проте, якщо матриця А системи (2) майже вираджена то можна сподіватися, що малі зміни в коефіцієнтах і (або) вільних членах також призведуть до значних змін у її розв’язку.
Якщо малі збурення коефіцієнтів і (або) вільних членів системи (1) дуже збурюють її розв’язок, то таку систему рівнянь називають погано обумовленою. Наприклад, якщо малі збурення коефіцієнтів і (або) вільних членів системи (1) мало збурюють її розв’язок, то таку систему називають добре обумовленою. Прикладом погано обумовленої є, наприклад, система вигляду:
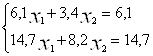 (3)
(3)
розв’язком якої є пара (1;0). Якщо число 6,1 у правій частині першого рівняння системи (3) змінити на 0,02, то система
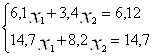
матиме розв’язком пару (5,1;-7,35). Отже, мале збурення (меньше 0,33%) одного з вільних членів системи (3) зовсім змінило розв’язок системи.
На щастя, на практиці системи рівнянь, погано обумовлені, зустрічаються дуже рідко.
Похожие работы
... , ary2s Типы данных для переменных, в которых хранятся значения коэффициентов системы Unit2 Gauss1 Процедура для решения системы линейных уравнений методом Гаусса Unit2 Gaussj Процедура для решения системы линейных уравнений методом Жордана-Гаусса Unit2 i,j,l Счетчики Unit1 prover Промежуточная переменная типа String, используется для проверки наличия букв среди коэффициентов ...
... на місце вектора А3 вводимо вектор А1 та знову робимо перерахунок системи в таблиці 2 за методом Жордана-Гаусса, взявши за провідний елемент а11 = 1,5. Таблиця 3. Третій крок симплекс-методу i Б Сб сk 3 2 0 0 A0 A1 A2 A3 A4 1 A1 3 1 1 0 0,666667 -0,33333 2 A2 2 2 0 1 -0,33333 0,66667 Dk 7 0 0 1,33333 0,33333 Таким чином ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
... на t3 часов. Прибыль от реализации единицы готового изделия А составляет a рублей, а изделия В - b рублей. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу простым симплекс-методом. Дать геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами. а1 = 1 b1 = 5 t1 = 10 a = 2 а2 = 3 b2 = 2 t2 ...




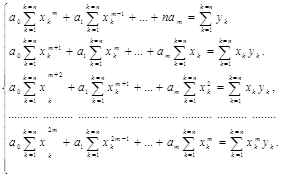
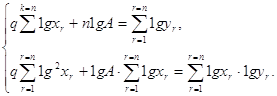
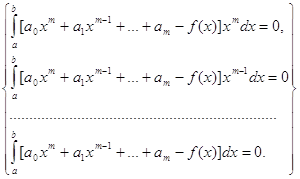
0 комментариев