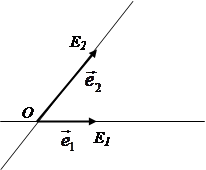
Применение композиций движений пространства к решению задач

1.5. Применение композиций движений пространства к решению задач

Аппарат движений пространства, а в частности композиции движений пространства, можно эффективно применять для решения геометрических задач.

Задача 11. Докажите, что биссектрисы двух плоских углов трехгранного угла DABC и биссектриса угла, смежного с третьим плоским углом, лежат в одной плоскости.

Решение. Пусть DE, DF – биссектрисы плоских углов ADB и BDC, DH – биссектриса угла, смежного с углом ADC, т.е. ÐDAE=ÐEDC, ÐBDF=ÐFDC, ÐCDH=ÐHDK (рис.11).

			D		K				H
A
								C
E						F
			B

Рис. 11

Рассмотрим композицию f трех осевых симметрий: f=S_DH◦S_DF◦S_DE. Движение f – это движение первого рода, как композиция движений первого рода. К тому же композиция S_DH◦S_DF◦S_DE отображает прямую AK на себя, точка D при этом неподвижна. Следовательно, рассматриваемая композиция есть осевая симметрия.

Воспользовавшись выводами, полученными в задаче 8 для случая с пересекающимися осями симметрий, можно сказать, что прямые DE, DF и DH лежат в одной плоскости.

Задача 12. Через вершину D прямого трехгранного угла DABC внутри его проведен луч DO. Доказать, что выполняется неравенство:

Ð(DO, DA)+Ð(DO, DB)+Ð(DO, DC)<180°.

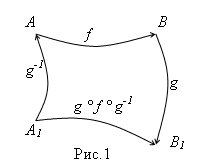
Решение. Обозначим через DE, DF и DH лучи, симметричные лучу DO относительно прямых DA, DB и DC соответственно (рис. 12). Поскольку трехгранный угол DABC – прямой, то прямые DB и DC перпендикулярны, и S_DC◦S_DB=S_DA (как композиция двух поворотов). Рассмотрим образ луча DF после применения симметрии S_DA:

S_DA(DF)=(S_DC◦S_DB)(DF)=S_DC(DO)=DH, кроме того S_DA(DO)=DE.

Следовательно, Ð(DO, DF)=Ð(DE, DH). Аналогично можно доказать, что Ð(DO, DE)=Ð(DF, DH) и Ð(DO, DH)=Ð(DE, DF).

D

H

E

C

A

O

B

F

Рис. 12

Оценим искомую сумму углов, учитывая полученные равенства:

Ð(DO, DA)+Ð(DO, DB)+Ð(DO, DC) =

= Ð(DO,DE) + Ð(DO,DF) + Ð(DO,DH) = ( Ð(DF,DH) + Ð(DE,DH) +

+ Ð(DE,DF) ). Лучи DE, DF и DH являются ребрами трехгранного угла DEFH, а значит сумма Ð(DF,DH)+Ð(DE,DH)+Ð(DE,DF)<360°.

Таким образом, Ð(DO, DA)+Ð(DO, DB)+Ð(DO, DC)<180°.

§2. Композиции подобий и аффинных преобразований пространства

 

Среди преобразований пространства выделяют также преобразования, не сохраняющие расстояния между точками, - это подобия, гомотетии как частный случай подобий, и аффинные преобразования.

Задача 13. Найти композицию гомотетии и переноса пространства: ◦H_O^k.

Решение. Рассмотрим образ произвольной точки X после применения искомой композиции. Пусть X₁ – образ X после применения H_O^k: H_O^k(X)=X₁, а точка X₂ – образ X₁ после применения переноса: (X₁)= X₂. Через центр гомотетии O проведем прямую n параллельную прямой, содержащую вектор  (рис. 13).

n

S1

S

O

X

X1

X2

 Рис. 13

 Найдем образ точки пересечения построенной прямой n и прямой XX₂ при гомотетии H_O^k: H_O^k(S)=S₁. Тогда =, поэтому точка S при заданной композиции неподвижна, кроме того, не зависит от выбора точки X. С учетом того, что =k, =k(т.к. треугольники SOX и X₁XX₂ подобны), искомая композиция является гомотетией H_S^k.

Таким образом, ◦H_O^k=H_S^k. (4)

Задача 14. Найти композицию двух гомотетий пространства.

Решение. Рассмотрим образ произвольной точки X после применения композиции гомотетий f=H_B^m◦H_A^k. Пусть H_A^k (X)=X₁, т.е. по определению гомотетии =k, H_B^m(X₁)=X₂, т.е. =m (рис.14). Найдем образ точки A после применения гомотетии H_B^m: H_B^m(A)=A₁, т.е. =m. Таким образом, отрезок A₁X₂ – это образ отрезка AX после применения данной композиции, при этом прямые, содержащие эти отрезки параллельны (это следует из подобия треугольников ABX₁ и A₁BX₂). Если прямые AA₁ и XX₂ пересекаются (обозначим точку их пересечения C), тогда, рассматривая подобные треугольники ACX и A₁CX₂ , выразим вектор :

==, при этом =m=km.

				X2
							A1
			C
					B
A
	X
				X1

Рис. 14

Следовательно, = km. Точка C не зависит от выбора точки X, значит композиция f является гомотетией с центром в C:

H_B^m◦H_A^k=H_C^km. (5)

 Если прямые AA₁ и XX₂ не пересекаются, т.е. =, то km=1, следовательно, композиция f есть перенос пространства:

H_B^m◦H_A^k=. (6)

Все эти рассуждения верны и для совпадающих центров исходных гомотетий.

Задача 15. Найти композицию двух подобий пространства.

Решение. Так как любое подобие пространства можно представить в виде композиции поворота и гомотетии, центр которой лежит на оси поворота, то, учитывая ассоциативность этого представления, будем находить требующуюся композицию в следующем виде: f=H_B^m◦R_h^b◦R_l^a◦H_A^k.

Рассмотрим несколько случаев.

1)Если оси поворотов h и l параллельны, и при этом сумма углов не равна 2p, то композиция поворотов является поворотом R_n^a+b , где ось n параллельна исходным осям h, l. Тогда f=H_B^m◦R_n^a+b◦H_A^k, при этом композиция R_n^a+b◦H_A^k является по определению подобием, а значит, эта композиция может быть представлена в виде H_D^k◦R_p^a+b. И равенство f=H_B^m◦R_n^a+b◦H_A^k эквивалентно равенству f=H_B^m◦H_D^k◦R_p^a+b . По формуле (5) H_B^m◦H_D^k=H_C^km(при km¹1), значит f=H_C^km◦R_p^a+b, а это по определению подобие. При km=1 по формуле (6) H_B^m◦H_D^k=, и f=◦R_p^a+b, а это, в общем случае, винтовое движение.

 2)Если же при параллельных осях данных поворотов h и l сумма углов равна 2p, то композиция поворотов R_h^b◦R_l^a является переносом пространства , и в этом случае f=H_B^m◦◦H_A^k. Композиция ◦H_A^k согласно выводу (4) есть гомотетия с центром в некоторой точке C с коэффициентом k: ◦H_A^k=H_С^k. Следовательно, f=H_B^m◦H_С^k, а это гомотетия пространства (согласно формуле (5)) или параллельный перенос пространства (по (6) ).

3)Если прямые h и l пересекаются, то композиция поворотов R_h^b◦R_l^a является поворотом R_n^w. И нахождение композиции f сводится к случаю 1.

4)Если оси h и l скрещиваются, то композиция поворотов R_h^b◦R_l^a является винтовым движением, следовательно, композиция R_h^b◦R_l^a◦H_A^k является подобием пространства, которое можно представить композицией поворота и гомотетии: R_h^b◦R_l^a◦H_A^k=R_n^w◦H_Сⁿ. Тогда нахождение f сводится к случаю 1.

Таким образом, композиция двух подобий пространства, произведение коэффициентов которых не равно 1, есть подобие пространства или гомотетия (в случае параллельных осей поворотов и сумме их углов 2p), в тривиальном случае, когда произведение коэффициентов исходных подобий равно 1, эта композиция может вырождаться в винтовое движение пространства или перенос.

Аналогичная ситуация обстоит и с композицией аффинных преобразований пространства, т.е. в общем случае композиция двух аффинных преобразований пространства также является аффинным преобразованием.

Литература

 

1. Гусев В. А., Тхамафокова С. Т. Преобразования пространства. Москва: «Просвещение», 1979.

2. Понарин Я. П. Геометрия: Учебное пособие. Ростов-на-Дону: «Феникс», 1997.

3.  Понарин Я. П. Преобразования пространства. Киров: 2000.

4. Скопец З. А. Геометрические миниатюры. Москва: «Просвещение», 1990.