Пусть X - множество всех точек прямой ![]() , плоскости
, плоскости ![]() или трехмерного пространства
или трехмерного пространства ![]() . Обозначим через d(P, Q) расстояние между точками P и Q множества X. Отображение f: X ® X f(P) = P называется перемещением, если для всех P и Q d(P, Q) = d(P , Q ).
. Обозначим через d(P, Q) расстояние между точками P и Q множества X. Отображение f: X ® X f(P) = P называется перемещением, если для всех P и Q d(P, Q) = d(P , Q ).
Примеры.
1. Пусть в ![]() выбрана правая декартова прямоугольная система координат (x, y) с началом О. Поворот
выбрана правая декартова прямоугольная система координат (x, y) с началом О. Поворот ![]() плоскости на угол j вокруг точки О задается формулами R =
плоскости на угол j вокруг точки О задается формулами R = 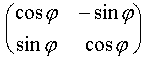 R. Здесь P=
R. Здесь P= ![]() , R =
, R = ![]() . Очевидно, поворот является перемещением плоскости.
. Очевидно, поворот является перемещением плоскости.
Отметим, что ![]() (О) =О, то есть точка О остается неподвижной при повороте. Аналогично, в
(О) =О, то есть точка О остается неподвижной при повороте. Аналогично, в ![]() можно рассмотреть поворот
можно рассмотреть поворот ![]() на угол j вокруг оси, заданной единичным вектором v и точкой О. Легко проверить, что это перемещение задается формулой: R =Rcosj + (R´ v )sinj +v (1-cosj )(R× v ) . Все точки оси поворота являются неподвижными.
на угол j вокруг оси, заданной единичным вектором v и точкой О. Легко проверить, что это перемещение задается формулой: R =Rcosj + (R´ v )sinj +v (1-cosj )(R× v ) . Все точки оси поворота являются неподвижными.
2. Перемещением будет и параллельный перенос ![]() на вектор v , Очевидно, P= R+v . Неподвижных точек перенос не имеет.
на вектор v , Очевидно, P= R+v . Неподвижных точек перенос не имеет.
3. Пусть l некоторая прямая в ![]() . (Зеркальное) отражение
. (Зеркальное) отражение ![]() относительно этой прямой является перемещением. Если в декартовой прямоугольной системе координат уравнение прямой имеет вид y = tg(j /2) x , то отражение задается формулой : P=
относительно этой прямой является перемещением. Если в декартовой прямоугольной системе координат уравнение прямой имеет вид y = tg(j /2) x , то отражение задается формулой : P= 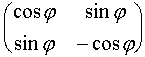 R . Аналогично, если p некоторая плоскость в
R . Аналогично, если p некоторая плоскость в ![]() , то отражение
, то отражение ![]() относительно этой плоскости будет перемещением. Если n единичный вектор нормали к плоскости p , проходящей через начало координат, то R = R - 2(R× n)n .
относительно этой плоскости будет перемещением. Если n единичный вектор нормали к плоскости p , проходящей через начало координат, то R = R - 2(R× n)n .
Переносы и отражения (примеры 2 и 3) можно рассматривать и в ![]() .
.
4. Композиция U* V (последовательное выполнение ) двух перемещений U и V снова будет перемещением: (U* V)(P) = U(V(P)). Например, ![]() =
= ![]() *
* ![]() = I - тождественное перемещение.
= I - тождественное перемещение.
Теорема 1
Пусть f: X ® X - перемещение, A, B, C, D - точки X, f(A) = A и т.д. Если AB = CD (как свободные векторы), то A B = C D .
Доказательство.
Достаточно проверить, что в условиях теоремы четырехугольник A B D C является параллелограммом. Пусть О точка пересечения диагоналей AD и BC. Принадлежность точки О отрезку АD равносильно равенству: d(A, O) + d(O, D) = d(A, D). Поскольку для образов этих точек имеет место аналогичное равенство d(A , O ) + d(O , D ) = d(A , D ) , мы видим, что O лежит на отрезке A D и делит его пополам, поскольку d(A , O ) = d(A ,O) = 1/2 d(A ,D) = 1/2 d(A , D ) . Аналогично, O лежит на C D и делит его пополам. Следовательно, A B D C - параллелограмм.
Из теоремы 1 следует, что если ![]() - пространство свободных векторов, то для всякого перемещения f: X ® X определено отображение: f*: V ® V.
- пространство свободных векторов, то для всякого перемещения f: X ® X определено отображение: f*: V ® V.
Отметим, что если О - некоторая фиксированная точка X, то для любой точки P точка f(P) получается из O переносом на вектор f*(OP). Отсюда вытекает, что перемещение f однозначно определяется отображением f* и точкой O .
Теорема 2.
Отображение f* является линейным оператором в V и сохраняет скалярное произведение.
Доказательство.
Свойство f*(u + v) = f*(u) +f*(v) следует из определения сложения векторов : если u = AB , v = BC , то u + v = AC. Так как при перемещении любой треугольник ABC переходит в равный треугольник, то сохраняются не только длины, но и углы между векторами, а значит и скалярное произведение. Наконец, использую сохранение скалярного произведения, имеем: ![]() 2
2![]() +
+ ![]() =0. Следовательно, f*(l v) = l f*(v) , то есть отображение f* линейно.
=0. Следовательно, f*(l v) = l f*(v) , то есть отображение f* линейно.
Следствие
Отображение ![]() евклидова пространства V, обладающее свойством
евклидова пространства V, обладающее свойством ![]() является линейным оператором и сохраняет скалярное произведение.
является линейным оператором и сохраняет скалярное произведение.
Как известно, оператор в конечномерном пространстве определяется своей матрицей. Матрица A оператора, сохраняющего скалярное произведение, называется ортогональной и имеет следующие свойства:
Матрица А невырождена, более того det(A) =Кроме того, известны простейшие формы ортогональных матриц в ортонормированном правом базисе. Эти простейшие формы указаны в следующей таблице:
| dimV | det(A) = 1 | Название | det(A) = -1 | Название |
| 1 | I = (1) | Тождест-венный оператор | s = (-1) | Отраже-ние |
| 2 |
| Поворот на угол j |
| Отраже-ние |
| 3 |
| Поворот на угол j вокруг OZ |
| Зеркаль-ный пово-рот |
Замечание 1.
Учитывая связь между перемещением f и оператором f*, можно утверждать, что в подходящей декартовой системе координат имеет место формула:
R = АR + v , где А - одна из матриц из таблицы, а v - некоторый вектор. Следовательно, всякое перемещение f имеет обратное ![]() , которое задается формулой R =
, которое задается формулой R = ![]() (R - v ) =
(R - v ) = ![]() R -
R - ![]() v. Поскольку матрица
v. Поскольку матрица ![]() - ортогональна, обратное отображение также является перемещением. Отметим еще, что для всякой ортогональной матрицы P и любого вектора w преобразование R = PR + w является перемещением.
- ортогональна, обратное отображение также является перемещением. Отметим еще, что для всякой ортогональной матрицы P и любого вектора w преобразование R = PR + w является перемещением.
Замечание 2.
Имеется существенное различие между математическим понятием перемещения и физическим понятием движения. Во втором случае имеется в виду непрерывное во времени изменение положения точки, в то время как в первом фиксируются только ее начальное и конечное положения.
Перемещения с det(A) = 1 можно представлять себе и как движения, в то время как при det(A)= -1 такое представление невозможно, если оставаться в пределах исходного пространства X.
3. Классификация перемещений. Напомним, что нам уже известны некоторые перемещения. Перемещениями прямой ![]() являются тождественное преобразование I, перенос
являются тождественное преобразование I, перенос ![]() на вектор v и отражение
на вектор v и отражение ![]() относительно точки О .
относительно точки О .
Для случая плоскости ![]() перемещениями будут уже упомянутые I и
перемещениями будут уже упомянутые I и ![]() , а также поворот
, а также поворот ![]() вокруг точки О на угол j и отражение
вокруг точки О на угол j и отражение ![]() относительно прямой l . Определим дополнительно скользящее отражение
относительно прямой l . Определим дополнительно скользящее отражение ![]() как комбинацию отражения относительно прямой l с переносом на вектор v½ ½ l .
как комбинацию отражения относительно прямой l с переносом на вектор v½ ½ l .
Наконец, для пространства ![]() мы имеем перемещения I и
мы имеем перемещения I и ![]() , а, кроме того поворот
, а, кроме того поворот ![]() вокруг оси, заданной точкой О и единичным направляющим вектором w на угол j и отражение
вокруг оси, заданной точкой О и единичным направляющим вектором w на угол j и отражение ![]() относительно плоскости p . Определим дополнительно зеркальный поворот
относительно плоскости p . Определим дополнительно зеркальный поворот ![]() как комбинацию отражения относительно плоскости, заданной точкой О и вектором нормали n с поворотом
как комбинацию отражения относительно плоскости, заданной точкой О и вектором нормали n с поворотом![]() и скользящее отражение - композицию отражения .
и скользящее отражение - композицию отражения . ![]() относительно плоскости p и переноса на вектор v½ ½ p . Наконец, определим винтовое перемещение
относительно плоскости p и переноса на вектор v½ ½ p . Наконец, определим винтовое перемещение ![]() как комбинацию поворота
как комбинацию поворота ![]() и параллельного переноса на вектор hw .
и параллельного переноса на вектор hw .
Отметим, что некоторые из указанных выше перемещений являются частными случаями других. Например, тождественное перемещение можно рассматривать как перенос на нулевой вектор (или как поворот на нулевой угол), отражение ![]() является частным случаем скользящего отражения
является частным случаем скользящего отражения ![]() при v = 0 и т. д.
при v = 0 и т. д.
Теорема 3 .
Каждое перемещение f в ![]() (n = 1, 2, 3 ) суть одно из следующих :
(n = 1, 2, 3 ) суть одно из следующих :
Доказательство.
Как уже отмечалось, можно выбрать такой ортонормированный базис, что перемещение f имеет вид R = АR + v , где v - некоторый вектор. Если изменить начало координат : R = r + u , R = r + u , получаем: r = Ar + v , где v = Au -u +v = (A - E)u + v .Мы видим, что если число 1 не является собственным значением матрицы А (или, если угодно, оператора f*) , то можно выбрать u так, что в новой системе координат v = 0 . (Поскольку матрица A - E невырождена). Тем самым утверждение теоремы доказано при n=1 и при n=2 в случае det(A) = 1 (так как собственные значения ![]() суть exp(
суть exp(![]() ij )¹ 1 при j ¹ 2 p n ).
ij )¹ 1 при j ¹ 2 p n ).
В случае матрицы ![]() можно добиться, чтобы v =
можно добиться, чтобы v = ![]() , что приводит к скользящему отражению
, что приводит к скользящему отражению ![]() . Для матрицы
. Для матрицы ![]() при j ¹ 2 p n получаем v =
при j ¹ 2 p n получаем v = ![]() , и мы приходим к винтовому перемещению
, и мы приходим к винтовому перемещению ![]() . (При j =2 p n мы приходим к переносу). Наконец, для
. (При j =2 p n мы приходим к переносу). Наконец, для ![]() при j ¹ 2 p n можно считать v = 0 , что приводит к зеркальному повороту
при j ¹ 2 p n можно считать v = 0 , что приводит к зеркальному повороту ![]() , а при j =2 p n - v =
, а при j =2 p n - v = ![]() и получается скользящее отражение
и получается скользящее отражение ![]() .
.
Замечание. ( о параметрах перемещений)
Параметр ![]() для поворота плоскости
для поворота плоскости ![]() будем считать изменяющимся mod 2 p т. е.
будем считать изменяющимся mod 2 p т. е. ![]() =
= ![]() . Такое же соглашение будем использовать и для винтового перемещения
. Такое же соглашение будем использовать и для винтового перемещения ![]() при h > 0. Если же h = 0 , и речь идет о повороте в пространстве, надо учитывать, что
при h > 0. Если же h = 0 , и речь идет о повороте в пространстве, надо учитывать, что ![]() =
= ![]() . В частности,
. В частности, ![]() =
= ![]() (отражение относительно прямой параллельной v и проходящей через О). Аналогично,
(отражение относительно прямой параллельной v и проходящей через О). Аналогично, ![]() =
= ![]() . Если при этом j = p это преобразование не зависит от вектора n и является отражением относительно точки О.
. Если при этом j = p это преобразование не зависит от вектора n и является отражением относительно точки О.
Теорема 4
Если f и g два перемещения X, а f*, g* - соответствующие операторы в V, то (f· g)* = f*g*(Символом · обозначена композиция перемещений).
Доказательство.
Используем координатную форму записи: f( R) = AR + v, g( R) = BR + w. Тогда: (f· g)( R) = f( (g( R)) = f( BR + w) = A( BR +w) +v = ( AB)R + ( Aw + v). Следовательно, (f· g)* = AB = f*g*.
Следствие.
Композиция двух перемещений с определителями одного знака имеет определитель (+1); если знаки определителей противоположны, композиция имеет определитель (-1).
Вычисление композиции перемещений пространства ![]() не вызывает затруднений. Отметим только, что
не вызывает затруднений. Отметим только, что ![]() ·
· ![]() =
= ![]() ,где v =2AB.
,где v =2AB.
Для случая пространства ![]() удобно использовать комплексные числа. Отождествляя их с точками плоскости, получаем удобный способ записи перемещений. Например, поворот
удобно использовать комплексные числа. Отождествляя их с точками плоскости, получаем удобный способ записи перемещений. Например, поворот ![]() можно записать в виде: z ®
можно записать в виде: z ® ![]() z + c. Точка О является неподвижной и соответствующее комплексное число
z + c. Точка О является неподвижной и соответствующее комплексное число ![]() находится из уравнения
находится из уравнения ![]() =
= ![]()
![]() + с, откуда
+ с, откуда ![]() = с/(1-
= с/(1-![]() ). Таким образом,
). Таким образом, ![]() Отметим, что
Отметим, что ![]() =
=![]() при j + y ¹ 0 (mod 2 p ) . В то же время при j + y = 0 указанная композиция будет переносом на вектор AD, где D =
при j + y ¹ 0 (mod 2 p ) . В то же время при j + y = 0 указанная композиция будет переносом на вектор AD, где D = ![]() .
.
Преобразование z® ![]() +c является скользящим отражением относительно прямой Im(
+c является скользящим отражением относительно прямой Im(![]() = 0 на вектор 0,5 (с +
= 0 на вектор 0,5 (с + ![]() ). Если прямая l проходит через точку
). Если прямая l проходит через точку ![]() и ее направляющий вектор (рассматриваемый как комплексное число) имеет аргумент
и ее направляющий вектор (рассматриваемый как комплексное число) имеет аргумент ![]() , то перемещение
, то перемещение ![]() можно записать в виде
можно записать в виде ![]()
Композиция двух скользящих отражений относительно пересекающихся прямых будет поворотом. В то же время, если прямые параллельны, композиция - перенос.
Похожие работы
... до того, что начали овеществлять время и даже придумали частицу времени – хронон. С позиций нового (или восстановленного древнего) определения времени теряют право на жизнь преобразования Лоренца и ставшая уже привычной четырехмерная размерность пространства-времени, о чем будет показано ниже. На смену им приходят новые преобразования и полностью симметричное шестимерное пространство-время (хотя ...
... и сохраняет операцию. По построению l сюръективно. Инъективность вытекает из закона правого сокращения: . Сохранение операции фактически уже было установлено выше: . Следствие. Любая абстрактная группа изоморфна группе преобразований некоторого множества (Достаточно взять G=H и рассмотреть левые сдвиги). Для случая конечных групп получается теорема Кэли: Любая группа из n элементов ...
... уравнение получается из другого с помощью преобразований Галилея. Действительно, согласно этим преобразованиям: так как очевидно dv/dt = 0 (скорость v постоянна). Самыми фундаментальными объектами в физике являются точки и волны. Поэтому интересно посмотреть, а будет ли инвариантно относительно преобразований Галилея волновое уравнение, скажем, для простоты, одномерное волновое уравнение ( ...
... выстраивается эффективная модель структурно-инвестиционной политики, адекватная постиндустриальной модели развития национальной экономики. Управление структурно-инвестиционными преобразованиями в промышленном секторе должно базироваться на системе взаимодействия государственных, общественных, корпоративных институтов с целью обеспечения наиболее полного использования инвестиционного потенциала ...
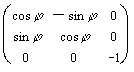
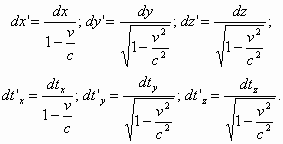
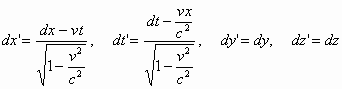
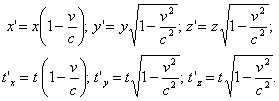
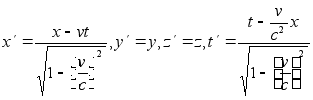
0 комментариев