Навигация
Композиции центральных симметрий пространства
25788
знаков
28
таблиц
10
изображений
1.2. Композиции центральных симметрий пространства
Задача 4. Найти композицию: а) двух центральных симметрий пространства, б) центральной симметрии и переноса, в) трёх центральных симметрий пространства.
Решение. а) Найдём композицию центральных симметрий пространства с центрами A и B. Для этого найдём образ произвольной точки M после применения композиции ZB◦ZA:
(ZB◦ZA)(M)=P (рис. 4).
| | M | |||||||
| A | ||||||||
| P | ||||||||
| B | ||||||||
| N |
Рис. 4
Для треугольника MNP имеет место равенство: 
=2
. Точки A и B заданы, следовательно, вектор - постоянный, и искомая композиция двух центральных симметрий ZB◦ZA есть параллельный перенос на вектор 2:
ZB◦ZA=
. (1)
б) Найдем композицию центральной симметрии ZO и переноса 
в пространстве. Представим перенос как композицию двух центральных симметрий: =ZB◦ZO, где 
=
. Следовательно, ◦ZO=(ZB◦ZO)◦ZO. Это равенство эквивалентно равенству:
◦ZO=ZB .
(2)
Таким образом, композиция центральной симметрии ZO и переноса есть центральная симметрия ZO , центр которой определяется условием =.
в) Найдем композицию трех центральных симметрий пространства f=ZC◦ZB◦ZA. Композицию ZC◦ZB представим в виде переноса в соответствии с выводом (1): ZC◦ZB=
. Тогда искомая композиция будет иметь следующий вид: f=◦ZA. Воспользовавшись выводом (2), заметим, что правая часть равенства есть центральная симметрия ZO, центр О которой определяется условием 
=
. Таким образом, композиция трех центральных симметрий пространства является центральной симметрией.
Пользуясь ассоциативностью композиции и выводами, полученными ранее, обобщим:
1) композиция четного числа центральных симметрий пространства является переносом;
2) композиция нечетного числа центральных симметрий пространства является центральной симметрией.
Задача 5. Найти композицию центральных симметрий пространства относительно последовательно взятых вершин параллелограмма ABCD.
Решение. Требуется найти композицию f=ZD◦ZC◦ZB◦ZA (рис. 5).
| | C | B | |||||||||
| D | A |
Рис. 5
Сгруппируем элементы композиции «удобным» образом и воспользуемся выводом (1) предыдущей задачи:
f=(ZD◦ZC)◦(ZB◦ZA)=
◦. Векторы 
и 
являются противоположными, поскольку ABCD есть параллелограмм, следовательно искомая композиция является тождественным преобразованием E.
Обобщим эту задачу на случай четырех произвольных точек.
Задача 6. Найти композицию центральных симметрий пространства относительно четырех произвольных точек.
Решение. Требуется найти композицию f=ZE◦ZC◦ZB◦ZA (рис. 6). Воспользуемся результатом предыдущей задачи, для этого построим, например, в плоскости BCD точку D такую, что четырехугольник BCED является параллелограммом.
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| A |
|
|
|
|
| B |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
| C |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
| D |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
| E |
|
|
|
|
|
|
|
|
|
|
|
Рис. 6
Тогда равенству f=ZE◦ZC◦ZB◦ZA эквивалентно равенство f=ZD◦ZD◦ZE◦ZC◦ZB◦ZA. Композиция ZD◦ZE◦ZC◦ZB есть тождественное преобразование, т.к. BCED – параллелограмм. И искомая композиция имеет вид f=ZD◦ZA , а это перенос пространства 
(согласно выводу (1) ).
Похожие работы
... точка А сместилась в направлении f(l). Следовательно, в силу произвольности точки А, искомая трансформация есть косое сжатие с осью f(q), направлением f(l) и коэффициентом k. 17. Решение задач с помощью трансформации преобразований Задача 1. Даны правильные одинаково ориентированные треугольники OAB, OCD, OEF. Доказать, что середины M, N, P соответственно отрезков BC, DE, AF являются вершинами ...
... в сопряжённых комплексных координатах 1.1. Определение аффинного преобразования Введём определение аффинного преобразования евклидовой плоскости в сопряжённых комплексных координатах. Преобразование евклидовой плоскости называется аффинным, если оно отображает каждую прямую на прямую. [1] 1.2. Формула аффинного преобразования Мы хотим построить теорию аффинных преобразований с помощью ...
... вследствие объективных причин (болезнь детей) в эксперименте принимало участие 5 детей, проявлявших особый интерес к занятиям изобразительной деятельностью. Опытно - экспериментальную работу по развитию декоративного творчества детей старшего дошкольного возраста средствами декоративной композиции мы строили в три этапа: 1 - констатирующий эксперимент; 2 - формирующий эксперимент; 3 - итоговый ...
... идет о повороте в пространстве, надо учитывать, что = . В частности, = (отражение относительно прямой параллельной v и проходящей через О). Аналогично, = . Если при этом j = p это преобразование не зависит от вектора n и является отражением относительно точки О. 4* Композиции 1. Теорема 4 Если f и g два перемещения X, а f*, g* - соответствующие операторы в V, то (f· g)* = f*g*( ...
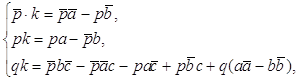
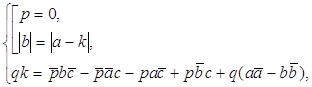
0 комментариев