Навигация
Иррациональные уравнения, которые решаются введением новой переменной
2.3 Иррациональные уравнения, которые решаются введением новой переменной
При решении различных видов уравнений: рациональных, тригонометрических, показательных часто используется метод введения новой переменной. Новая переменная в уравнениях иногда действительно очевидна, но иногда ее трудно увидеть, а можно выявить только лишь в процессе каких либо преобразований. Бывает полезно ввести не одну, а две переменные. Видим типичные случаи введения новых переменных в иррациональных уравнениях.
Пример 1. Решить уравнение ![]()
Решение. Введем новую переменную. Пусть ![]() ,
, ![]() , где
, где ![]() . Получаем, что
. Получаем, что ![]()
![]() .Тогда
.Тогда ![]() - не удовлетворяет условию
- не удовлетворяет условию ![]()
Выполним обратную замену. ![]()
О т в е т:{34}.
Пример 2. Решить уравнение ![]()
Решение. Уединение радикала и возведение в степень обеих частей уравнения привело бы к громоздкому уравнению. В то же время, если проявить некоторую наблюдательность, то можно заметить, что данное уравнение сводиться к квадратному. Действительно, умножим обе части заданного уравнения на 2, получим, что ![]()
![]()
![]()
![]()
Введем новую переменную. Пусть ![]() Получаем, что
Получаем, что ![]() . Тогда
. Тогда ![]() - не удовлетворяет условию
- не удовлетворяет условию ![]() ,
, ![]()
Выполним обратную замену. ![]()
![]() Тогда
Тогда ![]() ,
, ![]()
Т.к. исходное уравнение равносильно уравнению ![]() то проверка полученных корней не нужна.
то проверка полученных корней не нужна.
О т в е т: {-2;3,5}.
Пример 3. Решить уравнение ![]()
Решение. Преобразуем данное уравнение. ![]()
![]()
Введем новую переменную. Пусть, ![]() а
а ![]() Получаем, что
Получаем, что ![]() . Тогда
. Тогда ![]() - не удовлетворяет условию
- не удовлетворяет условию ![]() .
.
Выполним обратную замену. ![]() .
.
О т в е т:{1}.
2.4 Уравнения вида ![]() ,
, ![]() ,
, ![]()
Данные уравнения можно решить при помощи основного метода решения иррациональных уравнений (возведение в квадрат обеих частей уравнения), но иногда их можно решить и другими методами.
Рассмотрим уравнение ![]() (1). Пусть
(1). Пусть ![]() - корень уравнения (1). Тогда справедливо числовое равенство
- корень уравнения (1). Тогда справедливо числовое равенство ![]() . Найдем разность чисел
. Найдем разность чисел ![]() и
и ![]() , обозначив ее
, обозначив ее ![]() , и запишем данное равенство в виде
, и запишем данное равенство в виде ![]() (2).
(2).
Используя, что ![]() , запишем равенство (2) в виде
, запишем равенство (2) в виде ![]() . Данное равенство означает, что число
. Данное равенство означает, что число ![]() есть корень уравнения
есть корень уравнения ![]() (3).
(3).
Таким образом, уравнение (3) является следствием уравнения (1). Складывая эти два уравнения и умножая полученное уравнение на а, получим уравнение![]() (4), также являющееся следствием уравнения (1). Возведя уравнение (4) в квадрат и решив полученное уравнение, надо выполнить проверку найденных корней, т.е. проверить, являются ли его корни корнями уравнения (1).
(4), также являющееся следствием уравнения (1). Возведя уравнение (4) в квадрат и решив полученное уравнение, надо выполнить проверку найденных корней, т.е. проверить, являются ли его корни корнями уравнения (1).
Замечание. Отметим, что точно также доказывается, что уравнение (4) есть следствие уравнения ![]() .
.
Пример 1. Решить уравнение ![]() (5).
(5).
Решение. Разность подкоренных выражений ![]() и
и ![]() есть
есть
![]() .
. 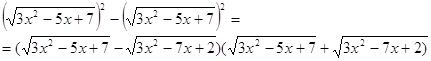 ,
,
то уравнение ![]() (6) является следствием исходного уравнения. Тогда, складывая уравнения (5) и (6), получим уравнение
(6) является следствием исходного уравнения. Тогда, складывая уравнения (5) и (6), получим уравнение ![]() (7), также являющееся следствием исходного уравнения (5). Возведем обе части уравнения (6) в квадрат, получим уравнение
(7), также являющееся следствием исходного уравнения (5). Возведем обе части уравнения (6) в квадрат, получим уравнение ![]() (8), также являющееся следствием исходного уравнения. Решая уравнение (8), получаем, что
(8), также являющееся следствием исходного уравнения. Решая уравнение (8), получаем, что ![]() ,
, ![]()
Проверкой убеждаемся, что оба этих числа являются корнями исходного уравнения.
О т в е т:![]() .
.
Замечание. Уравнение вида ![]() можно решать умножением обеих частей уравнения на некоторое выражение, не принимающее значение ноль (на сопряженное левой части уравнения т.е.
можно решать умножением обеих частей уравнения на некоторое выражение, не принимающее значение ноль (на сопряженное левой части уравнения т.е. ![]()
Пример 2. Решить уравнение ![]() (8).
(8).
Решение. Т.к. ![]() , то умножим обе части уравнения на выражение
, то умножим обе части уравнения на выражение ![]() , являющееся сопряженным левой части уравнения (8).
, являющееся сопряженным левой части уравнения (8). ![]()
![]() . После приведения подобных слагаемых получаем уравнение
. После приведения подобных слагаемых получаем уравнение ![]() (9), равносильное исходному, т.к. уравнение
(9), равносильное исходному, т.к. уравнение ![]() действительных корней не имеет. Складывая уравнения (8) и (9) получаем, что
действительных корней не имеет. Складывая уравнения (8) и (9) получаем, что ![]() . Тогда
. Тогда ![]()
![]()
О т в е т:![]() .
.
Замечание. Также уравнения вида ![]() можно решать с помощью ОДЗ уравнения и равносильных переходов от одних уравнений к другим.
можно решать с помощью ОДЗ уравнения и равносильных переходов от одних уравнений к другим.
Пример 3. Решить уравнение ![]()
Решение. Найдем ОДЗ переменной х.
ОДЗ:![]() Следовательно,
Следовательно, ![]()
На ОДЗ обе части уравнения положительны, поэтому после возведения в квадрат получим уравнение: ![]() , равносильное для
, равносильное для ![]() уравнению
уравнению
![]()
Иногда решения уравнения можно найти, решая его на разных числовых промежутках.
Для любого ![]() имеем
имеем ![]() , а
, а ![]() . Следовательно, среди
. Следовательно, среди ![]() нет решений уравнения
нет решений уравнения ![]() .
.
Для ![]() имеем
имеем ![]() . Следовательно,
. Следовательно, ![]()
![]() для
для ![]() .
. ![]() . Тогда
. Тогда ![]() . Т.к.
. Т.к. ![]() , то
, то ![]() является корнем уравнения
является корнем уравнения ![]() , равносильному уравнению
, равносильному уравнению ![]() для этих х.
для этих х.
О т в е т: ![]() .
.
Пример 4. Решить уравнение ![]()
Решение. Преобразуем исходное уравнение. ![]()
Возведем обе части данного уравнения в квадрат.
![]()
Проверка показывает, что 5 является корнем исходного уравнения.
Замечание. Иногда значительно проще можно решать уравнения вида ![]() , если воспользоваться свойствами монотонности функций, а именно тем, что сумма двух возрастающих функций является возрастающей функцией, и всякая монотонная функция каждое свое значение принимает, лишь при одном значении аргумента. Действительно, функции
, если воспользоваться свойствами монотонности функций, а именно тем, что сумма двух возрастающих функций является возрастающей функцией, и всякая монотонная функция каждое свое значение принимает, лишь при одном значении аргумента. Действительно, функции ![]() и
и ![]() - возрастающие. Следовательно, их сумма - возрастающая функция.
- возрастающие. Следовательно, их сумма - возрастающая функция.
Значит, исходное уравнение, если имеет корень, то только один. В этом случае, учитывая, что ![]() , подбором легко найти, что 5 является корнем исходного уравнения.
, подбором легко найти, что 5 является корнем исходного уравнения.
О т в е т:{5}.
Пример 5. Решить уравнение ![]()
Решение. Если обе части исходного уравнения возвести в квадрат, то получится довольно сложное уравнение. Поступим по-другому: преобразуем уравнение к виду:

Решим неравенство системы.
![]()
![]()

Решением системы является множество:
![]() .
.
Решим уравнение системы.
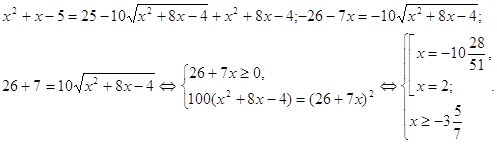
Убеждаемся, что 2 принадлежит множеству решений неравенства (рис.1).
Замечание. Если решать данное уравнение возведением обеих частей в квадрат, то необходимо выполнить проверку. 2 - целое число, поэтому при выполнении проверки трудностей не возникает. А что касается значения ![]() , то подстановка его в исходное уравнение приводит к весьма сложным вычислениям. Однако такой подстановки можно избежать, если заметить, что при этом значении правая часть уравнения
, то подстановка его в исходное уравнение приводит к весьма сложным вычислениям. Однако такой подстановки можно избежать, если заметить, что при этом значении правая часть уравнения ![]() принимает отрицательное значение:
принимает отрицательное значение: ![]() . Тогда как левая часть уравнения отрицательной быть не может. Таким образом,
. Тогда как левая часть уравнения отрицательной быть не может. Таким образом, ![]() не является корнем уравнения - следствия данного уравнения. Тем более, это значение не может быть корнем исходного уравнения. Итак, корень уравнения - число 2.
не является корнем уравнения - следствия данного уравнения. Тем более, это значение не может быть корнем исходного уравнения. Итак, корень уравнения - число 2.
О т в е т:{2}.
Пример 6. Решить уравнение ![]()
Решение. Найдем ОДЗ переменной х.
ОДЗ: 
Следовательно, ![]()
Для любых значений ![]() из ОДЗ, удовлетворяющих условию
из ОДЗ, удовлетворяющих условию ![]() , т.е. для
, т.е. для ![]() из промежутка
из промежутка ![]() левая часть уравнения отрицательна, а первая – неотрицательна, значит, ни одно из этих
левая часть уравнения отрицательна, а первая – неотрицательна, значит, ни одно из этих ![]() решением уравнения быть не может.
решением уравнения быть не может.
Пусть ![]() . Для таких
. Для таких ![]() обе части уравнения неотрицательны, и поэтому оно равносильно на этом множестве уравнению:
обе части уравнения неотрицательны, и поэтому оно равносильно на этом множестве уравнению: ![]() .
.
Введем новую переменную. ![]() . Получаем, что
. Получаем, что ![]() . Тогда
. Тогда ![]() - не удовлетворяет условию
- не удовлетворяет условию ![]() ,
, ![]() .
.
Выполним обратную замену.
![]() ;
; ![]() ;
; ![]()
![]() .
.
Тогда ![]() - не удовлетворяет условию
- не удовлетворяет условию ![]() ,
,
![]()
О т в е т: ![]() .
.
Пример 7. Решить уравнение ![]()
Решение. Найдем ОДЗ переменной х.
ОДЗ: 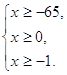
Следовательно, что ![]()
Легко видеть, что ![]() , т.к.
, т.к. ![]() .
.
Разделим обе части уравнения на ![]() . Получаем, что
. Получаем, что
![]()
Преобразуем ![]() . Введем новую переменную. Пусть
. Введем новую переменную. Пусть ![]() , а
, а ![]() . Тогда уравнение примет вид:
. Тогда уравнение примет вид: ![]() ;
; ![]() ;
; ![]() :
: ![]() . Тогда
. Тогда ![]() - не удовлетворяет условию
- не удовлетворяет условию ![]() ,
, ![]() . Выполним обратную замену.
. Выполним обратную замену.
![]()
О т в е т: ![]() .
.
Пример 8. Решить уравнение ![]()
Решение. Преобразуем исходное уравнение.![]()
![]()
Возведем обе части полученного уравнения в квадрат.

Тогда ![]()
Итак, проверка показывает, что -1,2 - не является корнем исходного уравнения, а 3 - является.
Замечание. Данное уравнение можно решать и с помощью равносильных переходов, но тогда его решении будет намного сложнее, чем приведенное выше.
О т в е т: {3}.
Пример 9. Решить уравнение ![]()
Решение. Заметим, что все квадратные трехчлены положительны относительно ![]()
![]() . Перепишем уравнение в виде:
. Перепишем уравнение в виде:
![]()
Обозначим для краткости подкоренные выражения через ![]() соответственно. Умножим и разделим левую и правую часть уравнения на сопряженные сомножители. Получаем, что
соответственно. Умножим и разделим левую и правую часть уравнения на сопряженные сомножители. Получаем, что

Вернемся к уравнению.

Второе уравнение совокупности решений не имеет, поскольку оба знаменателя положительны. Следовательно, ![]()
Замечание. Также решение данного уравнения можно найти, исследуя его на разных числовых промежутках.
Сначала выделим ![]() и
и ![]() соответственно в каждом из подкоренных выражений в правой части уравнения.
соответственно в каждом из подкоренных выражений в правой части уравнения.

Следовательно, исходное уравнение имеет вид:
![]()
Обозначим для краткости подкоренные выражения через ![]() ,
, ![]() ,
, ![]() и
и ![]() соответственно. Т.к. выражение
соответственно. Т.к. выражение ![]() обращается в ноль при
обращается в ноль при ![]() , то рассмотрим решение данного уравнения при
, то рассмотрим решение данного уравнения при ![]() ,
, ![]() и
и ![]() .
.
Если ![]() , то
, то ![]() >
>![]() ,
, ![]() >
>![]()
![]()
![]() +
+![]() >
>![]() +
+![]() .
.
Следовательно, при ![]() исходное уравнение не имеет корней.
исходное уравнение не имеет корней.
Если ![]() , то
, то ![]() <
<![]() ,
, ![]() <
<![]()
![]()
![]() +
+![]() <
<![]() +
+![]() .
.
Следовательно, при ![]() исходное уравнение не имеет корней.
исходное уравнение не имеет корней.
Если ![]() , то
, то ![]() =
=![]() ,
, ![]() =
=![]()
![]()
![]() +
+![]() =
=![]() +
+![]() .
.
Следовательно, -1 является единственным корнем исходного уравнения.
О т в е т:{-1}.
Замечание. Следовательно, при решении уравнений с радикалами надо уметь пользоваться любым из этих методов и выбирать в каждом случае оптимальный.
3. Не стандартные методы решения иррациональных уравнений
Существуют иррациональные уравнения, которые считаются для школьников обычных образовательных школ задачами повышенной трудности. Для решения таких уравнений лучше применять не традиционные методы, а приемы, которые не совсем привычны для учащихся. В этой главе приводятся решения уравнений основанных на графических соображений, свойствах функции (таких, как монотонность, ограниченность, четность), применении производной и т.д.
Похожие работы
... введение нового(новых) неизвестного. Пример 2. Обозначим , тогда а) Уравнение примет вид: Корень не удовлетворяет условию Ответ: 76. Методы решения иррациональных уравнений. Методы решения иррациональных уравнений, как правило основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному, либо ...
... , т.к. . б) , т.к. . в) . Выясним, при каких n выражения под знаком модуля меняют знак: n=-1, n=1, n=0. 1) Если n<-1, то 2) Если -1£n<0, то 3) Если 0<n<1, то 4) Если n³1, то Ответ: II. Иррациональные уравнения. Рассмотрим уравнение вида . Основной метод решения – возведение обеих частей уравнения в степень n. При этом, если n – четное, то могут возникнуть ...
... по способам решения иррациональных неравенств вида , рассмотрена подробно, изложение теории строгое. Только в учебнике Виленкина рассматривается решение иррационального неравенства вида . Наиболее большой объем упражнений для решения иррациональных уравнений и неравенств представлен в учебниках [11] и [5]. В учебнике [4] упражнений не много, но они разнообразны. Основные понятия, относящиеся к ...
... литературы дается характеристика этих форм, разработана методика применения самостоятельной работы вместе с иными формами организации познавательной деятельности на факультативных занятиях в выпускных классах средней школы, изучены учебные возможности учащихся в экспериментальной группе, проведена опытно- экспериментальная работа по включению самостоятельной работы школьников в процесс обучения. ...


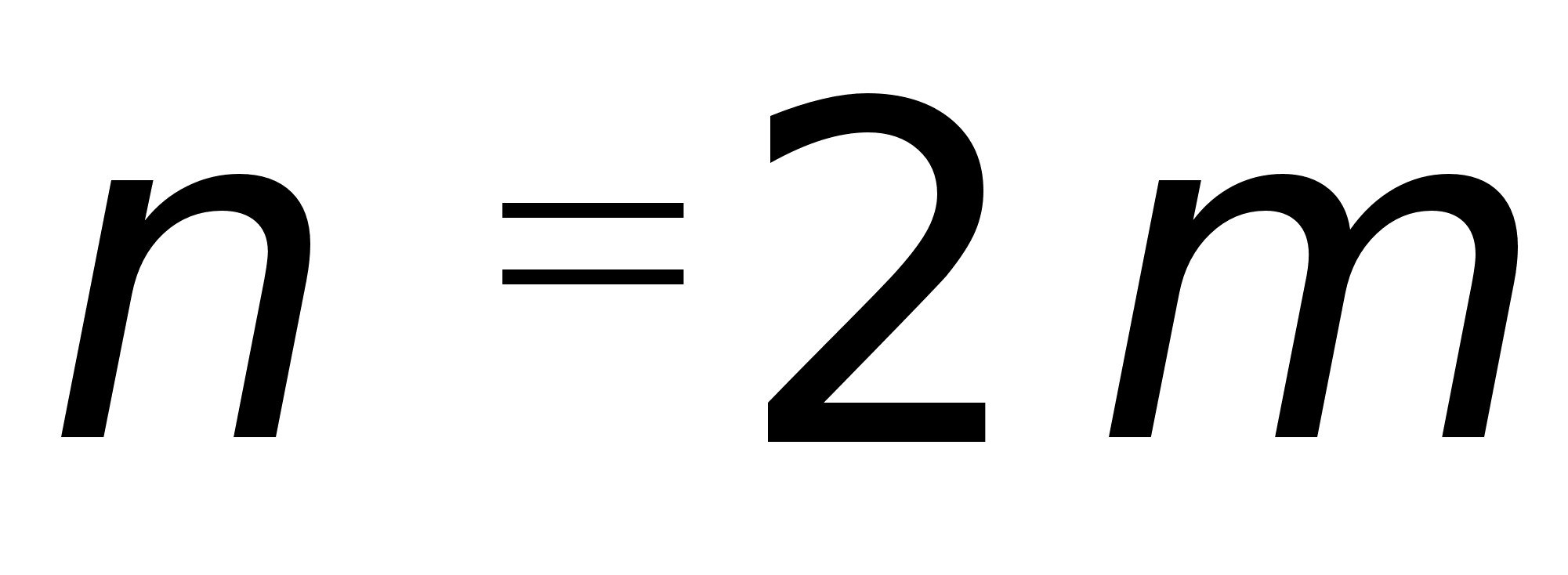
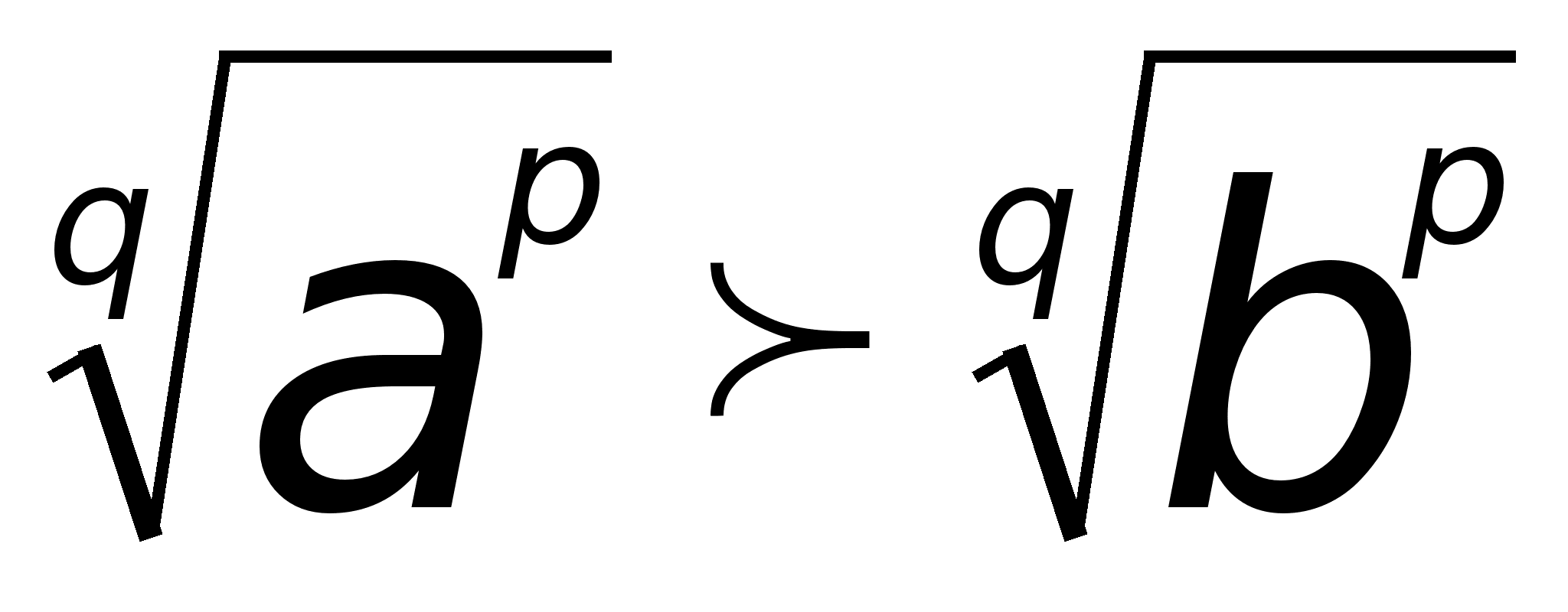
0 комментариев