Навигация
Решить линейное уравнение 1-го порядка
2. Решить линейное уравнение 1-го порядка
![]()
Ищем решение уравнения в виде произведения двух функций: ![]()
При этом:
![]()
После подстановки в исходное уравнение имеем:
![]()

Чтобы коэффициент при u обратился в 0, в качестве v выбираем функцию удовлетворяющую уравнению:

Найдем функцию u, которая должна удовлетворять уравнению:
 :
:
Решение запишется в виде:
![]()
3 ![]()
Это неоднородное линейное дифференциальное уравнение второго порядка. Его решение ищем в виде:
![]() , где
, где ![]() - общее решение соответствующего однородного уравнения,
- общее решение соответствующего однородного уравнения, ![]() - частное решение.
- частное решение.
Найдем ![]()
Решим однородное дифференциальное уравнение
![]()
Характеристическое уравнение для него:
![]()
Это квадратное уравнение
d=36-100=-64 – дискриминант отрицательный, корни комплексные:
k1=3-4i ; k2=3+4i
Общее решение, следовательно, имеет вид:
![]() ,
,
где ![]() - константы.
- константы.
Ищем частное решение. Функция свободного члена имеет вид:
![]() , где a=2,b=3,k=1,p=-6,q=25
, где a=2,b=3,k=1,p=-6,q=25
При этом ![]() , следовательно, частное решение ищем в виде:
, следовательно, частное решение ищем в виде:
![]()
Находим его производные первого и второго порядка и подставляем в уравнение:

Для нахождения коэффициентов А и В решим систему:

A=0,07, B=0,16
Таким образом, окончательное решение уравнения имеет вид:
![]()
IV. Ряды
1. Исследовать на сходимость ряд с положительными членами
![]()
Рассмотрим ряд:
![]()
Это степенной ряд с основанием меньшим 1, а он заведомо сходится.
Теперь сравним члены ряда ![]() с членами ряда
с членами ряда ![]()
![]() при n>4 , значит ряд
при n>4 , значит ряд ![]() также сходится.
также сходится.
2. Исследовать на абсолютную и условную сходимость ряд:
![]()
Исследуем на абсолютную сходимость (сходимость ряда, состоящего из модулей членов знакопеременного ряда) значит необходимый признак сходимости выполняется.
![]() ,
,
Сравним член этого ряда с членом заведомо расходящегося гармонического ряда:
![]() , следовательно наш ряд расходится абсолютно.
, следовательно наш ряд расходится абсолютно.
Исследуем ряд на условную сходимость:
Так как условия признака Лейбница выполнены
![]()
данный ряд сходится условно.
3. Найти область сходимости функционального ряда
![]() , перепишем его в виде:
, перепишем его в виде:
![]()
Член данного ряда представляет собой член степенного ряда, помноженный на член гармонического ряда.
Для расходящегося гармонического ряда выполняется однако основной признак сходимости (его член стремится к нулю), так что сходимость функционального ряда ![]() определяется сходимостью степенного ряда:
определяется сходимостью степенного ряда: ![]() , причем при любом x это будет знакопостоянный ряд.
, причем при любом x это будет знакопостоянный ряд.
Cтепенной же ряд сходится когда его член по модулю <1:
![]()
Решаем это модульное неравенство и находим область сходимости функционального ряда ![]() :
:
![]()

Итак, область сходимости функционального ряда ![]() :
:
![]()
Похожие работы
... , которые содержат неизвестную функцию, её производные и аргументы. Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Если неизвестная функция является функцией многих переменных, то соответствующее уравнение называется дифференциальным уравнением в частных производных. Порядком дифференциального уравнения называется наивысший ...
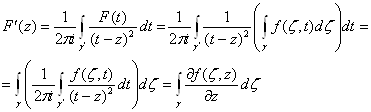
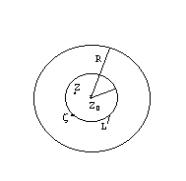
... зависимость от параметра. Рассматривая интеграл Коши, мы видим, что подынтегральная функция зависит от двух комплексных переменных: переменной интегрирования и фиксированного значения переменной . Тем самым интеграл Коши является интегралом, зависящим от параметра. Естественно поставить вопрос об общих свойствах интегралов по комплексной переменной, зависящих от параметра. Пусть задана функция ...
... переменных Z и z при произвольном изменении области G и переменных на кривой С. Очевидно, что при сделанных предположениях : Интеграл существует и является функцией комплексной переменной. Справедлива формула : (2) Эта формула устанавливает возможность вычисления производной от исходного интеграла путем дифференцирования подинтегральной функции по параметру. ТЕОРЕМА. Пусть f(Z) ...
... его тождество. Общим решением дифференциального уравнения го порядка называется такое его решение , которое является функцией переменных и произвольных независимых постоянных . Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных . Теорема. Пусть в дифференциальном уравнении (1) функция ...
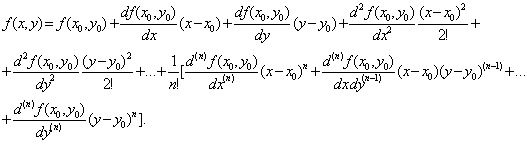

0 комментариев