Навигация
Приведення до канонічної форми
3. Приведення до канонічної форми
Покажемо, нарешті, що кожен інтеграл типу (7) може бути представленим у формі
 (8)
(8)
де k – деякий додатній правильний дріб: 0<k<1. Назвемо цю форму канонічною.
Введемо скорочено
![]()
Не зменшуючи загальності, дозволяється вважати тут А = ± 1; крім того, для визначеності обмежимося додатніми значеннями t. Розглянемо тепер різні можливі комбінації знаків A, m, m’ і вкажемо для кожного випадку підстановку, що безпосередньо приводить інтеграл (7) в канонічну форму.
1) А = +1, ![]()
![]() (
(![]() ). Для того, щоб радикал мав дійсні значення, необхідно, щоб було
). Для того, щоб радикал мав дійсні значення, необхідно, щоб було  або
або  Припускаємо, що
Припускаємо, що
![]() де 0<z<1 або
де 0<z<1 або 
Тоді
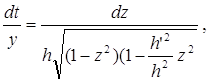
так, що за k тут треба прийняти ![]()
2) А = +1, ![]()
![]() (h, h’>0). Для того, щоб радикал мав дійсні значення, обмежимося значеннями
(h, h’>0). Для того, щоб радикал мав дійсні значення, обмежимося значеннями  .
.
Припускаємо, що
![]() де 0 < z ≤ 1.
де 0 < z ≤ 1.
Тоді
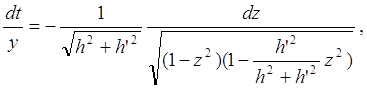
і можна взяти 
3) А = +1, ![]()
![]() (h>h’>0). Зміна t нічим не обмежена. Припустимо
(h>h’>0). Зміна t нічим не обмежена. Припустимо
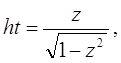 де 0≤z<1.
де 0≤z<1.
В цьому випадку

і ![]()
4) А = -1, ![]()
![]() (h, h’>0). Зміна t обмежена нерівністю
(h, h’>0). Зміна t обмежена нерівністю ![]() . Беремо
. Беремо
 , де 0<z<1 ,
, де 0<z<1 ,
так, що
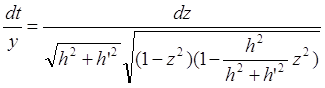
і ![]() .
.
5) А = -1, ![]()
![]() (h>h’>0). Змінна t може змінюватися лише між
(h>h’>0). Змінна t може змінюватися лише між ![]() і
і ![]() . Припустимо
. Припустимо
 , де 0<z<1.
, де 0<z<1.
Маємо
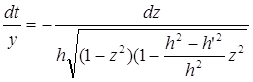
і  Цим вичерпуються всі можливі випадки, тому що у випадку, коли А = -1 і обидва числа m, m’ > 0, радикал взагалі не міг би мати дійсних значень. Про множник
Цим вичерпуються всі можливі випадки, тому що у випадку, коли А = -1 і обидва числа m, m’ > 0, радикал взагалі не міг би мати дійсних значень. Про множник ![]() ми не говорили нічого, тому що у всіх випадках він, очевидно, перетворювався у раціональну функцію від
ми не говорили нічого, тому що у всіх випадках він, очевидно, перетворювався у раціональну функцію від ![]() .
.
Відмітимо ще, що розглядаючи інтеграл (8), ми можемо обмежуватися значеннями z<1; випадок ![]() приводиться до цього підстановкою
приводиться до цього підстановкою ![]() , де
, де ![]() <1.
<1.
Похожие работы
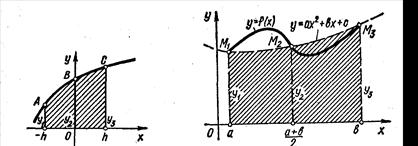
... . Тоді, якщо існує скінченна границя (13), її називають невласним інтегралом першого роду і позначають так: (14) Таким чином, за означенням (15) У цьому випадку інтеграл (14) називають збіжним, а підінтегральну функцію f(x) – інтегрованою на проміжку (а;+). Якщо ж границя (13) не існує або нескінченна, то інтеграл (14) називають також невласним але розбіжним, а функція f(x) – ...
... на малому , g(x,y) стала y1 = y(x0 ) + y(x0 ) + g(x0, y0 ) x Повторюючи знайдемо y2 = y(x1+x) y(x1) + g(x1, y1 ) x yn= yn-1+ g(xn-1 ,yn-1) x, (n=0,1,2…) нахил дотичної визначається початковою точкою інтервалу. 2.3. Програма для комп’ютера. Алгоритм методу. 1. Вибирається початкова умова, величина кроку і кількість ітерацій (кроків). 2. Визначається y і нахил у початковій точці ...
... метод координат. V. Аксіома паралельності Сама остання аксіома грає в геометрії особливу роль, визначаючи поділ геометрії на дві логічно несуперечливі й взаємно виключають один одного системи: Евклідову й неевклідову геометрії. У геометрії Евкліда ця аксіома формулюється так. V. Нехай а – довільна пряма й А – крапка, що лежить поза прямій а, тоді в площині α, обумовленою крапкою А и ...
... для систем, частинок з антисиметричними хвильовими функціями, тобто до ферміонів. 2.2.3. Розподіл електронів за станами. Періодична система елементів. Сукупність електронів, які перебувають у всіх можливих станах з однаковим значенням головного квантового числа n, утворює електронну оболонку (електронний шар). Енергетичні шари прийнято позначати великими латинськими літерами відповідно до ...


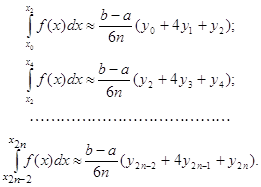
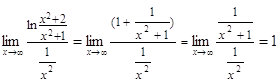




0 комментариев