Навигация
Рассчитаем и построим ЛАЧХ и ЛФЧХ скорректированной разомкнутой системы
1.4.1 Рассчитаем и построим ЛАЧХ и ЛФЧХ скорректированной разомкнутой системы
Используем передаточную функцию разомкнутой системы (1.10)
![]()
Для получения частотной передаточной функции заменим S на jw и преобразуем

![]()
Вещественная и мнимая части соответственно:
![]() (1.11)
(1.11) ![]() ; (1.12)
; (1.12)
Тогда

![]() .
.
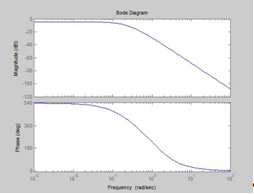
ЛАЧХ и ЛФЧХ разомкнутой системы представлены ниже.
ЛАЧХ скорректированной системы сместилась вправо, следовательно, необходимые требования по точности выполняются, запасы устойчивости увеличились по сравнению с системой с пропорциональным регулятором.

–– ЛАЧХ и ЛФЧХ скорректированной системы
- - ЛАЧХ и ЛФЧХ системы с пропорциональным регулятором
Рисунок 1.15 ЛАЧХ и ЛФЧХ систем
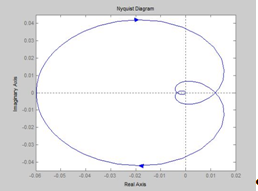
Построим график АФЧХ по имеющимся формулам (1.11) и (1.12) и сравним его с графиком системы с пропорциональным регулятором. Он представляет собой годограф Найквиста, поэтому сделаем ниже дополнительно выводы об устойчивости системы.
Составим таблицу, изменяя w от 0 до ∞:
Таблица 1.3
| W, | P(w) | Q(w) |
| 0 | -10,604 | -∞ |
| 852,2 | 0 | 5,806*10-3 |
| 274,2 | -0,094 | 0 |
|
| 0 | 0 |
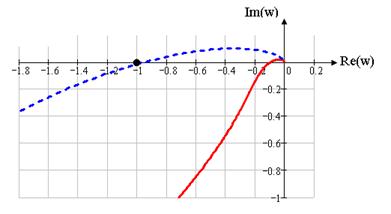
–– годограф скорректированной системы
- - годограф системы с пропорциональным регулятором
Рисунок 1.16 – Годограф Найквиста
Характеристическое уравнение имеет вид:
![]()
Все корни характеристического уравнения, кроме одного нулевого, левые, следовательно, разомкнутая система на границе устойчивости. Для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф Найквиста, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывал особу точку (-1; j0). Данное условие выполняется, значит, замкнутая система устойчива.
Построим годограф Михайлова для системы.
Передаточная функция замкнутой системы:
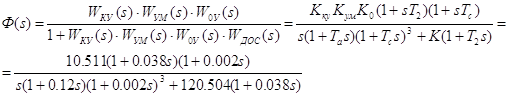 (1.13)
(1.13)
Функция Михайлова имеет вид:
![]() (1.14)
(1.14)
Выполним замену S на jw и выделим вещественную и мнимую части соответственно.
![]() .
.
![]() ;
;
Найдем значения X(w) и Y(w), изменяя при этом w от 0 до ∞:
Таблица 1.4
| w, | X(w) | Y(w) |
| 0 | 85.227 | 0 |
| 26.125 | 0 | 114.613 |
| 79.717 | -648.966 | 0 |
| 275.355 | 0 | -13120 |
| 816.259 | 6.473*106 | 0 |
|
|
|
|
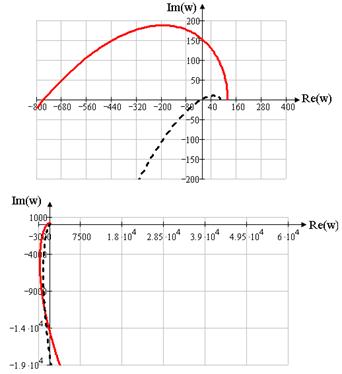
–– скорректированной системы
- - системы с пропорциональным регулятором
Рисунок 1.17 годограф Михайлова для замкнутой системы
Годограф Михайлова начинается на вещественной положительной оси и при изменении частоты w от 0 до +![]() последовательно проходит 5 квадрантов против часовой стрелки, нигде не обращаясь в ноль. Это свидетельствует об устойчивости замкнутой системы.
последовательно проходит 5 квадрантов против часовой стрелки, нигде не обращаясь в ноль. Это свидетельствует об устойчивости замкнутой системы.
Рассчитаем и построим для замкнутой системы АЧХ “вход- выход системы”. Для этого воспользуемся передаточной функцией замкнутой системы (1.13). Заменим s на jw и преобразуем данное выражение:
![]()
![]()
![]()
Выделим вещественную и мнимую части соответственно:
![]()
![]()
Находим
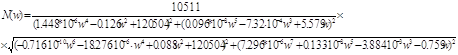 (1.15)
(1.15)
График АЧХ “вход- выход системы” представлен ниже.
Рассчитаем и построим АЧХ “вход- выход ДОС”. Запишем передаточную функцию замкнутой системы по выходу ДОС, которая имеет вид:
![]()
Преобразуем данное выражение:
![]()
![]()
![]()
Вещественная и мнимая части соответственно:
![]() (1.16)
(1.16)
![]()
Получим модуль передаточной функции замкнутой системы по выходу ДОС:
![]()
![]()
(1.17)

––– АЧХ «вход- выход ДОС»,
- - - АЧХ «вход- выход системы».
Рисунок 1.18 АЧХ
Рассчитаем и построим АЧХ “вход- выход УМ ”. Передаточная функция замкнутой системы по выходу УМ имеет вид:
![]()
![]() (1.18)
(1.18)
Вещественная и мнимая части соответственно:
![]()
![]()
Модуль передаточной функции замкнутой системы по выходу УМ:
![]()
![]()
![]()

Рисунок 1.19 АЧХ вход-выход УМ
1.4.3 Частота среза разомкнутой системы, запасы устойчивости, критический коэффициент усиления, показатель колебательностиЧастота среза и запасы устойчивости разомкнутой системы определяются по ЛАЧХ и ЛФЧХ. Определим их из рисунка 1.15
ЛАЧХ пересекает ось в точке lg(w)=1.614 дек. Тогда wср=41.072 с-1
ЛФЧХ пересекает уровень -180° при lg(w)=2.438 дек. Тогда wкр=274.35 с-1
Запас устойчивости по амплитуде найдем по годографу Найквиста:
![]()
Где hзап- расстояние до точки пересечения годографа Найквиста с действительной осью. (рис. 1.16)
![]() дБ
дБ
Запас устойчивости по фазе определим по рисунку 1.15:
φзап=φ(wcp)+1800
φзап=54,7330
Критический коэффициент найдем с использованием критерия Гурвица:
Характеристическое уравнение замкнутой системы имеет вид:
![]() (3.1)
(3.1)
Тогда оставим переменным параметр: K.
Получим следующие коэффициенты:
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения системы на границе устойчивости должны выполняться следующие условия:
1) одинаковость знака всех коэффициентов
2) для системы 5 порядка определитель D4=0
Решая уравнение в пакете MathCad получим следующие результаты:
![]()
Показатель колебательности определим по формуле:
![]() ,
,
![]() и N(0) находим по АЧХ замкнутой системы по выходу ДОС
и N(0) находим по АЧХ замкнутой системы по выходу ДОС
N(0)=1
Nmax=1.239,
Следовательно![]() .
.
Сравним результаты с результатами, полученными в пункте 1.2.3
Таблица 1.5 – Сравнительная характеристика полученных результатов
| Lзап, дБ |
| Ккр | М |
| tp, с | |
| С регулятором | 0,409 | 0,75 | 93,3 | 75,214 | 95 | 22,72 |
| С коррекцией | 10,6 | 54,733 | 431 | 1.239 | 18,8 | 0,147 |
Оценим σ и tp по вещественной частотной характеристике системы.
Построим вещественную частотную характеристику (ВЧХ) “вход – выход ДОС”. Для этого используем выражение (1.16).
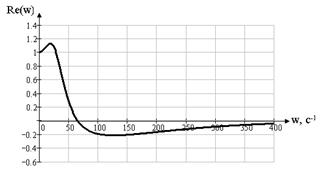
Рисунок 1.20 ВЧХ вход – выход ДОС
Склонность системы к колебаниям тем больше, чем выше пик у вещественной характеристики.
Оценим σ по формуле:
![]() ,
,
где ![]() максимальное значение ВЧХ;
максимальное значение ВЧХ;
![]() минимальное значение ВЧХ;
минимальное значение ВЧХ;
P(0)- значение ВЧХ при w=0.

Подставляем значения и находим: ![]() .
.
tp оценим по формуле: ![]()
С помощью трассировки определили wn= 65,5 c-1.
Следовательно tp>0.048c-1.
ЛЧХ “вход- выход ДОС”
Для построения найдем L(w), используя выражение (1.15):
![]()
ЛФЧХ “вход- выход ДОС” построим по формуле
![]() Подставляя ранее полученные выражения Q(w) и P(w) (1.16), получим
Подставляя ранее полученные выражения Q(w) и P(w) (1.16), получим
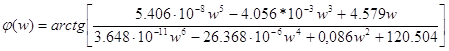
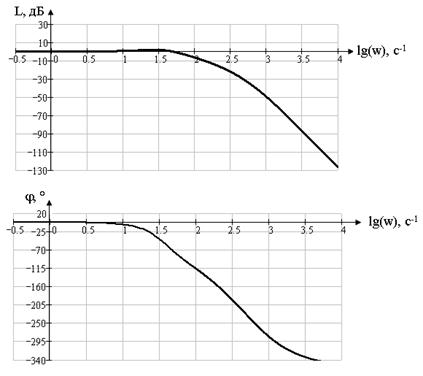
Рисунок 1.21 ЛАЧХ и ЛФЧХ вход- выход ДОС
Найдем нули и полюса замкнутой системы “вход- выход ДОС” и изобразим их на комплексной плоскости.
Корни полинома числителя называют нулями передаточной функции, а корни полинома знаменателя – полюсами.
![]()
Найдем их с помощью пакета MathCad [приложение 1].
Таблица 1.6– Нули и полюса замкнутой системы «вход- выход ДОС»
| нули | -26.316 | -500 | |||
| полюса | -610.77+159.74j | -610.77-159.74j | -234.44 | -26.175,89-j25.657 | -26.175+j25.657 |
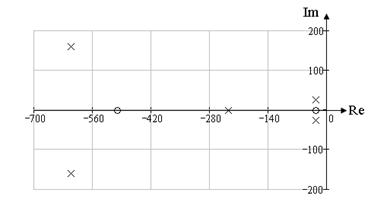
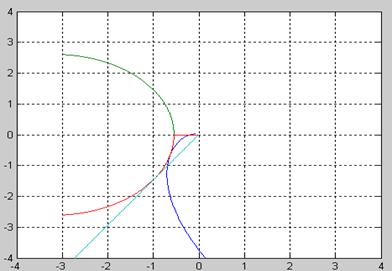
Рисунок 1.22 Нули и полюса на комплексной плоскости
Вычислим корневые оценки прямых показателей качества [1.§ 8.6].
Степень устойчивости η – это расстояние от мнимой оси до наиболее близко расположенного к ней полюса.
Ближайшим к мнимой оси является вещественный полюс, значит η – апериодическая степень устойчивости. ![]() .
.
Ближайшие к мнимой оси полюса называются доминирующими.
Доминирующие полюса дают составляющей переходного процесса затухание наиболее медленно. Поэтому по η можно получить оценку времени регулирования:
![]()
Колебательность ![]() ,
,
где β– мнимая часть, α– вещественная часть доминирующих комплексно-сопряженных полюсов.
Доминирующие комплексно-сопряженные полюса: -26.175± j25,657.
![]()
Удаленные от начала координат полюса увеличивают перерегулирование
![]() Получаем
Получаем ![]()
Определим влияние нулей на оценки прямых показателей качества.
Близко расположенные нуль и полюс взаимно компенсируются. Скомпенсированный нулем полюс не участвует в оценке прямых показателей качества.
![]() ,
,
где λi – вещественная часть полюса;
nj- вещественная часть нуля.
В данной работе близко расположенные нули и полюса отсутствуют.
Оценка точности системыТочность СУ оценивается в статическом режиме – в режиме, соответствующем окончанию переходного процесса (t→¥).
Анализ точности начинается с передаточной функции замкнутой системы по ошибке ФЕ(s). [1, § 8.3]
Эту передаточную функцию разлагаем в ряд:
![]()
Где сi – коэффициенты ошибки.
Найдем выражения для вычисления первых двух коэффициентов ошибки и занесем в табличку.
Таблица 1.7
| С0 | С1 | |
| выражение для ошибки | 0 |
|
| Значение ошибки | 0 | 0.008 |
Рассчитаем установившуюся ошибку системы для заданных в ТЗ сигналов.
![]()
Тогда для входного сигнала ![]() получаем установившуюся ошибку:
получаем установившуюся ошибку: ![]()
Для входного сигнала ![]() с постоянной скоростью, где А=6В/с, установившаяся ошибка:
с постоянной скоростью, где А=6В/с, установившаяся ошибка:
![]() В
В
Установившуюся ошибку для гармонического сигнала вида ![]() рассчитаем по следующей формуле:
рассчитаем по следующей формуле:
![]() , (1.19)
, (1.19)
где ![]() - заданная частота,
- заданная частота,
![]() -модуль частотной передаточной функции по ошибке,
-модуль частотной передаточной функции по ошибке,
А0=1В- амплитуда входного сигнала,
![]() - аргумент частотной передаточной функции по ошибке.
- аргумент частотной передаточной функции по ошибке.
![]() .
.
Поскольку частота выходного сигнала (ошибки) совпадает с частотой входного сигнала, найдем NEи φE на частоте ![]() .
.
Определим частоту гармонического входного сигнала ![]() , для которой амплитуда установившихся колебаний на выходе усилителя мощности равна 110В при амплитуде входного сигнала 1В.
, для которой амплитуда установившихся колебаний на выходе усилителя мощности равна 110В при амплитуде входного сигнала 1В.
![]() определим по графику АЧХ “вход-выход УМ” (Рис. 1.19). Получаем, что w0=11,215.
определим по графику АЧХ “вход-выход УМ” (Рис. 1.19). Получаем, что w0=11,215.
Найдем NE частотной передаточной функции по ошибке. Выделим вещественные и мнимые части:
![]()
![]()
![]()
Модуль частотной передаточной функции по ошибке:
![]()
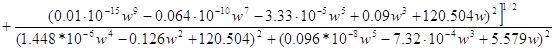
N(w0)=0.1
Определим аргумент частотной передаточной функции по ошибке:
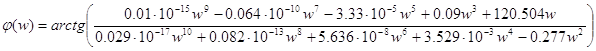 ;
; ![]() .
.
Подставляя найденные значения в формулу (1.19) получим установившуюся ошибку при гармоническом входном сигнале:
![]()
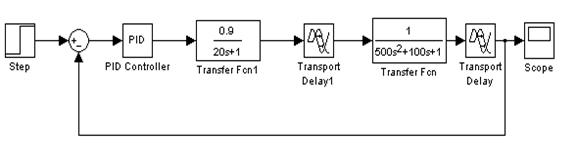
2. Отработка типовых входных сигналов 2.1 Единичная ступенька 2.1.1 Переходная функция по выходу системы
Известно несколько способов расчета реакции системы на входные сигналы. В данной работе используем метод преобразований по Лапласу.
Запишем переходную функцию системы по выходу системы при входном воздействии X(t) = 1(t)
![]() – изображение по Лапласу входного единичного сигнала.
– изображение по Лапласу входного единичного сигнала.
Переходная функция h(t) определяется по формуле:
![]() (2.1)
(2.1)
Найдем переходную функцию по выходу системы:
 ; (2.2)
; (2.2)
Начальные и конечные значения переходной функции находятся по формулам:
![]() (2.3)
(2.3)
![]()
Начальное и конечное значение переходной функции по выходу системы:
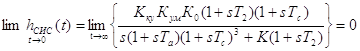 (2.4)
(2.4)
 (2.5)
(2.5)
Т.е. конечное значение переходной характеристики системы по выходу системы зависит только от коэффициентов усиления звеньев.
Найдем переходную функцию по выходу ДОС:
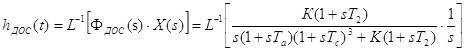 ; (2.6)
; (2.6)
По формулам (2.3) найдем начальное и конечное значение переходной функции по выходу ДОС:
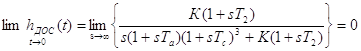 (2.7)
(2.7)
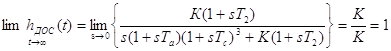 (2.8)
(2.8)
Т.е. переходная характеристика системы по выходу ДОС не зависит от параметров системы.
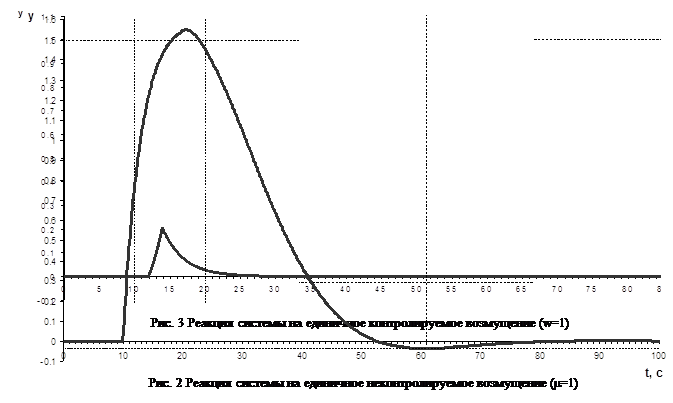
Реакция системы представлена на Рисунке 1.14 (п. 1.3.5).
Найдем переходную функцию по выходу УМ [приложение 2]:
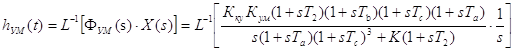 ; (2.9)
; (2.9)
По формулам (2.3) найдем начальное и конечное значение переходной функции по выходу системы:
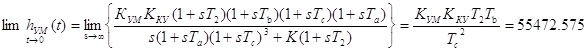 (2.10)
(2.10)
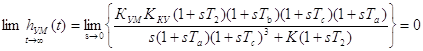 (2.11)
(2.11)
Т.е. начальное значение переходной характеристики системы по выходу УМ зависит не только от коэффициентов УМ и КУ системы, а также от частот сопряжений w2 и wb.
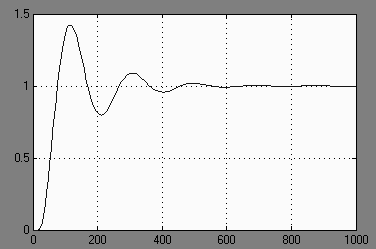
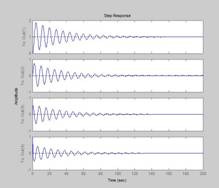
2.1.2 Переходные характеристики системы По формуле (2.2) построим переходный процесс по выходу системы.
Рисунок 2.1 Переходная характеристика по выходу системы
hmax=0.105, hуст=0,087, тогда
![]() ,
,
Определим время переходного процесса tpпостроив “коридор”, равный ![]() , из Рисунка 2.1 определяем, что tp=0.151с
, из Рисунка 2.1 определяем, что tp=0.151с
Перерегулирование и время переходного процесса по выходу ДОС соответственно:
![]() , tp=0.147 с.
, tp=0.147 с.
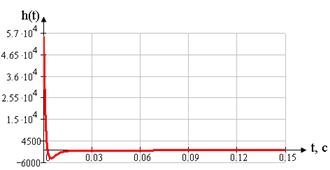
Рисунок 2.4 Переходная характеристика системы по выходу УМ
2.1.3 Сравнение переходных характеристикОпределенные по переходным характеристикам прямые показатели качества, для сравнения представим в табл. 2.2 вместе с оценками, полученными в пункте 1.4.4.
Таблица 2.2
| по выходу системы | по выходу ДОС | Оценки по ВЧХ | Корневые оценки | |
| s,% | 19,5 | 18,8 | 26,704 | 4,053 |
| tP, с | 0,151 | 0,147 | 0.048 | 0,146 |
По данным таблицы можно сделать вывод, что постоянная времени датчика обратной связи незначительно влияет на качество переходного процесса.
Показатели качества, полученные по переходным характеристикам, по ВЧХ и корневым оценкам, отличаются. Это объясняется тем, что получаем оценку, а не само значение.
Запишем все значения в таблицу для наглядности.
Таблица 2.3
| графически | аналитически | ||
| вход–выход системы | h(0) | 0 | 0 |
| h(∞) | 0,087 | 0,087 | |
| вход–выход ДОС | h(0) | 0 | 0 |
| h(∞) | 1 | 1 | |
| вход-выход УМ | h(0) | 55472,575 | 55472,575 |
| (∞) | 0 | 0 |
Сравнивая начальные и конечные значения переходных характеристик по всем выходам, определенные аналитически по передаточным функциям в пункте 2.1.1, с их расчетными значениями, мы видим, что они совпадают.
2.1.4 Величина ступенчатого сигналаОпределим величину Х0 ступенчатого сигнала, при котором система работает в зоне линейности усилителя мощности. Допустимая величина входного сигнала ограничена напряжением насыщения усилителя мощности, равным 110 В. Наибольшее значение выхода УМ достигается при t = 0. Допустимую величину "ступеньки" Х0 определим из пропорции:
![]() ;
;
Подставляя значения, получаем![]() .
.
Величина Х0 = 0,002В.
2.2 Сигнал с постоянной скоростью
Рассчитаем и построим график ошибки системы при отработке входного сигнала с постоянной скоростью, вида:
X(t) = А×t, где А=6 В/с.
Изображение по Лапласу сигнала: ![]() ,
,
Переходная функция по ошибке примет вид:
![]()
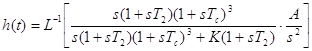 ;
;

––– график ошибки при отработке входного сигнала с
постоянной скоростью;
![]() график вынужденной (установившейся) составляющей ошибки
график вынужденной (установившейся) составляющей ошибки
при отработке входного сигнала с постоянной скоростью.
Рисунок 2.5
Интервал времени, на котором практически (с точностью 5%) устанавливается вынужденный режим определим по рисунку 2.5.
Таким образом, tв=0.13 с.
Время, за которое практически устанавливается вынужденный режим, tв=0.13с меньше, чем время регулирования tp=0.147c.
2.3 Гармонический сигнал 2.3.4 Определение частоты гармонического сигнала
Определим частоту гармонического сигнала по АЧХ замкнутой системы по выходу УМ (п. 1.4.2).
Из Рис. 1.19 следует, что значение частоты![]() 0 =11.823-1.
0 =11.823-1.
Таким образом, частота гармонического входного сигнала, при которой амплитуда установившихся колебаний на выходе УМ равна 110В, при амплитуде входного 1В, равна 11.823-1.
2.3.2 График реакции системы по выходу ДОС при подаче гармонического сигнала на вход системыВходной сигнал и его изображение по Лапласу имеют вид:
X(t) = sin(w0×t), (2.11)
![]() .
.
Реакцию системы на гармонический входной сигнал по выходу ДОС определим по формуле:
![]()

На Рисунке 2.6 представлен график реакции на входное гармоническое воздействие по выходу ДОС.
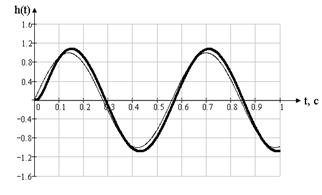
![]() реакция по выходу ДОС
реакция по выходу ДОС
––––– входное гармоническое воздействие
Рисунок 2.6
2.3.3 Амплитудно-фазовые искажения отработки входного сигналаАмплитудные искажения отработки входного сигнала определим по формуле:

где ![]() – максимальное значение амплитуды выходного сигнала;
– максимальное значение амплитуды выходного сигнала;
![]() – максимальное значение амплитуды входного сигнала;
– максимальное значение амплитуды входного сигнала;
![]() и
и ![]() определим по графику вынужденной составляющей сигнала по выходу ДОС (Рис. 2.6)
определим по графику вынужденной составляющей сигнала по выходу ДОС (Рис. 2.6)
![]() =1,083,
=1,083, ![]() =1
=1
Подставляя значения, получаем: 
Определим амплитудные искажения по ЛАЧХ разомкнутой системы на частоте w0.
По Рис. 1.21 на частоте w0=11,823с-1![]()
Фазовые искажения отработки входного сигнала определяются по формуле:
![]() .
.
где t = 0.011 с - временной сдвиг между входным сигналом и сигналом ДОС, определено по Рис. 2.6. и ![]() – по ЛФЧХ (рис 1.21) отличаются незначительно, что можно объяснить округлениями при вычислении.
– по ЛФЧХ (рис 1.21) отличаются незначительно, что можно объяснить округлениями при вычислении.
3. Область устойчивости
Рассчитаем и построим границу области устойчивости на плоскости параметров «постоянная времени корректирующего устройства Тa–коэффициент усиления разомкнутой системы К».
Построим область устойчивости c помощью критерия Гурвица.
Характеристическое уравнение замкнутой системы имеет вид:
 (3.1)
(3.1)
Тогда оставим переменными 2 параметра: K и Т2.
Получим следующие коэффициенты:
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения системы на границе устойчивости должны выполняться следующие условия:
3) одинаковость знака всех коэффициентов
4) для системы 5 порядка определитель D4=0
Решая уравнение в пакете MathCad, [приложение 3]получим следующий график:

Рисунок 3.1 Область устойчивости
Точка Kкр, найденная в пункте 1.4.3 практически совпадает с точкой, полученной по графику. Значение коэффициента, соответствующее расчетным параметрам находится в зоне области устойчивости. Т.е. при данных параметрах система устойчива. Небольшая погрешность в расчетах возникает из-за округлений.
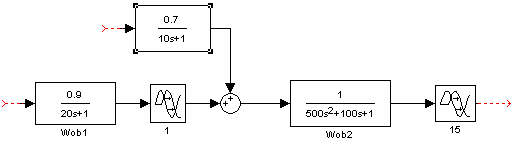
4. Анализ системы с учетом нелинейности 4.1 Определение автоколебаний в системе
Для определения возможности возникновения автоколебаний воспользуемся методом гармонической линеаризации. Суть метода заключается в замене нелинейного элемента эквивалентным линейным. Признак эквивалентности – одинаковость преобразования гармонического входного сигнала. Эквивалентный линейный элемент характеризуется эквивалентным комплексным коэффициентом усиления.
Переход к эквивалентному линейному элементу позволяет исследовать систему частотными методами (можно определить возможность возникновения в системе автоколебаний, а также их параметры).
В системе присутствует симметричная однозначная нелинейность типа “насыщение”.

Рисунок 4.1
![]() , где (4.1)
, где (4.1)
![]() эквивалентный комплексный коэффициент усиления;
эквивалентный комплексный коэффициент усиления;
А- амплитуда автоколебаний.
Для нелинейности типа насыщения ![]() , а
, а
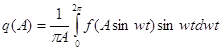
Рассчитаем ЭККУ нелинейного элемента с данными параметрами.
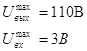
Xвых=f(Xвх)
![]()

(4.2)
Воспользуемся частотным методом анализа симметричных автоколебаний.
В замкнутой системе имеют место незатухающие колебания управляемой величины, при условии:
![]()
![]()
![]() - условие существования симметричных автоколебаний
- условие существования симметричных автоколебаний
На комплексной плоскости строим ![]() . На этой же плоскости по выражению
. На этой же плоскости по выражению ![]() строится годограф инверсного ЭККУ.
строится годограф инверсного ЭККУ.
В системе возникнут автоколебания управляемой величины, если годограф Найквиста и годограф инверсного ЭККУ пересекутся.
Передаточная функция линейной части системы имеет вид:
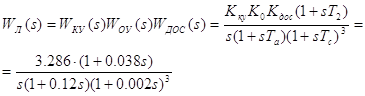
![]()
![]() ;
;
|
| w, | P(w) | Q(w) |
| 1 | -0.285 | -3.252 |
| 10 | -0.122 | 0.189 |
| 100 | -0.0070 | -0.0073 |
|
| 0 | 0 |

Рисунок 4.2
Из рисунка 4.2 видно, что годографы не имеют точек пересечения, следовательно, в системе отсутствуют автоколебания.
4.2 Влияние коэффициента усиления разомкнутой системы на условие возникновения автоколебанийВ замкнутой системе будут возникать автоколебания, если годограф Найквиста будет проходить через точку (-1;j0), т.е. система будет находиться на границе устойчивости. Граница устойчивости будет достигаться при коэффициенте усиления системы, равного критическому, т.е. при К=Ккр=431с-1.
4.3 Анализ абсолютной устойчивости положения равновесия системы по критерию ПоповаЕсли замкнутая система состоит из устойчивой линейной части и одного безынерционного нелинейного элемента со статической характеристикой, расположенной в секторе от 0 до К, то достаточным условием устойчивости положения равновесия системы в начале координат является следующее:
![]() ,
,
где q- произвольное число, использованное для доказательства критерия
К-коэффициент наклона прямой, ограничивающей сектор расположения статической характеристики нелинейного элемента.
Преобразуем АФЧХ линейной части системы, домножив мнимую часть на w.
![]()
![]()
![]()
![]()
![]()
Формулировка критерия: для абсолютной устойчивости положения равновесия системы достаточно, чтобы годограф линейной преобразованной части системы располагался справа от прямой Попова
Т. к. линейная часть системы устойчива, то критерий Попова можно применять напрямую.
Вещественная и мнимая части преобразованной частотной передаточной функции имеют вид:
![]()
![]()
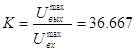
Таблица 4.2
| w, | P(w) | Q(w) |
| 0 | -0,289 | -3,286 |
| 274.36 | -0.0026 | 0 |
| 852.16 | 0 | 0.135 |
|
| 0 | 0 |

Рисунок 4.3
Из Рисунка 4.3 видно, что через точку ![]() нельзя провести прямую, такую, что преобразованная АФЧХ лежала бы справа от этой прямой.
нельзя провести прямую, такую, что преобразованная АФЧХ лежала бы справа от этой прямой.
Следовательно, для системы характерна абсолютная неустойчивость положения равновесия.
Заключение
В результате проведения синтеза была скорректирована система, удовлетворяющая требованиям технического задания. Соответствие приведено ниже в таблице.
Таблица
| Параметр | Техническое задание | Скорректированная система |
| Перерегулирование | не более 20% | 18,8% |
| Время регулирования | не более 0,25с | 0,147 |
Список использованной литературы
1. Бесекерский В.А., Попов Е.П. “Теория систем автоматического регулирования” — М.: Наука, 1972.
2. Зырянов Г.В., Кощеев А.А. “Динамический синтез систем автоматического управления”. Учебное пособие по выполнению курсовой работы.- Челябинск, 2001.
3. Павловская О.О. “Лекции по курсу ТАУ”
Похожие работы
... регулятор на нелинейный элемент. В качестве нелинейного элемента возьмём идеальное реле, статическая характеристика звена изображена на рисунке 23. Рис.23. Идеальное реле Чтобы реализовать данный регулятор в заданной системе автоматического управления, требуется рассчитать значения параметра с. Проанализируем работу системы с нелинейной характеристикой и без неё в Simulink, а затем найдём ...
... ) формирования регулятором регулирующих воздействий в частности, как задача коррекции в нужном направлении динамических свойств регулятора. При этом рассмотрение схем систем автоматического регулирования производится как на основании структурных соображений, т.е. исходя из характера взаимодействия отдельных элементом системы, определяемых лишь видом математического описания этих элементов, так и в ...
... определению: ; Составим диагональные миноры: ; ; Итак, получаем, что ; ; , т.е. условие устойчивости системы не выполняется, а следовательно система по критерию Гурвица неустойчива. 4.2 Исследование устойчивости САУ по критерию Найквиста В соответствии со структурной схемой (рис.3) АЧХ и ФЧХ разомкнутой САУ можно представить в виде произведения АЧХ и суммы ФЧХ элементарных ...
... записи в Zam_ck=inv(l+sysl)*sysl можно в диалоговом режиме произвести новую запись zpk(.) - сокращая одинаковые элементы числителя и знаменателя в Zam_ck. 2.Исследование линейной импульсной системы автоматического управления Задание: 1) Найти передаточные функции импульсной САУ: W*(z) разомкнутой системы, Ф*(z) – замкнутой системы, Фе*(z) – системы по ошибке. Параметры Т, Т1, τ1, К0, ...

0 комментариев