Навигация
1.2 Метод Рунге – Кутта
Пусть дано дифференциальное уравнение первого порядка y`=f(x,y) с начальным условием y(x0)=y0.
Выберем шаг h и введём обозначения:
xi=x0+i*h и yi=y(xi), где i=0,1,2,...,
xi- узлы сетки,
yi- значение интегральной функции в узлах.
Проведём решение в несколько этапов.
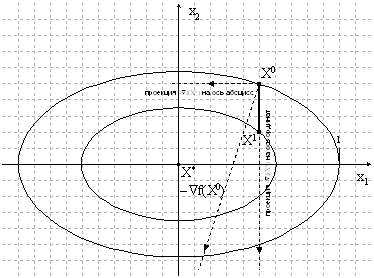
Обозначим точки: A(xi,yi), B(xi+1,yi+1), C, D, E.
Через точку А проведём прямую под углом α, где tg α = f(xi,yi).
На прямой (1) найдём точку С. Через точку С проведём прямую под углом α1, где
tg α1 = f(xi+h/4, yi+h/4*f(xi,yi).
Через точку А проведём прямую параллельную последней прямой.
Найдём точку D на прямой (2) и через неё проведём прямую под углом α2, где
tg α2 = f(xi+h/2, yi+h/2*f(xi,yi)).
Через точку А проведём прямую параллельную последней прямой.
По примеру, описанному выше, построим прямую, которая пересечётся с прямой x = xi+1. Эта точка и будет решением дифференциального уравнения при x = xi+1.
Согласно методу Рунге – Кутта четвёртого порядка, последовательные значения yi искомой функции y определяется по формуле:
y i+1=yi+Δy,
где
Δy=(k1+2*k2+2*k3+k4)/6, i=0,1,2,...
а числа k1(i),k2(i),k3(i),k4(i) на каждом шаге вычисляются по формулам:
k1=h*f(xi,yi)
k2 =h*f(xi+h/2,yi+k1/2)
k3=h*f(xi+h/2,yi+k2/2)
k4 =h*f(xi+h,yi+k3)
Это явный четырёхэтапный метод четвёртого порядка точности.

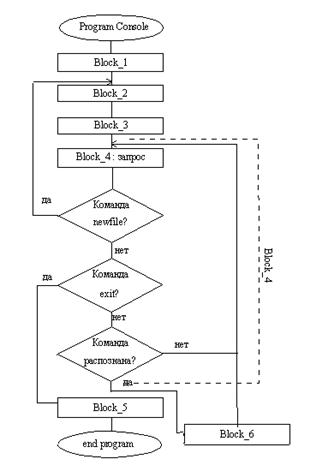
2. Блок-схемы
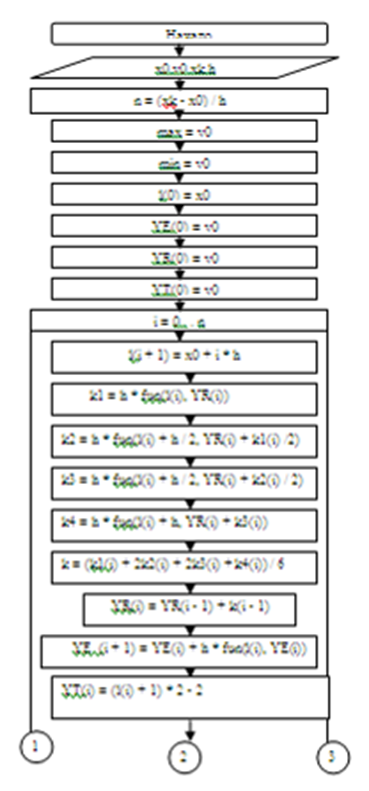
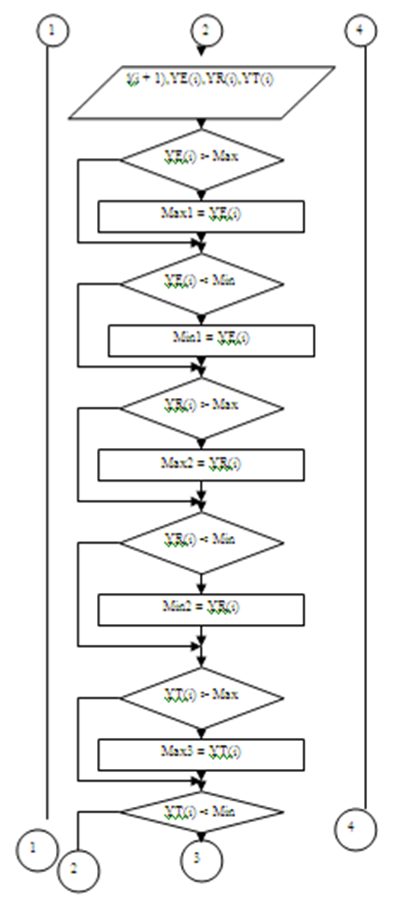

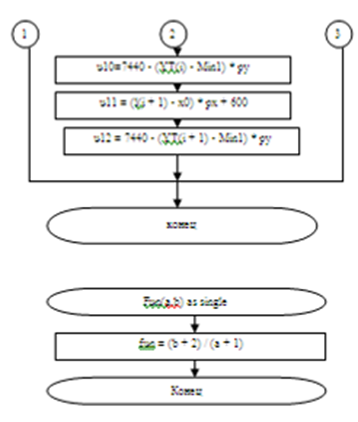
3. Виды, формы
3.1 Начальная форма
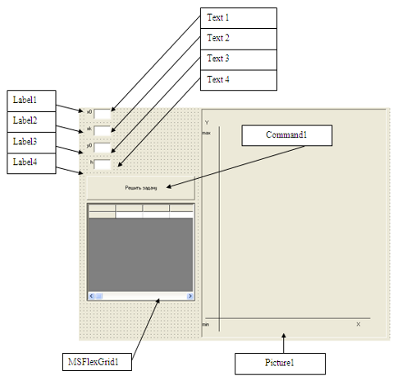
3.2 Конечная форма

4. Программа для решения дифференциального уравнения в Visual Basic
Dim y(9) As Single
Dim YE(9) As Single
Dim YR(9) As Single
Dim YT(9) As Single
Dim l(9) As Single
Private x0 As Single
Private Function fun(a As Single, b As Single) As Single
f = (b + 2) / (a + 1)
fun = f
End Function
Private Sub Command1_Click()
x0 = Val(Text1.Text)
xk = Val(Text2.Text)
y0 = Val(Text3.Text)
h = Val(Text4.Text)
N = (xk - x0) / h
MSFlexGrid1.Rows = N + 2
MSFlexGrid1.TextMatrix(0, 0) = "x"
MSFlexGrid1.TextMatrix(0, 1) = "YE"
MSFlexGrid1.TextMatrix(0, 2) = "YR"
MSFlexGrid1.TextMatrix(0, 3) = "YT"
Min = y0
Max = y0
l(0) = x0
y(0) = y0
YE(0) = y0
YR(0) = y0
YT(0) = y0
For i = 0 To N
l(i + 1) = x0 + i * h
k1 = h * fun(l(i), YR(i))
k2 = h * fun(l(i) + h / 2, YR(i) + k1 / 2)
k3 = h * fun(l(i) + h / 2, YR(i) + k2 / 2)
k4 = h * fun(l(i) + h, YR(i) + k3)
k = (k1 + 2 * k2 + 2 * k3 + k4) / 6
YR(i + 1) = YR(i) + k
YE(i + 1) = YE(i) + h * fun(l(i), YE(i))
YT(i) = (l(i + 1) + 1) * 2 - 2
MSFlexGrid1.TextMatrix(i + 1, 0) = l(i + 1)
MSFlexGrid1.TextMatrix(i + 1, 1) = YE(i)
MSFlexGrid1.TextMatrix(i + 1, 2) = YR(i)
MSFlexGrid1.TextMatrix(i + 1, 3) = YT(i)
If YE(i) > Max Then max1 = YE(i)
If YE(i) < Min Then min1 = YE(i)
If YR(i) > Max Then Max2 = YR(i)
If YR(i) < Min Then Min2 = YR(i)
If YT(i) > Max Then Max3 = YT(i)
If YT(i) < Min Then Min3 = YT(i)
Next i
For i = 0 To N - 1
px = (5415 / (xk - x0))
py = (6705 / (max1 - min1))
u1 = (l(i) - x0) * px + 600
u2 = 7440 - (YE(i) - min1) * py
u3 = (l(i + 1) - x0) * px + 600
u4 = 7440 - (YE(i + 1) - min1) * py
Picture1.Line (u1, u2)-(u3, u4)
u5 = (l(i) - x0) * px + 600
u6 = 7440 - (YR(i) - min1) * py
u7 = (l(i + 1) - x0) * px + 600
u8 = 7440 - (YR(i + 1) - min1) * py
Picture1.Line (u5, u6)-(u7, u8)
u9 = (l(i) - x0) * px + 600
u10 = 7440 - (YT(i) - min1) * py
u11 = (l(i + 1) - x0) * px + 600
u12 = 7440 - (YT(i + 1) - min1) * py
Picture1.Line (u9, u10)-(u11, u12)
Next i
End Sub
Заключение
В данной курсовой рассматривались два метода решения ОДУ с начальными условиями, то есть задачи Коши: метод Эйлера и метод Рунге – Кутта четвёртого порядка.
Данные полученные этими методами идентичны друг другу, но с точки зрения простоты использования метод Эйлера гораздо проще в описании, чем метод Рунге – Кутта четвертого порядка.
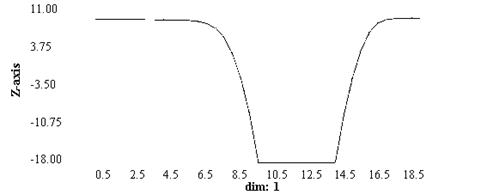
Если посмотреть на графики и значения в точках, то можно убедится в том что методы почти точно определяют значения в у, и графики почти совпадают, имея небольшой угол отклонения.
Похожие работы
... . В добавок, собрание геномов и аннотация их модели может быть представлена путем сравнения положения неизвестного гена и его гомологической последовательности из одного организма в другой, который имеет готовые или хорошо аннотированные последовательности генома. Ниже мы опишем методы визуализации, которые используются для отображения синтении на микро и макро уровнях (таб.3). Визуализация ...
... работы со справочной системой работа практикума приостанавливается. 3. Организационно-экономическое обоснование проекта В ходе дипломного проекта был разработан компьютерный лабораторный практикум по курсу «Теория оптимизации и численные методы». В данном разделе рассмотрена экономическая сторона проекта. Рассмотрены следующие вопросы: 1) сетевая модель 2) расчёт ...
... приложением DOS, то имеет недружелюбный интерфейс, однако является достаточно мощным. Кроме вышеназванных пакетов и программ есть еще множество других средств для визуализации инженерных и научных расчетов – от сложных и универсальных, до простых, узкоспециальных. Но для своих специфических применений разработчики отдельных подсистем САПР разрабатывают свои пакеты или покупают и настраивают уже ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...


0 комментариев