Навигация
Декартова система координат на плоскости. Прямая и окружность
1.5. Декартова система координат на плоскости. Прямая и окружность.
Определение. Декартовой (или ортонормированной, или прямоугольной) системой координат на плоскости называется такая аффинная система координат, базисные векторы которой ортонормированны, то есть имеют единичные длины и ортогональны (перпендикулярны). Обозначение R = {O, i(а), j(а)}; так что |i(а)| = |j(а)| = 1, i(а) перпендикулярен j(а).
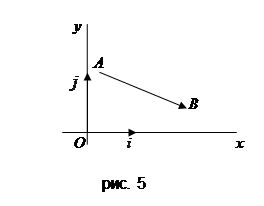 При решении задач, в которых существенную роль играет понятие расстояния между двумя точками, применяется, декартова или прямоугольная система координат.
При решении задач, в которых существенную роль играет понятие расстояния между двумя точками, применяется, декартова или прямоугольная система координат.
Пусть даны две точки: А(х1, у1) и В (х2, у2). Тогда, как известно,
![]() .
.
Пользуясь формулой, запишем уравнение окружности с центром в точке С (a, b) и радиусом r:
![]() .
.
Вышеизложенная теория прямой справедлива и для прямоугольной системы координат. В частности, при решении задач пользуются уравнением прямой с угловым коэффициентом k, проходящей через точку А(х1, у1):
![]() .
.
Отсюда следует, что угловой коэффициент прямой, заданной двумя точками А(х1, у1) и В (х2, у2), вычисляется по формуле
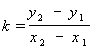
 Угловой коэффициент в прямоугольной системе координат имеет следующий геометрический смысл:
Угловой коэффициент в прямоугольной системе координат имеет следующий геометрический смысл: ![]() , где
, где ![]() – величина угла от оси абсцисс до прямой l.
– величина угла от оси абсцисс до прямой l.
Пусть прямые l1 и l2 заданы своими уравнениями с угловыми коэффициентами: у = k1х + b1 и у = k2х + b2.
Если l1 || l2, то ![]() , поэтому k1 = k2, и обратно, т.е. условие k1 = k2 выражает признак параллельности прямых l1 и l2.
, поэтому k1 = k2, и обратно, т.е. условие k1 = k2 выражает признак параллельности прямых l1 и l2.
Введем формулу для вычисления угла ![]() между пересекающимися прямыми l1 и l2 (рис. 6).
между пересекающимися прямыми l1 и l2 (рис. 6).
Так как ![]() и
и ![]() ,
, ![]() , то
, то

или

Полученную формулу для вычисления угла от прямой l1 до прямой l2 можно записать и так:
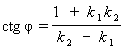
Отсюда следует, что ![]() тогда и только тогда, когда k1k2 = - 1, т.е. условие k1k2 = - 1 выражает признак перпендикулярности прямых l1 и l2.
тогда и только тогда, когда k1k2 = - 1, т.е. условие k1k2 = - 1 выражает признак перпендикулярности прямых l1 и l2.
Приступая к решению геометрической задачи, следует рационально выбрать систему координат, присоединить её к данной фигуре наиболее естественным образом. Желательно, чтобы данные точки располагались на осях координат, тогда среди координат будут нули. Это позволит упростить вычисления.
1.6. Аналитическое задание геометрических фигур.Аналитическое условие и геометрические фигуры.
После того как на плоскости введена система координат, мы получаем возможность рассматривать на этой плоскости такие множества точек (а они - то и образуют те или иные геометрические фигуры), координаты х, у которых удовлетворяют тем или иным условиям (ограничениям). Эти условия могут носить характер уравнений, неравенств или систем уравнений и неравенств. Обратно, если на плоскости имеется некоторая геометрическая фигура (т.е. некоторое множество точек этой плоскости), то возникает задача нахождения аналитических условий, связывающих координаты х, у точек плоскости, которым удовлетворяют координаты всех точек данной фигуры и не удовлетворяют координаты никаких точек плоскости, не принадлежащих этой фигуре.
Аналитические условия, связывающие две переменных х, у и характеризующие фигуры Ф, с точки зрения математической логики представляют собой двухместный предикат Р(х, у), заданный на множестве вещественных чисел: х, у Î R. Множество истинности этого предиката как раз и представляют собой такое множество пар действительных чисел х, у, которые служат координатами точек фигуры Ф и только таких точек. Этот факт записывают следующим образом:
Ф = {М(х, у): Р(х, у) – истинно}.
При этом, нетрудно понять, что если предикат Р(х. у) представляет собой конъюнкцию двух предикатов P1(х, у) Ù Р2 (х, у), то фигура Ф есть пересечение двух фигур Ф = {М (х, у): Р1 (х, у) Ù Р2 (х, у) – истинно} = {М (х, у): Р1 (х, у) – истинно} Ç {М (х, у): Р2 (х, у) – истинно} = Ф1 Ç Ф2.
Аналогично, если предикат Р(х, у) представляет собой дизъюнкцию двух предикатов P1(х, у) Ú Р2 (х, у), то фигура Ф есть объединение фигур Ф = Ф1 È Ф2.
Итак, при координатном подходе к изучению геометрических фигур выделяются две взаимно обратные задачи:
Похожие работы
... учебник и задачник / А. П. Кисилев, Н.А. Рыбкин. – М.: Дрофа, 1995. 9. Изучение личности школьника / под. ред. Л.И. Белозеровой. – Киров, Информационный центр, 1991. 10. Коновалова, В.С. Решение задач на построение в курсе геометрии как средство развития логического мышления / В.С. Коновалова, З.В. Шилова // Познание процессов обучения физике: сборник статей. Вып.9. – Киров: Изд-во ...
... 1. Точки М и N — середины диагоналей АС и BD четырехугольника ABCD. (Рис.1)Доказать, что |AB|2+|BC|2+|CD|2+|DA|2 = |AC|2+|BD|2+4|MN|2.Решение. Пусть точкам A, В, С, D, М, N соответствуют комплексные числа а, b, с, d, т, п.Так как m = и n = , то |AB|2+|BC|2+|CD|2+|DA|2 |AC|2+|BD|2+4|MN|2 .Равенство доказано.Задача 2. Доказать, что если в плоскости параллелограмма ABCD существует такая точка М, ...
... , основанной на поглощении атомами рентгеновского излучения. Ультрафиолетовая спектрофотометрия — наиболее простой и широко применяемый в фармации абсорбционный метод анализа. Его используют на всех этапах фармацевтического анализа лекарственных препаратов (испытания подлинности, чистоты, количественное определение). Разработано большое число способов качественного и количественного анализа ...
... координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных изображений. Можно выделить следующие цели изучения метода координат в школьном курсе геометрии: - дать учащимся эффективный метод решения задач и доказательства ряда теорем; - показать на основе этого метода тесную связь алгебры и геометрии; - способствовать ...

0 комментариев