Навигация
FORMAT(1Х,'ТНЕ EIGENVALUES ARE'')
100 FORMAT(1Х,'ТНЕ EIGENVALUES ARE'')
101 FORMAT(1X,E15.8)
STOP
END
Результат работы программы получаем в виде:
Собственные значения равны
0.33709179E 08
0.19149061E 08
0.71417603E 07
Метод Гивенса для симметричных матриц
Метод Гивенса основан на преобразовании подобия, аналогичном применяемому в методе Якоби. Однако в этом случае алгоритм построен таким образом, что вновь образованные нулевые элементы при всех последующих преобразованиях сохраняются. Поэтому метод Гивенса требует выполнения конечного числа преобразований и по сравнению с методом Якоби связан с меньшими затратами машинного времени. Его единственный недостаток состоит в том, что симметричная матрица приводится не к диагональному, а к трехдиагональному виду. Ниже будет показано, что такая форма матрицы может быть весьма полезной и оправдывает усилия, затраченные на ее получение.
В случае матрицы размерности п х п метод Гивенса требует п — 2 основных шагов, на каждом из которых выполняется ряд преобразований, число которых зависит от числа нулей, которое хотят получить в данном столбце или строке. На k -м шаге обращают в нули элементы, стоящие вне трех диагоналей k-й строки и k -го столбца, сохраняя в то же время нулевые элементы, полученные на предыдущих шагах. Таким образом, перед началом k -го шага преобразованная матрица является трехдиагональной, если ограничиться рассмотрением ее первых k — 1 строк и столбцов. По мере преобразований симметричная матрица размерности 5х5 приобретает следующие формы:
| * | * | * | * | * | ||
| * | * | * | * | * | ||
| A0= | * | * | * | * | * | исходная матрица, |
| * | * | * | * | * | ||
| * | * | * | * | * |
| * | * | 0 | 0 | 0 | ||
| * | * | * | * | * | ||
| A1= | 0 | * | * | * | * | после первого основного шага, |
| 0 | * | * | * | * | состоящего из трех преобразований, | |
| 0 | * | * | * | * |
| * | * | 0 | 0 | 0 | ||
| * | * | * | 0 | 0 | ||
| A2= | 0 | * | * | * | * | после второго основного шага, |
| 0 | 0 | * | * | * | состоящего из двух преобразований, | |
| 0 | 0 | * | * | * |
| * | * | 0 | 0 | 0 | ||
| * | * | * | 0 | 0 | после третьего основного шага, | |
| A3= | 0 | * | * | * | 0 | состоящего из одного преобразования. |
| 0 | 0 | * | * | * | Теперь матрица имеет трехдиагональный вид. | |
| 0 | 0 | 0 | * | * |
На каждом основном шаге изменяются лишь те элементы матрицы аij, которые расположены в ее правой нижней (заштрихованной) части. Таким образом на k-м шаге преобразуется только матрица порядка (п — k + 1), занимающая правый нижний угол исходной матрицы. Ясно, что на каждой следующей стадии выполняется меньшее число преобразований, чем на предыдущей. Всего для приведения матрицы к трехдиагональному виду требуется выполнить (n2 — Зп + 2)/2 преобразований.
Наш опыт применения метода Гивенса показывает, что можно при выполнении одного шага преобразований обратить в нуль сразу все элементы целой строки и столбца, стоящие вне трех диагоналей матрицы. Метод, позволяющий выполнить такое преобразование, предложил Хаусхолдер .
Метод Хаусхолдера для симметричных матриц
Метод Хаусхолдера позволяет привести матрицу к трехдиагональному виду, выполнив почти вдвое меньше вычислений по сравнению с другими методами. Это обусловлено тем, что при его применении становятся нулевыми сразу все элементы строк и столбцов, стоящие вне трех диагоналей матрицы. Метод Хаусхолдера позволяет получить требуемый результат быстрее, чем метод Гивенса, так как связан с выполнением меньшего числа, хотя и более сложных преобразований. Это его свойство особенно ярко проявляется применительно к большим матрицам. Хотя в методе Хаусхолдера вместо плоских вращении используются эрмитовы ортогональные преобразования матриц, трехдиагональная форма матрицы, которую получают этим методом, имеет те же собственные значения, что и трехдиагональная матрица, получаемая методом Гивенса. При использовании метода Хаусхолдера на п — 2 основных шагах выполняются следующие преобразования:
Аk = РkAk-1Рk, k=1, 2, ..., п-2,
где Aо == А.
Каждая преобразующая матрица имеет вид
uk ukT
Pk = E - -------------- ,
2Kk2
где
ui,k = 0 при i = 1, 2, …, k,
ui,k = ak,i при i = k+2, …, n,
uk+1,k = ak,k+1 ± Sk.
Здесь
![]()
![]() n 1/2
n 1/2
Sk = S a2k,i
i=k+1
2K2k = S2k ± ak, k+1 Sk.
В этих уравнениях берется знак, соответствующий элементу ak,k+1. Это позволяет сделать значение иk+1,k максимальным. Отметим, что методами Гивенса и Хаусхолдера можно пользоваться и в случае несимметричных матриц, приводя их, правда, не к трехдиагональному, а другому частному виду треугольной матрицы известной как матрица Гессенберга:
| * | * | 0 | 0 | 0 | 0 |
| * | * | * | 0 | 0 | 0 |
| * | * | * | * | 0 | 0 |
| * | * | * | * | * | 0 |
| * | * | * | * | * | * |
| * | * | * | * | * | * |
Похожие работы
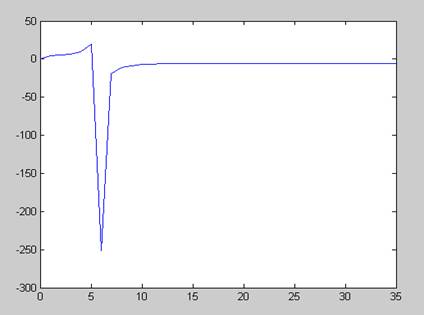
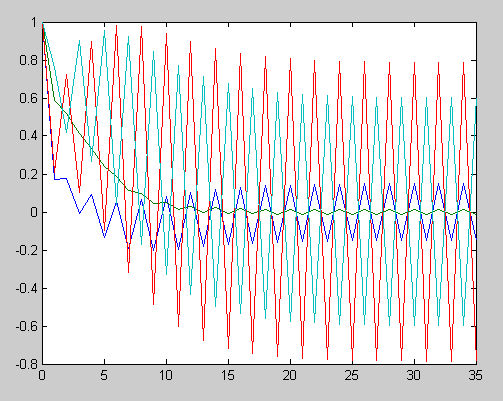
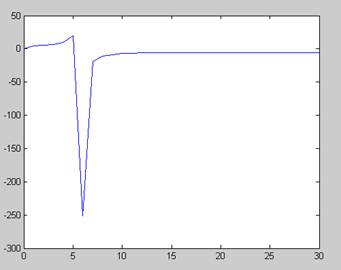
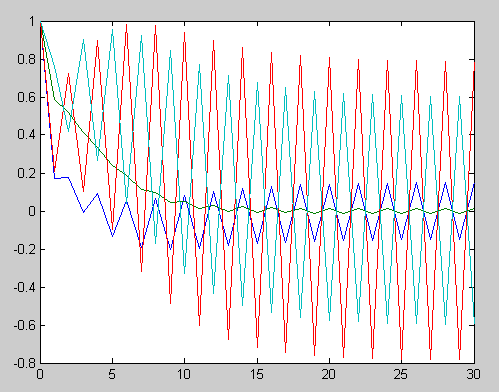
... 0135 0.7866 -0.5989 График значений собственного числа заданной матрицы за время итерационного процесса/ График значений собственного вектора, соответствующего собственному числу Рассмотрим другие примеры: Исходные данные: yn=[1,1,1]; L1= 0.01 edop=0.00001; a=[1 1 1; 2 3 4; 0 4 0]; Найдем собственные значения исходной матрицы, используя функцию eig. Получим L1= 6.2085 ...
... решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n - ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с ...
... степень изношенности дисков, налипание к валу инородных предметов и так далее, то обратная задача состоит в диагностировании характеристик вала с дисками по собственным частотам колебаний вала. Известно, что изменения указанных значений характеристик вала проявляются в изменениях значений собственных частот его колебаний, что в свою очередь может привести к ненужным вибрациям, увеличению шума и т. ...
... собственных значений сводится к проблеме раскрытия определителя по степеням и последующему решению алгебраического уравнения m- й степени. Определитель называется характеристическим (или вековым ) определителем, а уравнение (2) называется характеристическим (или вековым ) уравнением. Различают полную проблему собственных значений, когда необходимо отыскать все собственные значения ...
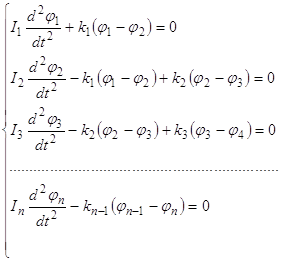
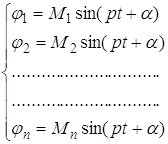

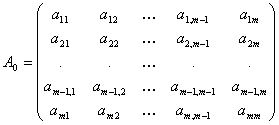
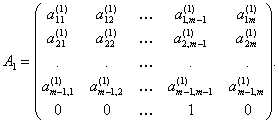

0 комментариев