Навигация
1 a1>0 1 a1>0 1 a1< 0
(x, 1) a=1 a >1 (x, a) 0< a<1
(0, b)
x x x
0 – ¥ 1 0 – ¥ 1 0 – ¥ 1
Для игрока 2 исследования аналогичны. Если ввести обозначения
b1 := b11 - b12 - b21 + b22
b2 := b22 - 
то множество L приемлемых для него ситуаций состоит из :
всех ситуаций вида (x, 0), если b1x - b2 < 0; 0 £ x £ 1,
всех ситуаций вида (x, y), если b1x - b2 = 0; 0 £ x £ 1; 0 < y < 1,
всех ситуаций вида (x, 1), если b1x - b2 > 0; 0 £ x £ 1.
Результаты следующие :
если b1 = b2 = 0, то решение 0 £ x £ 1; 0 £ y £ 1;
если b1 = 0; b2 ¹ 0, то решение либо y = 0, либо y = 1 при 0 £ x £ 1 (приемлемой стратегии в игре не существует);
если b1 > 0, то решения следующие :
y = 0, x < 
= b; y = 1,
x > b; 0 < y < 1; x = b;
если b1 < 0, то решения следующие :
y = 0, x > b; y = 1, x < b; 0 < y < 1; x = b
При этом необходимо учитывать, что 0 £ x £ 1.
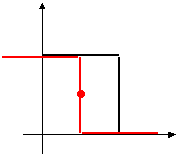
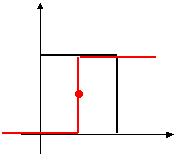y y
1 1
(b,y) (b,y)
x x
0 1 0 1
b1 > 0 b1 < 0
0 < b < 1 0 < b < 1
Решением игры является пересечение множеств K и L, т.е. те значения x и y, которые являются общими для множеств K и L.
y y
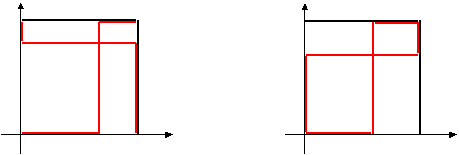1 1
x x
0 1 0 1
а) б)
При этом зигзаги K и L могут быть не только одинаковой, но и противоположной направленности. В первом случае зигзаги имеют одну точку пересечения, а во-втором – три. Средние выигрыши при этом определяются по формулам (*), если в них подставить полученное решение x и y (рис.а)). Очевидно a входит в смешанную стратегию игрока 2, хотя зависит только от выигрышей 1 игрока; b входит в смешанную стратегию игрока 1, хотя зависит только от выигрышей игрока 2. Сравнение этих результатов с результатами решения матричных игр с нулевой суммой показывает, что a совпадает с оптимальной стратегией игрока 1 в матричной игре с матрицей A, а b – с оптимальной стратегией игрока 2 в матричной игре с матрицей B. Отсюда можно сделать вывод, что равновесная ситуация направляет поведение игроков не только на максимизацию своего выигрыша, сколько на минимизацию выигрыша противника.
С другой стороны, естественно также рассматривать подходящим поведение игроков в конечных бескоалиционных играх, направленное на максимизацию своего выигрыша с учётом максимального противодействия игрока, т.е. подходящей стратегией игрока 1 считать оптимальную смешанную стратегию игрока 1 в матричной игре с матрицей A, а подходящей стратегией игрока 2 считать оптимальную смешанную стратегию игрока 2 в матричной игре с матрицей B, если в ней рассматривать решение с позиций максимизации выигрыша игрока 2, т.е. решать её, как для игрока 1, с матрицей 
.
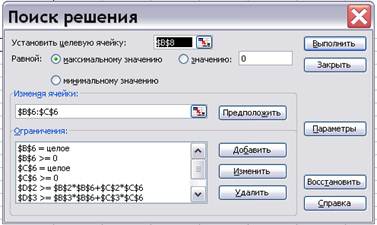
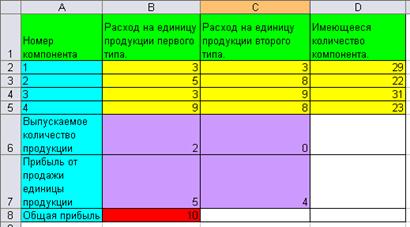
Пример1. Министерство желает построить один из двух объектов на территории города. Городские власти могут принять предложения министерства или отказать. Министерство – игрок 1 – имеет две стратегии: строить объект 1, строить объект 2. Город – игрок 2 – имеет две стратегии: принять предложение министерства или отказать. Свои действия (стратегии) они применяют независимо друг от друга, и результаты определяются прибылью (выигрышем) согласно следующим матрицам :
A = 
, B = 
(например: если игроки применяют свои первые стратегии, министерство решает строить 1 объект, а городские власти разрешают его постройку, тогда город получает выигрыш 5 млн, а министерство теряет 10 млн, и т.д.)
Решение. Для этой игры имеем :
a1 = a11 - a12 - a21 + a22 = -10 - 2 - 1 - 1 = -14 < 0,
a2 = a22 - a12 = -1 - 2 = -3,
.
Так как a1 < 0, то множество решений K имеет следующий вид :
(0, y) при 
;
(x, 
) при 0 £ x £ 1;
(1, y) при 0 £ y £ 
.
Для 2 игрока имеем :
b1 = b11 - b12 - b21 + b22 = 
5 + 2 + 1 + 1 = 9 > 0,
b2 = b22 - b21 = 1 + 1 = 2,
.
y
1
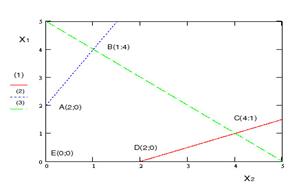
Так как b1 > 0, то множество решений L L
имеет следующий вид :
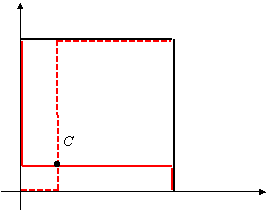
K
(x; 0), при 0 £ x £
; 
(
; y), при 0 £ y £ 1; 0 
1 x
(x; 1), при 
£ x £ 1.
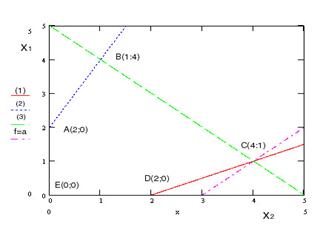
Точка пересечения множеств L и K есть точка C с координатами x = 
; y = 
и является соответственно приемлемыми стратегиями министерства и города.
При этом выигрыш соответственно равен
E1(A,x,y) = (x, 1-x)
=
= 
= 
E2(A,x,y) = (x, 1-x)
= 
Замечание. Если решить эту игру как матричные игры двух игроков с нулевой суммой, то для игры с матрицей A оптимальные смешанные для 1 игрока и цена игры получаются из решения уравнений
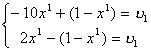
откуда вероятность применения игроком 1 первой стратегии равна 
, цена игры – 
, что совпадает с E1, вероятность применения игроком 2 первой стратегии 
; для игры с матрицей B оптимальные смешанные стратегии и цена игры для игрока 2 определяются из системы :
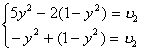
Следовательно, вероятность применения игроком 2 своей стратегии 
, а игроком 1
, цена игры 
, что совпадает с E2.
Таким образом, если каждый из игроков будет применять свои стратегии в этой игре, исходя только из матриц своих выигрышей, то их оптимальные средние выигрыши совпадают с их выигрышами при ситуации равновесия.
Похожие работы
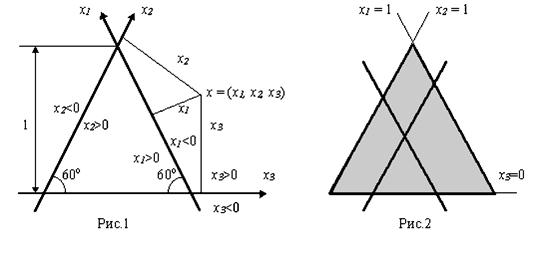
р, на основе недостаточных данных) можно интерпретировать как конфликт принимающего решения субъекта с природой. Поэтому Теория игр рассматривается также как теория принятия оптимальных решений в условиях неопределённости. Она позволяет математизировать некоторые важные аспекты принятия решений в технике, сельском хозяйстве, медицине и социологии. Перспективен подход с позиций Теории игр к ...
... на множествах коалиций двух игроков произвольные (здесь нет условия дополнительности) u(1,2) = C3, u(1,3) = C2, u(2,3) = C1, но удовлетворяющие условию 0 £ C1, C2, C3 £ 1. Таким образом, классы стратегической эквивалентности общих кооперативных игр трёх игроков могут быть поставлены в соответствие точкам трёхмерного единичного куба подобно тому, как это получилось для игр 4-х ...
... запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличение запасов, гарантирующих бесперебойную работу производства, сокращения запасов в целях минимизации затрат на их хранение. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как посева одной из возможных культур, урожай которой зависит от погоды, если известны цена единицы ...
... R:=maximize(f,C ,NONNEGATIVE ); Ø f_max:=subs(R,f); Ø R1:=minimize(f,C ,NONNEGATIVE ); f_min:=subs(R1,f); ОТВЕТ: При x1=5/4 x2=5/4 f_max=15/4; При x1=0 x2=0 f_min=0; Урок № 5.Решение матричных игр, используя методы линейного программирования и симплекс метод Тип урока: урок контроль + урок изучения нового материала. Вид урока: Лекция. Продолжительность: ...
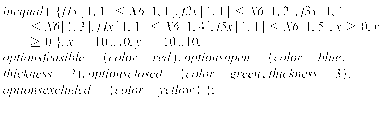
0 комментариев