Навигация
0 и записывать 
при →0,
если 
при →0.
Степенные ряды – это специальный случай рядов в нормированном пространстве, когда члены ряда зависят от параметра.
Рассмотрим в нормированном пространстве X ряд вида 
, где xк Î X, а – вещественное или комплексное переменное. Поскольку можно ввести новую переменную –0 = 
, то в дальнейшем мы полагаем 0 = 0 и рассматриваем степенные ряды вида
(1)
Конечная сумма 
называется частичной суммой степенного ряда (1).
Пусть 
– множество всех точек 
, для которых ряд (1) сходится. называется областью сходимости ряда (1).
Сумму ряда (1) при Î обозначим через S() (это абстрактная функция, определенная на со значениями в X), при этом будем писать
, при Î .
Последнее равенство означает, что Sn() → S() при n→∞ для всех Î .
Очевидно, область сходимости любого степенного ряда (1) не пуста, так как 0 Î . Как и в случае скалярных функций, справедлива следующая теорема.
Теорема 10 (Абель). Пусть0 ≠ 0 и 0 Î , тогда круг 
содержится в . Во всяком круге Sr(0), где r < 
, ряд (1) сходиться абсолютно и равномерно относительно .
Теорема 11. Пусть два степенных ряда равны в круге SR(0), R>0:
;
тогда равны все их коэффициенты: 
(k=0, 1, 2, …)
Дифференцирование абстрактных функций
Пусть функция 
числового переменного λ со значениями в банаховом пространстве X определена в окрестности точки λ0.
По определению производной x’(λ0) функции x(λ) в точке λ0 называется предел
,
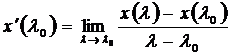если этот предел существует (и конечен). Если имеет производную в точке λ0, то она называется дифференцируемой в этой точке.
§5. Аналитические абстрактные функции и ряды Тейлора
Абстрактную функцию x() будем называть аналитической при =0, если она представима в некоторой окрестности точки =0 сходящимся степенным рядом:
(1)
с ненулевым радиусом сходимости.
Теорема 12. Если x() – аналитическая абстрактная функция при =0, то x() непрерывна в круге SR(0), где R – радиус сходимости степенного разложения (1).
Теорема 13. Если x() – аналитическая абстрактная функция при =0, то x() дифференцируема в круге SR(0) сходимости своего степенного разложения.
Пусть x() бесконечно дифференцируема в точке 0. Ряд вида
называется рядом Тейлора функции x().
Если x() аналитична при =0, то ее ряд Тейлора, в силу теоремы 10, является ее степенным разложением и, значит, сходится к ней в SR(0).
Понятие абстрактной аналитической функции используется в широко применяемом на практике методе малого параметра.
§6. Метод малого параметра в простейшем случае
Рассмотрим следующее уравнение:
Аx –Сx=y. (1)
Здесь А, С Î L(X,Y) и y Î Y заданы, - скалярный параметр, 
, а неизвестное x разыскивается в X. Если 
, т.е.
, (2)
то, согласно теореме 9, оператор А–С непрерывно обратим, и тогда решение уравнения (1) существует, единственно и задается явной формулой
. (3)
Отсюда видно, что в круге (2) решение является аналитической функцией параметра и, следовательно, может быть найдено в виде
(4)
На этой идее основывается метод малого параметра для уравнения (1). Подставим ряд (4) в уравнение (1) и, согласно теореме единственности разложения в степенной ряд, приравниваем коэффициенты при одинаковых степенях в правой и левой частях получившегося тождества:
.
Таким образом, мы приходим к следующей рекуррентной системе уравнений для определения x0, x1, …:
Аx0=y, Аx1=Сx0, …, Аxк=Сxк-1, …
Так как А непрерывно обратим, то отсюда последовательно находим
x0=А–1y, x1= А–1(СА–1)y, …, xк= А–1(СА–1)кy, …
Следовательно,
. (5)
Мы получили решение (3), разложенное в степенной ряд. Если мы хотим оборвать степенной ряд и ограничиться приближенным решением
то можно оценить ошибку. Вычитая из ряда (5) его частичную сумму (6) и оценивая разность по норме, получим
.
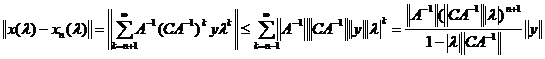§7. Метод малого параметра в общем случае
Пусть дано уравнение
А(
)х = у(). (1)
Здесь А()Î L(X,Y) задана при каждом , , или, как говорят, А() – оператор-функция. Пусть А() аналитична при =0, а оператор А(0) непрерывно обратим, у() – заданная аналитическая функция при =0 со значениями в Y. Неизвестное x разыскивается в X.
Аналитичность А() и у() в точке 0 означает, что они разлагаются в следующие степенные ряды с ненулевыми радиусами сходимости, которые равны 
и 
соответственно:
, 
. (2)
Из аналитичности А() следует непрерывность А() при =0. следовательно, найдется число r > 0 такое, что в круге 
.
Отсюда вытекает, что в круге оператор-функция А() непрерывно обратима и, следовательно, уравнение (1) имеет единственное решение
,
при этом x() аналитична в точке =0 и радиус сходимости соответствующего степенного ряда равен min(, r). Для фактического построения x() удобно воспользоваться методом малого параметра. Будем разыскивать x() в виде
. (3)
Подставляя ряд (3) в уравнение (1) и учитывая разложения (2), приходим к следующей системе для неопределенных коэффициентов x0, x1, x2, …:
А0x0 = y0, А0x1+А1x0 = y1,
А0x2 + А1x1 + А2x0 = y2, (4)
. . . . . . . . . . .
, …
Здесь А0 = А(0) непрерывно обратим. Решая последовательно уравнения получившейся системы, находим
, 
, … (5)
Возникающие здесь формулы довольно громоздки, однако этим путем можно найти решение уравнения с любой степенью точности. Метод малого параметра особенно удобен в тех случаях, когда обращение оператора А(0) – задача более простая, чем задача обращения оператора А().
§8. Метод продолжения по параметру
Похожие работы
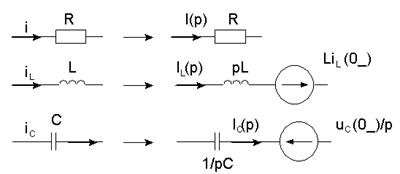
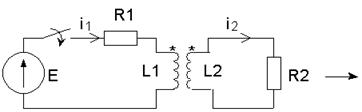
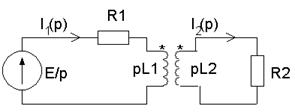
... математических методов, связанных с описанием и анализом типичных явлений, протекающих именно в электротехнических устройствах. 1 Применение преобразования Лапласа и его свойств к расчету переходных процессов Этот метод основан на преобразовании Лапласа. Пусть f(t) – оригинал, а F(p) – изображение этого оригинала по Лапласу. Для сокращения применяют такие обозначения: f(t)F(p), F(p)= Прямое ...
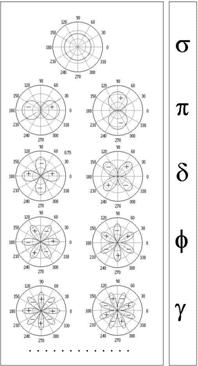
... лишь угловую часть лапласиана и имеет вид: . (6.23) Уравнение Лежандра, встречается в нескольких фундаментальных задачах: 1) в задаче о квантовых состояниях и энергетических уровнях ротатора - линейной молекулы, свободно вращающейся вокруг центра массы. 2) в уравнении Шрёдингера для атома H и водородоподобных ионов. 6.7.3. Уравнение Лежандра это вполне типичное операторное уравнение на
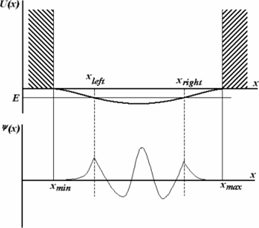
... плотность тока вероятности .(1.9) Из (1.9) следует, что j = 0 для всех функций , у которых функция Ф не зависит от координат. В частности, j= 0 для всех действительных функций . Решения уравнения Шредингера (1.1) в общем случае изображаются комплексными функциями. Использование комплексных функций весьма удобно, хотя и не необходимо. Вместо одной комплексной функции состояние системы можно ...
... популяции обязательно вырождаются, причем независимо от начального распределения особей по возрасту. В завершение рассмотрим пример. Одной из классических моделей динамики популяций является так называемая логистическая модель или модель Ферхюльста, которая описывается дифференциальным уравнением с начальным условием , где , см., например, [5, c. 14]. Если учитывать ограниченность времени жизни ...
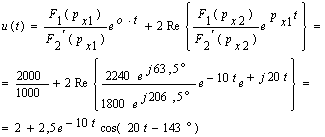
0 комментариев