Навигация
3. Канонический базис
Для дальнейших результатов нам понадобится новый базис W(S), обладающий кроме ортогональности еще некоторыми дополнительными свойствами. Так как ортогональных базисов в гильбертовом пространстве W(S) существует бесконечно много, то любой из них можно получить из последовательности {ek,fk} унитарным преобразованием с матрицей перехода Т. Воспользуемся этим и трансформируем наш базис в базис {l}, ортогональный не только в W(S), но и в следующем скалярном произведении:
|
|
где KR(x0,y0) - шар с центром в (x0,y0) и радиуса R, равного расстоянию от центра до границы S. Базис с таким дополнительным свойством назовем каноническим в точке (x0,y0). Доказано (см.[4]), что базис в W(S), канонический в точке (x0,y0), существует.
Вектор-столбец ![]() бесконечной высоты с координатами:
бесконечной высоты с координатами:
|
| (3.1) |
для l = 0,1,2,... - назовем нормированным следом u(x,y) в точке (x0,0) аналогично его определению в [4].
Ортонормированному базису {ek,fk} сопоставим бесконечную матрицу ![]() , столбцы которой являются нормированными следами в (x0,0) функций ek и fk. Матрица
, столбцы которой являются нормированными следами в (x0,0) функций ek и fk. Матрица ![]() - это нормированная фундаментальная матрица следов (ФМС) в точке (x0,0). Из [4] известно, что
- это нормированная фундаментальная матрица следов (ФМС) в точке (x0,0). Из [4] известно, что![]() разложима в произведение трех сомножителей, первый из которых Q = (qij) частично изометричен в l2, второй - диагонален с положительной возрастающей последовательностью диагональных элементов {j}, а третий - изометричен в l2, т.е.
разложима в произведение трех сомножителей, первый из которых Q = (qij) частично изометричен в l2, второй - диагонален с положительной возрастающей последовательностью диагональных элементов {j}, а третий - изометричен в l2, т.е.
|
|
Учитывая параметры этого разложения и формулы нахождения коэффициентов ряда [4, §5, теорема 1] и используя свойства скалярного произведения, канонический в точке (x0,0) базис ![]() удобно записать в виде ряда по функциям ek и fk. Тогда при всех натуральных l имеют место равенства:
удобно записать в виде ряда по функциям ek и fk. Тогда при всех натуральных l имеют место равенства:
|
| (3.2) |
| где | (3.3) |
Дифференцирование ek и fk сводится к дифференцированию uk и vk.
4. Приближенное интегрирование гармонических функций
В этом параграфе построим формулы интегрирования произвольной функции из W(S) и базисной последовательности полиномов.
Теорема 4.1. Существует единственная последовательность ![]() такая, что для любой функции u из W(S) и точки (x0,0) луночки S скалярное произведение
такая, что для любой функции u из W(S) и точки (x0,0) луночки S скалярное произведение ![]() конечно и при этом
конечно и при этом
|
| (4.1) |
Последовательность ![]() вычисляется по формулам:
вычисляется по формулам:
|
| (4.2) |
где ![]() базис в W(S).
базис в W(S).
Это утверждение легко доказать, если разбить функцию u(x,y) на две части - четную и нечетную по y и разложить каждую в ряд по каноническому базису W(S). Далее, учитывая определение (3.1) координат вектор-столбца ![]() , производя необходимые преобразования с суммами и учитывая (3.2)-(3.3), получим формулы (4.1).
, производя необходимые преобразования с суммами и учитывая (3.2)-(3.3), получим формулы (4.1).
В формулировке теоремы 4.1 мы вывели представления для коэффициентов D1j и D2j, которые используют интегралы по луночке S. Численное вычисление множителя Al сводится к результатам следующего утверждения. Но сначала условимся об обозначениях.
|
| (4.2) |
Теорема 4.2. Интеграл от полинома uk+1, взятый по луночке S = S(1,2-1), совпадает с приращением функции Qk() на отрезке [1,2], а от полинома vk+1, взятый по той же луночке, равен нулю.
Здесь отметим, что приведенное в §4 приложение системы полиномов является не единственным. Например, ее можно применять в задачах, использующих альтернирующий метод Шварца. Также с их помощью можно находить решения в составных областях на плоскости.
Список литературы
Axler S., Bourdon P., Ramey~W. Harmonic Function Theory. Springer-Verlag, 1992.
Лебедев Н.Н. Специальные функции и их приложения.М.: Гос. изд-во физ.-мат. лит. 1963. 360 с.
Диткин В.А., Прудников А.П. Интегральные преобразования и операционное исчисление. М.:Гос. изд-во физ.-мат. лит. 1961. 523 с.
Васкевич В.Л. Аналоги эрмитовых кубатурных формул для интеграла Дирихле от гармонической функции // Теоретические и вычислительные проблемы в задачах математической физики. Труды ИМ СО РАН, том 24. Новосибирск: Наука, Сибирское отделение, 1994. С. 93-126.
Для подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/
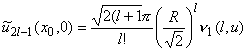 ,
, 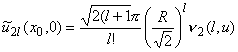 , где
, где 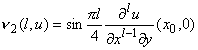
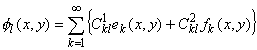
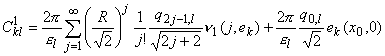
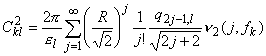
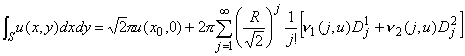
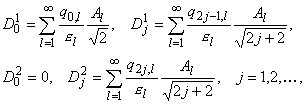
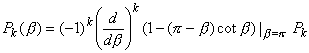
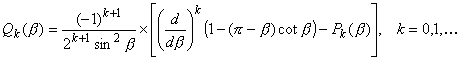
0 комментариев