Навигация
Средняя длительность ожидания
6. Средняя длительность ожидания.
Формула (22) позволяет находить все интересующие нас числовые характеристики длительности ожидания. В частности, математическое ожидание длительности ожидания начала обслуживания или, как предпочитают говорить, средняя длительность ожидания равна
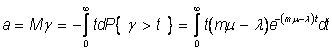
Несложные вычисления приводят к формуле
![]() (23)
(23)
Дисперсия величины g равна
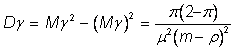 .
.
Формула (23) дает среднюю длительность ожидания одного требования. Найдем среднюю потерю времени требованиями, пришедшими в систему обслуживания в течение промежутка времени T. За время T в систему поступает lT требований в среднем; общая потеря ими времени на ожидание в среднем равна
![]() (24)
(24)
Приведем небольшие арифметические подсчеты, которые продемонстрируют нам, как быстро возрастают суммарные потери времени на ожидание с изменением величины r. При этом мы ограничиваемся случаем T=1 и рассматриваем лишь самые малые значения m: m=1 и m=2.
При m=1 в силу (20)
![]()
При r=0.1; 0.3; 0.5; 0.9; значение al приблизительно равно 0.011; 0.267; 0.500; 1.633; 8.100.
При m=2 в силу (21)
![]()
При r=0.1; 1.0; 1.5; 1.9 значение al приблизительно равно 0.0003; 0.333; 1.350; 17.587.
Приведенные данные иллюстрируют хорошо известный факт относительно большой чувствительности систем обслуживания, уже достаточно сильно загруженных, к возрастанию загрузки. Потребитель при этом сразу ощущает значительное возрастание длительности ожидания. Этот факт обязательно следует учитывать при расчете загрузки оборудования в системах массового обслуживания.[3]
Приложение теории к движению воздушного транспорта
С некоторыми понятиями, связанными с управлением движением воздушного транспорта, мы познакомились в иллюстративном приложении первой главы. Пирси рассмотрел приложения некоторых идей теории массового обслуживания к организации посадки самолетов. В данном случае обычно представляет интерес сокращение времени посадки. Вычислим вначале вероятность того, что один за другим n-1 самолетов ожидают приземления.
Допустим, что самолеты приближаются к зоне управления со случайных направлений через случайные промежутки времени, распределенные по экспоненциальному закону, с постоянной интенсивностью прибытия, которая принимается равной одной единице. Следовательно, e-t - распределение промежутков времени между моментами прибытия. Самолет, который прибывает через промежуток времени, меньший минимального времени, необходимо для безопасного предыдущего самолета, задерживается на минимальное время. Отношение минимального времени, необходимого для безопасной посадки, к средней длительности промежутка времени между прибывающими самолетами обозначается T (для простоты будем считать, что для данного аэропорта эта величина постоянна). Обычно представляет интерес случай T<1. Вероятность того, что прибывший самолет не задерживается, равна
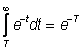 (14.54)
(14.54)
Вероятность того, что будет задержан один самолет, найдем, рассмотрев все задержки одиночных самолетов между двумя незадерживаемыми самолетами. Самолет, который будет задержан, должен прибыть через промежуток времени t1<T после прибытия незадерживаемого самолета, непосредственно предшествующего ему, а незадерживаемый самолет, непосредственно следующий за ним, должен прибыть через промежуток времени t>2T-t1 . Таким образом, искомая вероятность совместного появления этих двух событий равна
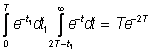
Вероятность того, что будет задержано два самолета, находится аналогично (рассматривается два задерживаемых самолета между двумя незадерживаемыми) путем вычисления вероятности совместного появления событий:
t1 < T - для первого задерживаемого самолета, следующего за незадерживаемым;
t2 < 2T- t1 - для второго задерживаемого самолета, следующего за первым задерживаемым;
t < 3T- t1 - t2 - для незадерживаемого самолета, следующего непосредственно за двумя задерживаемыми.
В результате для двух задерживаемых самолетов получаем
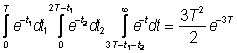 . (14.55)
. (14.55)
Общее выражение для вероятности того, что задерживается n-1 самолетов, имеет вид an Tn-1 e-nT , где an- коэффициент, зависящий только от n. Очевидно, что должно выполняться соотношение
![]() (14.56)
(14.56)
или
![]() (14.57)
(14.57)
где величина UºTe-T для малых T определяется однозначно, следовательно, T можно выразить как функцию от U:
![]() (14.58)
(14.58)
Используя то обстоятельство, что начало координат - кратный полюс, имеем
![]() (14.59)
(14.59)
Следовательно, разложив подынтегральное выражение в ряд и выбрав коэффициент при T-1 , можно найти вычет.
Вероятность того, что один за другим задерживаются n-1 самолетов, равна
![]() (14.60)
(14.60)
Используя формулу Стирлинга для n!, Пирси приводит ряд кривых для этого распределения.
Среднее число самолетов, находящихся в системе (с учетом первого самолета, совершающего посадку без ожидания), равно
![]() (14.61)
(14.61)
Это выражение можно легко найти, дифференцируя выражение (14.56) по T и производя упрощения. (Заметим, что при T=1 задерживаются все самолеты). Аналогично находим второй начальный момент, он равен ![]() .
.
Доля задерживаемых самолетов определяется как отношение среднего числа самолетов, находящихся в системе, без учета самолета, совершающего посадку, к среднему числу самолетов:
![]() .
.
Распределение длительности посадки найдем путем следующих рассуждений. Все промежутки времени длительностью t<T имеют нулевую частоту; промежутки времени длительностью t=T появляются с частотой t; доля задерживаемых самолетов, т.е. доля промежутков времени длительностью t>T, появляется с частотой 1-T появления незадерживаемых самолетов, умноженной на вероятность их прибытия, т.е. на e-(t+T) . Используем единичную функцию H(T- t) (которая равна единице для положительных значений аргумента и равна нулю для отрицательных; ее производная является дельта-функцией) и дельта-функцию d(T-t), чтобы представить это распределение в виде
![]()
Теперь, используя интегральное уравнение Линдли, можно получить распределение времени ожидания. Путем детального анализа Пирси находит выражение для распределения в промежутке времени t, mT < t < (m+1)T:
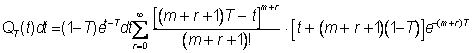
откуда после интегрирования по t (0 £ t £ ¥) он определяет T как долю задерживаемых самолетов. Заметим, что при суммировании по m необходимо рассматривать интервалы (mT,(m+1)T). Отсюда находим также среднее время ожидания
![]() .
.
Заметим, что время ожидания увеличивается с ростом T. Приведенное выше распределение дает критерии для определения необходимой пропускной способности аэропорта.[4]
Список литературыД.Кениг, Д.Штойян. Методы теории массового обслуживания: Пер. с нем. /Под. ред. Г.П.Климова. М., 1981.
Г.И.Ивченко, В.А.Каштанов, И.Н.Коваленко. Теория массового обслуживания. М., 1982.
Б.В.Гнеденко, И.Н.Коваленко. Введение в теорию массового обслуживания. М., 1987.
Т.Л.Саати. Элементы теории массового обслуживания и ее приложения: Пер. с англ. /Под. ред. И.Н. Коваленко, изд-ие 2. М., 19
Похожие работы
... и эффективным средством выработки оптимальных управленческий решений, главной особенностью которых в современных условиях становится их своевременность. 2 Применение теории массового обслуживания в экономическом анализе 2.1 Теория массового обслуживания Теория массового обслуживания – вероятностные модели реальных систем обслуживания населения, при которых время обслуживания будет ...
... сообщение (требование). В таком случае, если в очереди есть сообщения * (требования), переходим в очереди новое состояние: уменьшаем количество сообщений * (требований), ожидающих в обслуживания очереди на 1. */ if (this.getCurrentPort().getName().equals("fromNext")) { serverIsFree = true; /* Если в очереди было одно сообщение (требование), то теперь там не будет ни ...
... коммерческой деятельности. Для решения перечисленных задач существует эффективный метод моделирования, включающий и объединяющий достижения разных наук, в том числе математики. 1.2 Моделирование систем массового обслуживания Переходы СМО из одного состояния в другое происходят под воздействием вполне определенных событий - поступления заявок и их обслуживания. Последовательность появления ...
... сколько их уже исправно и ждет наладки. Классификация СМО далеко не ограничивается приведенными разновидностями, но этого достаточно.2. Системы массового обслуживания с ожиданием 2.1 Одноканальная СМО с ожиданием Рассмотрим простейшую СМО с ожиданием — одноканальную систему (n - 1), в которую поступает поток заявок с интенсивностью ; интенсивность обслуживания (т.е. в среднем непрерывно ...
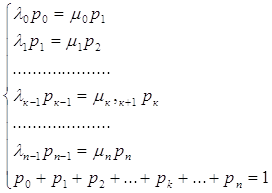
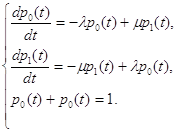
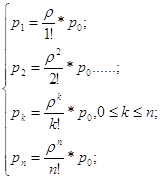
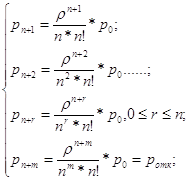
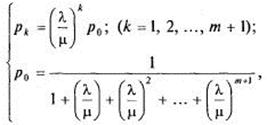
0 комментариев