Навигация
Схема Горнера и теорема Безу
21267
знаков
1
таблица
0
изображений
4. Схема Горнера и теорема Безу.
В кольце многочленов деление в обычном смысле слова, как правило, невозможно. Например, в кольце 
многочлен x2 нельзя разделить на x + 1, т.е. не существует такого многочлена g(x), что x2 = g(x)(x + 1) (если бы такой многочлен существовал, то при x = -1 мы получили бы невозможное равенство 
).
Если для полиномов f(x) и g(x) из K[x] существует такой полином 
, что f(x) = g(x)h(x), то говорят, что полином f(x) делится на полином g(x). Наша ближайшая задача заключается в выяснении вопроса о делимости 
на линейный двучлен x - c при 
.
Прежде всего установим, что всегда осуществимо так называемое деление с остатком: 
при 
. Здесь полином h(x) называется неполным частным, а r - остатком.
Теорема 2. Пусть 
и . Найдутся полином и элемент такие, что . При этом 
.
Доказательство. Естественно искать h(x) в форме 
. Сравнение коэффициентов многочлена в левой части равенства 
= =
с коэффициентами многочлена, полученного после раскрытия скобок и приведения подобных, в правой части этого равенства приводит к цепочке равенств
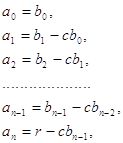
откуда последовательно определяют коэффициенты h(x) и остаток r:
(8)
Равенство непосредственно следует из равенства после подстановки в последнее вместо x элемент c.
Теорема доказана. Кроме того, получен очень удобный способ вычисления коэффициентов h(x) и остатка r. Этот способ носит название схемы Горнера. Вычисления удобно располагать в виде таблицы:
| a0 | a1 | a2 | ... | an-1 | an | |
| c | b0 | b1 | b2 | ... | bn-1 | c |
Элементы нижней строки вычисляются последовательно по формулам (8): b0 = a0, a каждый последующий элемент равен сумме элемента, находящегося над ним, и предыдущего элемента нижней строки, умноженного на x0.
Элемент c кольца K называется корнем полинома f(x), если 
.
Следствие (теорема Безу). Многочлен f(x) делится на 
в кольце K[x]
тогда и только тогда, когда c - его корень.
Доказательство. Пусть f(x) делится на , т.е. 
. Тогда .
Пусть . Тогда в равенстве будет 
, т.е. . Следствие полностью доказано.
Теорема 3. Число корней ненулевого многочлена не превосходит его степени.
Доказательство. Докажем это утверждение с помощью индукции по степени многочлена. Многочлен нулевой степени вообще не имеет корней, так что для него утверждение теоремы справедливо. Предположим теперь, что утверждение теоремы справедливо для всех многочленов степени 
, и докажем его для любого многочлена f(x) степени n. Предположим, рассуждая от противного, что x1, x2, ..., xm - корни многочлена f(x), причем 
. По теореме Безу, f(x) делится на 
, т.е. 
, где g(x) - некоторый многочлен степени . Элементы x2, ..., xm кольца K являются корнями многочлена g(x). В самом деле, при 
имеем: 
. Так как 
, а кольцо K не имеет делителей нуля, то 
. Таким образом, многочлен g(x) имеет не менее чем 
корней, что противоречит предположению индукции, поскольку 
. Теорема доказана.
Следствие. Многочлен степени не выше n однозначно определяется своими значениями в 
точках.
Иначе говоря, существует не более одного многочлена степени не выше n, принимающего в данных (различных) точках 
данные значения y1, y2, ..., yn+1.
Доказательство. Предположим, что f(x), g(x) - два многочлена степени не выше n, принимающие одинаковые значения в точках . Рассмотрим многочлен 
. Степень этого многочлена также не выше, чем n. Так как 
, то 
при 
, т.е. - корни многочлена h(x). Согласно теореме 3 h(x) = 0, т.е. f(x) = g(x).
Теорема 4. Если кольцо K бесконечно, то равенство функций, определяемых двумя многочленами из кольца K[x], влечет за собой равенство самих многочленов.
Доказательство. Пусть многочлены 
определяют одинаковые функции. Это означает, что 
для любого 
. Обозначим через n наивысшую из степеней многочленов f(x), g(x). Так как кольцо K бесконечно, то в нем найдутся различных элементов . Согласно нашему предположению, многочлены f(x) и g(x) принимают одинаковые значения в каждой из точек (как и вообще в любой точке). Следствие теоремы 3 позволяет сделать отсюда вывод, что 
.
Для конечного кольца K утверждение теоремы 4 неверно. Однако при некоторых дополнительных предположениях и в этом случае оказывается возможным из равенства функций, определяемых двумя многочленами, сделать вывод о равенстве самих многочленов.
Похожие работы
... об остатках (КТО). Теорема. Пусть – попарно взаимно простые числа, = , , , …, подобраны так, что 1, = , . Тогда решение системы , , будет иметь вид: . Эта теорема лежит в основе метода ортогональных базисов при переводе из системы остаточных классов в позиционную систему счисления. Пусть основания системы остаточных классов ; = = – объем диапазона системы. С выбором системы определяются ее ...
... 4. Бинарные отношения. Математика как наука отражает мир взаимодействующих простых и сложных объектов (вещей, явлений, процессов). Абстрагируясь от реальности, математика рассматривает унарные, бинарные и другие отношения. В вопросе требуется рассмотреть бинарные отношения, их свойства и особо обратить внимание на отношение эквивалентности, заданного на одном множестве. Рассмотрим ...
... -x * y. Полем называется такое ассоциативное коммутативное кольцо с единицей k, в котором всякий ненулевой элемент обратим: . Таким образом, по определению в поле отсутствуют делители нуля. Кольцом называется множество с двумя алгебраическими операциями R (+, *), если: 0. Обратимыми называют те элементы кольца R, которые имеют обратные относительно операции умножения, множество R в данном случае ...
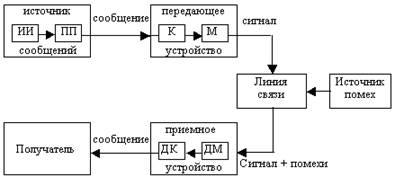
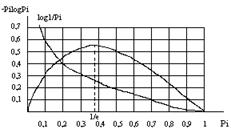
... , работавших в области электротехники, заинтересовалась возможностью создания технологии хранения данных, обеспечивающей более экономное расходование пространства. Одним из них был Клод Элвуд Шеннон, основоположник современной теории информации. Из разработок того времени позже практическое применение нашли алгоритмы сжатия Хаффмана и Шеннона-Фано. А в 1977 г. математики Якоб Зив и Абрахам Лемпел ...
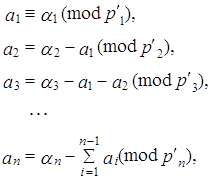
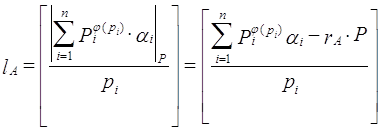
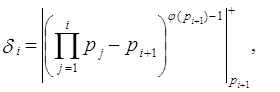
0 комментариев