Навигация
3.1. Постановка L-задачи
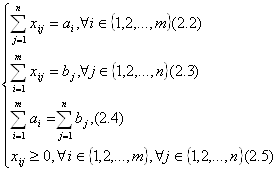
Вспомогательная задача для нахождения начального опорного плана задачи (2.12) - (2.13) в канонической форме состоит в следующем.
Требуется обратить в максимум
![]()
при условиях
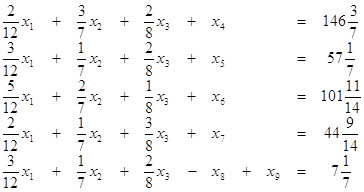
![]() , где
, где ![]() .
.
рассматривая в качестве исходного опорного плана план
Здесь добавление только одной дополнительной переменной ![]() (вместо пяти) обусловлено тем, что исходная задача уже содержит четыре единичных вектора условий А4, А5, А6, А7.
(вместо пяти) обусловлено тем, что исходная задача уже содержит четыре единичных вектора условий А4, А5, А6, А7.
3.2. Решение L-задачи
Решение L-задачи будем проводить в соответствии с первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4). Составим таблицу, соответствующую исходному опорному плану (0-й итерации).
Т.к. Б0 = ![]() - базис, соответствующий известному опорному плану
- базис, соответствующий известному опорному плану![]() , является единичной матрицей, то коэффициенты разложения векторов Аj по базису Б0
, является единичной матрицей, то коэффициенты разложения векторов Аj по базису Б0
![]() .
.
Значение линейной формы ![]() и оценки
и оценки ![]() для заполнения (m+1)-й строки таблицы определяются следующими соотношениями:
для заполнения (m+1)-й строки таблицы определяются следующими соотношениями:
![]() ,
,
![]() .
.
Отсюда получим:
![]() ;
;
![]() ;
;
![]() ;
;
…
![]() .
.
Весь процесс решения задачи приведен в табл. 3.2.1, которая состоит из 2 частей, отвечающих 0-й (исходная таблица) и 1-й итерациям.
Заполняем таблицу 0-й итерации.
Среди оценок ![]() имеются отрицательные. Значит, исходный опорный план не является оптимальным. Перейдем к новому базису. В базис будет введен вектор А1 с наименьшей оценкой
имеются отрицательные. Значит, исходный опорный план не является оптимальным. Перейдем к новому базису. В базис будет введен вектор А1 с наименьшей оценкой ![]() . Значения t вычисляются для всех позиций столбца t (т.к. все элементы разрешающего столбца положительны). Наименьший элемент
. Значения t вычисляются для всех позиций столбца t (т.к. все элементы разрешающего столбца положительны). Наименьший элемент ![]() достигается на пятой позиции базиса. Значит, пятая строка является разрешающей строкой, и вектор А9 подлежит исключению из базиса.
достигается на пятой позиции базиса. Значит, пятая строка является разрешающей строкой, и вектор А9 подлежит исключению из базиса.
Составим таблицу, отвечающую первой итерации.
В столбце Бх, в пятой позиции базиса место вектора А9 занимает вектор А1. Соответствующий ему коэффициент линейной формы С41 = 0 помещаем в столбец Сх. Главная часть таблицы 1 заполняется по данным таблицы 0 в соответствии с рекуррентными формулами. Так как все ![]() , то опорный план
, то опорный план ![]() является решением L-задачи. Наибольшее значение линейной формы равно
является решением L-задачи. Наибольшее значение линейной формы равно ![]() .
.
Таблица 3.2.1

3.3. Формирование начального опорного плана исходной задачи линейного программирования из оптимального плана L-задачи
Поскольку ![]() , где
, где ![]()
![]() - оптимальный опорный план L-задачи, то
- оптимальный опорный план L-задачи, то ![]()
![]() является начальным опорным планом исходной задачи (2.12) - (2.13).
является начальным опорным планом исходной задачи (2.12) - (2.13).
4. Решение исходной задачи I алгоритмом симплекс-метода
Описание I алгоритма
Симплекс-метод позволяет, отправляясь от некоторого исходного опорного плана и постепенно улучшая его, получить через конечное число итераций оптимальный план или убедиться в неразрешимости задачи. Каждой итерации соответствует переход от одной таблицы алгоритма к следующей. Таблица, отвечающая опорному плану в ν-й итерации имеет вид табл. 4.1.
Таблица 4.1
| C |
| … |
| … |
| … |
| ||||
| N |
|
| B |
| … |
| … |
| … |
| t |
| 1 |
|
|
|
| … |
| … |
| … |
| |
|
|
|
|
|
|
|
|
|
|
|
| |
| l |
|
|
|
| … |
| … |
| … |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| m |
|
|
|
| … |
| … |
| … |
| |
| m+1 | – | – |
|
| … |
| … |
| … |
| – |
Заполнение таблицы, соответствующей исходному опорному плану (0-й итерации). Пусть ![]() некоторый опорный план задачи (2.1) - (2.3) с базисом
некоторый опорный план задачи (2.1) - (2.3) с базисом ![]() . Тогда
. Тогда ![]() – базисные компоненты, а
– базисные компоненты, а ![]() – небазисные компоненты.
– небазисные компоненты.
Вычисляем коэффициенты разложения векторов Аj по базису Б0
![]() (в случае, если Б0 является единичной матрицей,
(в случае, если Б0 является единичной матрицей, ![]() )
)
и находим оценки ![]() . Далее определяем значение линейной формы
. Далее определяем значение линейной формы
![]()
Полученные результаты записываем в таблицу 4.1.
В первом столбце N таблицы указываются номера строк. Номера первых m строк совпадают с номерами позиций базиса. Во втором столбце Сх записываются коэффициенты ![]() линейной формы при базисных переменных. Столбец Бх содержит векторы базиса
линейной формы при базисных переменных. Столбец Бх содержит векторы базиса ![]() . В столбце В записываются базисные переменные
. В столбце В записываются базисные переменные ![]() опорного плана. Столбцы
опорного плана. Столбцы ![]() содержат коэффициенты
содержат коэффициенты ![]() разложения соответствующих векторов условий
разложения соответствующих векторов условий ![]() по векторам базиса. Все вышесказанное относится только к первым m строкам таблицы. Последняя (m+1)-я строка таблицы заполняется последовательно значением линейной формы F и оценками
по векторам базиса. Все вышесказанное относится только к первым m строкам таблицы. Последняя (m+1)-я строка таблицы заполняется последовательно значением линейной формы F и оценками ![]() . Позиции таблицы, которые не должны заполняться, прочеркиваются.
. Позиции таблицы, которые не должны заполняться, прочеркиваются.
В результате заполнена таблица 0-й итерации кроме столбца t.
Столбцы В, А1,…, An (все m+1 позиций) будем называть главной частью таблицы.
Порядок вычислений в отдельной итерации. Пусть ν-я итерация закончена. В результате заполнена таблица ν за исключением последнего столбца t.
Каждая итерация состоит из двух этапов.
I этап: проверка исследуемого опорного плана на оптимальность.
Просматривается (m+1)-я строка таблицы ν. Если все ![]() , то опорный план, полученный после ν-й итерации, является оптимальным (случай 1), завершаем решение задачи. Пусть теперь имеются отрицательные оценки. Проверяем знаки элементов
, то опорный план, полученный после ν-й итерации, является оптимальным (случай 1), завершаем решение задачи. Пусть теперь имеются отрицательные оценки. Проверяем знаки элементов ![]() столбцов
столбцов ![]() с
с ![]() . Наличие по крайней мере одного столбца
. Наличие по крайней мере одного столбца ![]() , для которого
, для которого ![]() и все
и все ![]() , свидетельствует о неразрешимости задачи (случай 2). Установив это, прекращаем вычисления.
, свидетельствует о неразрешимости задачи (случай 2). Установив это, прекращаем вычисления.
Если в каждом столбце ![]() , для которого
, для которого ![]() , содержится хотя бы один положительный коэффициент
, содержится хотя бы один положительный коэффициент ![]() , то опорный план является неоптимальным (случай 3). Переходим ко II этапу.
, то опорный план является неоптимальным (случай 3). Переходим ко II этапу.
II этап: построение нового опорного плана с большим значением линейной формы.
Определяется вектор Ak, который должен быть введен в базис, из следующего условия
![]() .
.
После этого заполняется последний столбец таблицы ν – столбец t. В него записываются отношения базисных переменных ![]() (элементы столбца В) к соответствующим составляющим
(элементы столбца В) к соответствующим составляющим ![]() (элементы столбца Ak). Т.о. заполняются только те позиции, для которых
(элементы столбца Ak). Т.о. заполняются только те позиции, для которых ![]() . Если
. Если ![]() , то в позиции i столбца t записывается
, то в позиции i столбца t записывается ![]() . Вектор базиса
. Вектор базиса ![]() , на котором достигается t0,
, на котором достигается t0,
 ,
,
подлежит исключению из базиса (если t0 достигается на нескольких векторах, то из базиса исключается любой из них).
Столбец Ak, отвечающий вектору, вводимому в базис, и l-я строка, соответствующая вектору ![]() , исключаемому из базиса, называется соответственно разрешающим столбцом и разрешающей строкой. Элемент
, исключаемому из базиса, называется соответственно разрешающим столбцом и разрешающей строкой. Элемент ![]() , расположенный на пересечении разрешающего столбца и разрешающей строки, называется разрешающим элементом.
, расположенный на пересечении разрешающего столбца и разрешающей строки, называется разрешающим элементом.
После выделения разрешающего элемента заполняется (ν+1)-я таблица. В l-е позиции столбцов Бх, Сх вносятся соответственно Ак, Ск, которые в (ν+1)-й таблице обозначаются как ![]() ,
, ![]() . В остальные позиции столбцов Бх, Сх вносятся те же параметры, что и в таблице ν.
. В остальные позиции столбцов Бх, Сх вносятся те же параметры, что и в таблице ν.
Далее заполняется главная часть (ν+1)-й таблицы. Прежде всего происходит заполнение ее l-й строки в соответствии с рекуррентной формулой
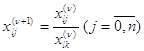 .
.
Рекуррентная формула для заполнения i-й строки (ν+1)-й таблицы имеет вид
![]() .
.
Здесь
![]() .
.
Заполнение главной части (ν+1)-й таблицы завершает (ν+1)-ю итерацию. Последующие итерации проводятся аналогично. Вычисления продолжаются до тех пор, пока не будет получен оптимальный план либо будет установлено, что исследуемая задача неразрешима.
Решение исходной задачи
Весь процесс решения исходной задачи (2.12) - (2.13) приведен в табл. 4.2.
Заполнение таблицы, отвечающей 0-й итерации, происходит на основе табл. 3.2.1 (см. итерацию 1) следующим образом. Главная часть таблицы 0-й итерации исходной задачи (за исключением (m+1)-й строки) полностью повторяет главную часть таблицы заключительной итерации L-задачи без столбца А9. Также без изменений остается столбец базисных векторов Бх. Строка С коэффициентов линейной формы исходной задачи и столбец Сх коэффициентов при базисных переменных заполняются исходя из (2.12). С учетом новых коэффициентов С пересчитываются значение линейной формы F и оценки ![]() .
.
Заполнение таблиц, отвечающих последующим итерациям, происходит в соответствии с описанным выше первым алгоритмом.
Таблица 4.2
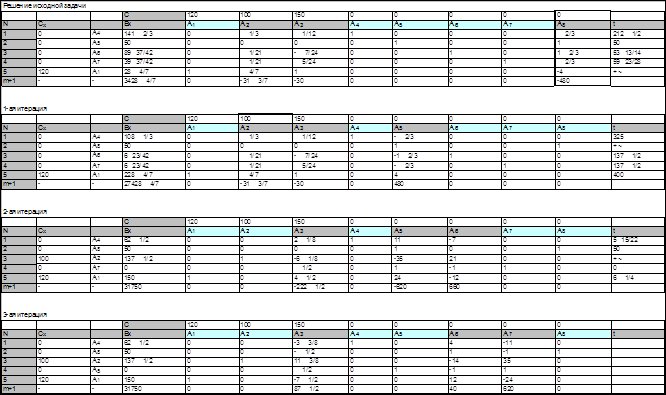
Решение исходной задачи (2.12) - (2.13) получено за 3 итерации. Оптимальный план ее равен ![]() и
и ![]() .
.
Найденное решение ![]() задачи в канонической форме (2.12) - (2.13) соответствует решению
задачи в канонической форме (2.12) - (2.13) соответствует решению ![]() (4.1) общей задачи линейного программирования (2.9) - (2.11), записанной для новых переменных
(4.1) общей задачи линейного программирования (2.9) - (2.11), записанной для новых переменных ![]() . Для общей задачи из (2.9) следует, что
. Для общей задачи из (2.9) следует, что ![]() (4.2).
(4.2).
Вернемся к задаче (1.2.1), (1.2.2) со старыми переменными ![]() . Учитывая (4.1) и (4.2) из (2.7) и (2.8) получим
. Учитывая (4.1) и (4.2) из (2.7) и (2.8) получим
 (4.3)
(4.3)
и
![]() .
(4.4)
.
(4.4)
Таким образом, для получения максимальной цены (142750 руб.) всей продукции необходимо произвести:
450 тыс.л. бензина А из полуфабрикатов в следующих количествах:
Алкитата ![]() тыс.л.
тыс.л.
Крекинг-бензина ![]() тыс.л.
тыс.л.
Бензина прямой перегонки ![]() тыс.л.
тыс.л.
Изопентона ![]() тыс.л.
тыс.л.
![]() тыс.л. бензина В из полуфабрикатов в следующих количествах:
тыс.л. бензина В из полуфабрикатов в следующих количествах:
Алкитата ![]() тыс.л.
тыс.л.
Крекинг-бензина ![]() тыс.л.
тыс.л.
Бензина прямой перегонки ![]() тыс.л.
тыс.л.
Изопентона ![]() тыс.л.
тыс.л.
300 тыс.л. бензина В из полуфабрикатов в следующих количествах:
Алкитата ![]() тыс.л.
тыс.л.
Крекинг-бензина ![]() тыс.л.
тыс.л.
Бензина прямой перегонки ![]() тыс.л.
тыс.л.
Изопентона ![]() тыс.л.
тыс.л.
Похожие работы
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... - метод для решения задач линейного программирования. Задачи курсовой заботы: 1. привести теоретический материал; 2. на примерах рассмотреть симплекс метод; 3. представить данную курсовую работу в виде презентации. Математическое программирование Математическое программирование занимается изучение экстремальных задач и поиском методов их решения. Задачи ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
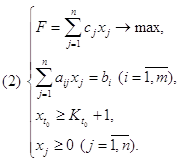


0 комментариев