Навигация
Методы построения маршрутных матриц СеМО
3. Методы построения маршрутных матриц СеМО.
3.1. Общее решение.
Задача построения маршрутной матрицы виртуальной СеМО может быть решена следующим образом:
Пусть дана концептуальная эталонная виртуальная СеМО , состоящая из L СМО. Для которой определены вектор , орграф , матрица смежности , множество , множество коэффициентов обмена.
Необходимо сформулировать маршрутную матрицу ,т.е. найти L2 неизвестных , .
Из уравнений (22) - (23) получили значения неизвестных ,где Х определяется (14).
В результате получили систему линейных алгебраических уравнений (18) - (20) от Х неизвестных (индекс сверху - порядковый номер неизвестной).
Решая систему методом Гаусса, получим один из трех возможных вариантов:
Система неразрешима. В этом случае сформировать маршрутную матрицу , а следовательно и виртуальную эталонную СеМО невозможно.
Система разрешима однозначно. В этом случае необходимо проверить, удовлетворяют ли полученные значения неравенствам (23). Если неравенства выполняются, то полученное решение дает значения оставшихся Х неизвестных , т. о. заканчивается формирование маршрутной матрицы . Если (23) не выполняется, то сформировать
невозможно.
Система разрешима неоднозначно. Общее решение системы (18) - - (20) фактически определяет бесконечное множество подобных матриц для конкретной концептуальной СеМО. Задание конкретных значений свободных переменных определяет конкретную маршрутную матрицу для такой СеМО. Очевидно, что это конкретное решение должно удовлетворять ограничениям (23).
Пусть первые m переменных - свободные, тогда если , то остальные , можно записать как . Т. е. остальные (Х-m) переменных могут быть линейно выражены через . Подставляя полученные выражения в неравенства
(24)
получим систему неравенств:
(25)
Эта система неравенств образует так называемое многогранное множество в m - мерном пространстве. Если это множество не пусто, то, так как оно ограничено, оно является выпуклым многогранником. Точка называется вершиной выпуклого многогранника в , если она является допустимой и представляет собой точку пересечения m линейно независимых гиперплоскостей. (Каждое линейное уравнение задает гиперплоскость, каждому линейному неравенству из (25) сопоставляется ограниченное гиперплоскостью полупространство; гиперплоскость получают, заменяя знак неравенства на знак равенства.) Вершина вырожденная, если она является точкой пересечения более чем m гиперплоскостей.
Вершину нельзя представить в виде выпуклой линейной комбинации двух других точек допустимой области для всех допустимых точек ( ). Всякое многогранное множество имеет конечное число вершин. Если допустимая область образована n неравенствами и m уравнениями, то она может иметь самое большее вершин. Т. к. допустимая область в данном случае является выпуклым многогранником, то каждая допустимая точка имеет по меньшей мере одно представление:
(26),
где - вершины многогранника; .
Таким образом, если мы найдем все вершины многогранника (если они существуют. В противном случае решения не существует), то мы получим общее решение задачи формирования матрицы .
где - допустимая точка, найденная по формуле (26). Получим оставшиеся Х неизвестных и завершим построение маршрутной матрицы.
3.2. Пример нахождения общего решения.
Дана концептуальная эталонная виртуальная СеМО , с L=5, для которой определены концептуальный вектор , орграф , матрица смежностей .
Множество .
Из уравнений (21), (22) получим значения 15 неизвестных маршрутных вероятностей из 25. Оставшиеся неизвестные занумеруем ,
получим:
Рассмотрим систему линейных уравнений (18), (19), (17). Применяя к ней алгоритм Гаусса получим:
система совместна.
решение неоднозначно 10-8=2 неизвестных могут быть выбраны произвольно.
Решаем систему и получаем:
(*)
Подставим результаты в (25). Получим систему типа (26):
(27)
Эта система неравенств образует многогранное множество, изображенное на рис. 1.
Любая пара принадлежащая допустимой области удовлетворяет системе (27).
Многограннику имеет 5 вершин:
Любая точка допустимого множества имеет представление , где - вершины, , , . Пусть, например, , тогда
. Подставим значения и в (*), получим
Рисунок 1.
3.3. Метод формирования маршрутной матрицы виртуальной СеМО.
Задача построения виртуальной СеМО может быть сведена к задаче нелинейного программирования.
Пусть задана концептуальная виртуальная СеМО , для которой задан концептуальный вектор , орграф , матрица смежностей , множество .
Задачей нелинейного программирования общего вида называется задача: Найти
(2.1)
при ограничениях
(2.2)
Введем в рассмотрение функцию ; очевидно, что если отыщется такая, что ,то есть искомая маршрутная матрица. Т. о. мы получили задачу:
(2.3)
при ограничениях
(2.4)
Задача (2.3) - (2.4) является задачей нелинейного программирования. Ее можно отнести к задачам квадратичного программирования - класс задач для которых целевая функция квадратична, а все ограничения линейны.
Решая задачу (2.3) - (2.4) одним из методов, рассмотренных в [3-5] можно получить один из результатов:
, где . В этом случае сформировать маршрутную матрицу невозможно.
. В этом случае есть искомая маршрутная матрица виртуальной СеМО.
Для решения ЗНП разработан ряд методов, позволяющих, отправляясь от некоторого начального решения, получать последовательно значения, которые находятся все ближе к искомой точке максимума (минимума). Группа методов, основанных на вычислении и сравнении значений целевой функции в ряде точек перед следующим шагом, называется поисковыми методами оптимизации.
В задаче можно представить целевую функцию как гиперповерхность. Максимальное значение достигается в вершине самого высокого холма. Поиск экстремума начинают с любой удобной точки, причем двигаются в направлении наискорейшего подъема, пока не достигают либо вершины, либо границы. При достижении границы необходимо исключить перемещение за пределы ограничений. При достижении вершины, которая встретилась в направлении наискорейшего подъема поворачивают во вновь выбранном направлении наискорейшего подъема. Таким образом достигают точки, где движение в любом направлении приводит к спуску. В этом случае утверждают, что найден по крайней мере локальный экстремум.
На практике, при реализации этого метода возникают две трудности. Во-первых, это относительная малая скорость сходимости. Для преодоления этого служат методы нахождения более эффективных направлений, чем направление наискорейшего подъема. Вторая трудность состоит в том, что этот метод позволяет обнаружить локальные максимумы, но не дает гарантии достижения абсолютного (глобального) экстремума. Чтобы преодолеть эту трудность обычно начинают поиск из различных точек, и, если вычисления сходятся к разным вершинам, то выбирают наиболее высокую из них. Также можно использовать метод, известный под названием “метод тяжелого шарика”, при котором движение точки напоминает движение тяжелого шарика по бугристой поверхности. Рассмотрим некоторые из методов поисковой оптимизации.
Похожие работы
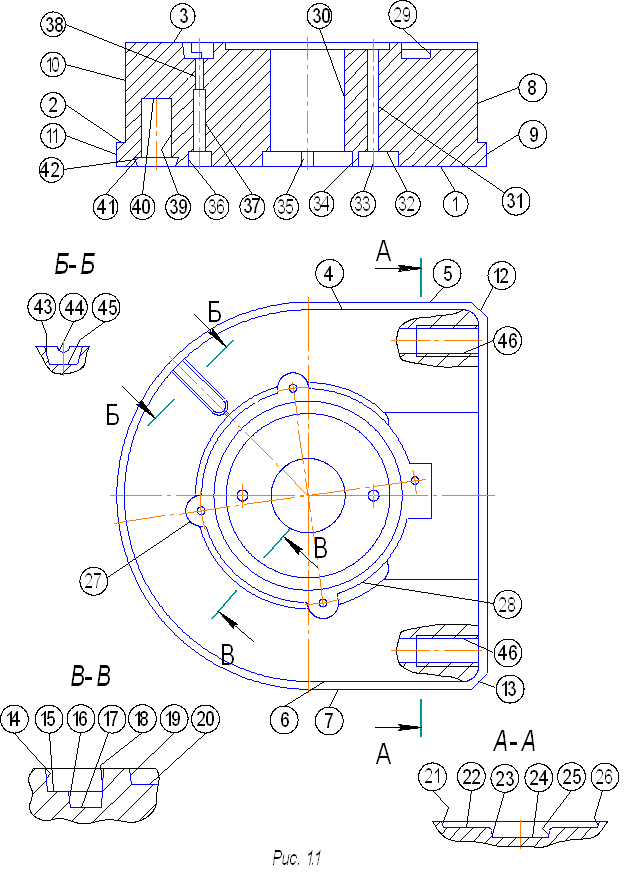
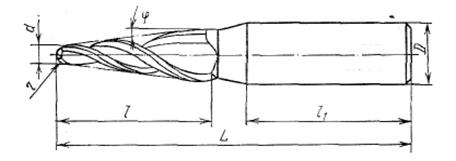
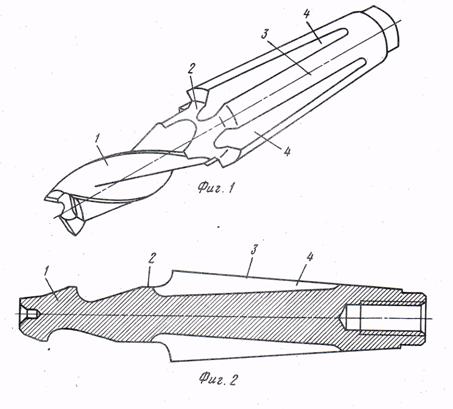
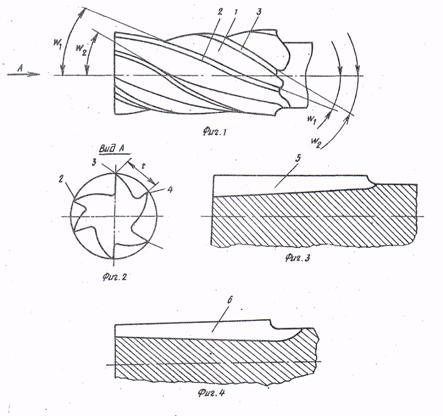
... 7 0,8 Сверление, зенкерование, развертывание. 34 12 12,5 Растачивание 36,37,46 11 12,5 Сверление Данные методы реализованы при разработке технологического маршрута изготовления матрицы. Разработка технологического маршрута изготовления матрицы При разработке маршрута в среднесерийном производстве придерживались следующих правил: 1.Технологические операции разрабатывали по принципу ...
... со строгими методами оптимизации образуют жесткую структуру, изменения которой осуществляются разработчиками или специальными лицами, администрирующими информационную компоненту и сопровождающими систему автоматизированного проектирования. Они не являются специалистами в данной предметной области. ЛОГИЧЕСКИЕ МЕТОДЫ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ Предварительно остановимся на изложении некоторых понятий ...
0 комментариев