Навигация
Этьен Безу–
французский математик, член Парижской Академии Наук( с 1758 года ), родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года.
С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.
Основные работы Этьена Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений. В теории решения систем линейных уравнений он содействовал возникновению теории определителей , развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную К. Маклореном ) о том , что две кривые порядка m и n пересекаются не более чем в mn точках. Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный“Курс математики “, написанный им в 1764-69 годах. Безу развил метод неопределённых множителей, в элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе . Часть трудов Безу посвящена внешней баллистике. Именем учёного названа одна из основных теорем алгебры.
Теорема Безу.
Остаток от деления полинома Pn(x)
на двучлен (x-a) равен значению
этого полинома при x = a.
Пусть :Pn(x) – данный многочлен степени n ,
двучлен (x-a) - его делитель,
Qn-1(x) – частное от деления Pn(x) на x-a (многочлен степени n-1 ) ,
R – остаток от деления ( R не содержит переменной x как делитель первой степени относительно x ).
Доказательство :
Согласно правилу деления многочленов с остатком можно записать :
Pn (x) = (x-a)Qn-1(x) + R .
Отсюда при x = a :
Pn (a) = (a-a)Qn-1 (a) + R =0*Qn-1(a)+R=
=0+R=R .
Значит , R = Pn (a) , т.е. остаток от деления полинома на (x-a) равен значению этого
полинома при x=a , что и требовалось доказать .
Следствия из теоремы .
Следствие 1 :
Остаток от деления полинома Pn (x)
на двучлен ax+b равен значению
этого полинома при x = -b/a ,
т. е. R=Pn (-b/a) .
Доказательство :
Согласно правилу деления многочленов :
Pn (x)= (ax + b)* Qn-1 (x) + R .
При x= -b/a :
Pn (-b/a) = (a(-b/a) + b)Qn-1(-b/a) + R = R. Значит , R = Pn (-b/a) , что и требовалось доказать.
Следствие 2:
Если число a является корнем
многочлена P (x) , то этот
многочлен делится на (x-a) без
остатка .
Доказательство :
По теореме Безу остаток от деления многочлена P (x) на x-a равен P (a) , а по условию a является корнем P (x) , а это значит , что P (a) = 0 , что и требовалось доказать .
Из данного следствия теоремы Безу видно , что задача решения уравнения P (x) = 0 равносильна задаче выделения делителей многочлена P , имеющих первую степень ( линейных делителей ) .
Следствие 3 :
Если многочлен P (x) имеет
попарно различные корни
a1 , a2 , … , an , то он делится на
произведение (x-a1) … (x-an)
без остатка .
Доказательство :
Проведём доказательство с помощью математической индукции по числу корней . При n=1 утверждение доказано в следствии 2 . Пусть оно уже доказано для случая , когда число корней равно k , это значит , что P(x) делится без остатка на (x-a1)(x-a2) … (x-ak) , где
a1 , a2 , … , ak - его корни .
Пусть P(x) имеет k+1 попарно различных корней .По предположению индукции a1 , a2 , ak , … , ak+1 являются корнями многочлена, а , значит, многочлен делится на произедение (x-a1) … (x-ak) , откуда выходит , что
P(x) = (x-a1) … (x-ak)Q(x).
При этом ak+1 – корень многочлена P(x) , т. е. P(ak+1) = 0 .
Значит , подставляя вместо x ak+1 , получаем верное равенство :
P(ak+1) = (ak+1-a1) … (ak+1-ak)Q(ak+1) =
=0 .
Но ak+1 отлично от чисел a1 , … , ak , и потому ни одно из чисел ak+1-a1 , … , ak+1-ak не равно 0 . Следовательно , нулю равно Q(ak+1) , т. е. ak+1 – корень многочлена Q(x) . А из следствия 2 выходит , что Q(x) делится на x-ak+1 без остатка .
Q(x) = (x-ak+1)Q1(x) , и потому
P(x) = (x-a1) … (x-ak)Q(x) =
=(x-a1) … (x-ak)(x-ak+1)Q1(x) .
Это и означает , что P(x) делится на (x-a1) … (x-ak+1) без остатка .
Итак, доказано , что теорема верна при k =1 , а из её справедливости при n = k вытекает , что она верна и при n = k+1. Таким образом, теорема верна при любом числе корней , что и требовалось доказать .
Следствие 4 :
Многочлен степени n имеет не более
n различных корней .
Доказательство :
Воспользуемся методом от противного: если бы многочлен Pn(x) степени n имел бы более n корней - n+k (a1 , a2 , … , an+k - его корни ) , тогда бы по ранее доказанному следствию 3 он
бы делился на произведение (x-a1) … (x-an+k) , имеющее степень n+k , что невозможно .
Мы пришли к противоречию , значит наше предположение неверно и многочлен степени n не может иметь более , чем n корней , что и требовалось доказать .
Следствие 5 :
Для любого многочлена P(x)
и числа a разность
(P(x)-P(a)) делится без
остатка на двучлен (x-a) .
Доказательство :
Пусть P(x) – данный многочлен степени n , a - любое число .
Многочлен Pn(x) можно представить в виде : Pn(x)=(x-a)Qn-1(x)+R ,
где Qn-1(x) – многочлен , частное при делении Pn(x) на (x-a) ,
R – остаток от деления Pn(x) на (x-a) .
Причём по теореме Безу :
R = Pn(a) , т.е.
Pn(x)=(x-a)Qn-1(x)+Pn(a) .
Отсюда
Pn(x) - Pn(a) = (x-a)Qn-1(x) ,
а это и означает делимость без остатка ( Pn(x) – Pn(a) )
на (x-a) , что и требовалось доказать .
Следствие 6 :
Число a является корнем
многочлена P(x) степени
не ниже первой тогда и
только тогда , когда
P(x) делится на (x-a)
без остатка .
Доказательство :
Чтобы доказать данную теорему требуется рассмотреть необходимость и достаточность сформулированного условия .
1.Необходимость .
Пусть a – корень многочлена P(x) , тогда по следствию 2 P(x) делится на (x-a) без остатка .
Таким образом делимость P(x) на (x-a) является необходимым условием для того , чтобы a являлось корнем P(x) , т.к. является следствием из этого .
2.Достаточность .
Пусть многочлен P(x) делится без остатка на (x-a),
тогда R = 0 , где R – остаток от деления P(x) на (x-a) , но по теореме Безу R = P(a) , откуда выходит , что P(a) = 0 , а это означает , что a является корнем P(x) .
Таким образом делимость P(x) на (x-a) является и достаточным условием для того , чтобы a являлось корнем P(x) .
Делимость P(x) на (x-a) является необходимым и достаточным условием для того, чтобы a являлось корнем P(x) , что и требовалось доказать .
Следствие 7(авторское):
Многочлен , не имеющийй действи-
тельных корней , в разложении
на множители линейных множителей
не содержит .
Доказательство :
Воспользуемся методом от противного: предполо-жим , что не имеющий корней многочлен P(x) при разложении на множители содержит линейный множитель (x – a):
P(x) = (x – a)Q(x),
тогда бы он делился на (x – a) , но по следствию 6 a являлось бы корнем P(x) , а по условию он корней не содержит . Мы пришли к противоречию , значит наше предположение неверно и многочлен ,
не имеющий действительных корней , в разложении на множители линейных множителей не содержит , что и требовалось доказать .
На основании теоремы Безу и следствия 5 можно доказать следующие утверждения:
1. Разность одинаковых натуральных степеней на разность их оснований делится без остатка :
Пусть P(x) = xn , P(a) = an ,
тогда xn – an – разность одинаковых натуральных степеней .
По следствию 5
P(x) - P(a) = xn – an = (x – a)Q(x) ,
а это значит , что
(xn–an)/(x–a)=Q(x), т.е. разность одинаковых натуральных степеней на разность их оснований делится без остатка , что и требовалось доказать .
Итак
(xn – an)/(x – a) = xn-1 + axn-2 + a2xn-3 + … +an-2x + an-1.
Похожие работы
... (x-a) равен f(a), а по условию a является корнем f(x), а это значит, что f(a)=0, что и требовалось доказать. Из данного следствия теоремы Безу видно, что задача решения уравнения f(x)=0 равносильна задаче выделения делителей многочлена f, имеющих первую степень (линейных делителей). Следствие 3: Если многочлен f(x) имеет попарно различные корни a1, a2 ,… ,an ,то он делится на произведение ...
... которого на один ниже степени многочлена Также данный метод называют понижением степени. Благодаря данному способу можно найти оставшиеся корни многочлена. 2.4. Примеры использования теоремы. Пример. Найти остаток от деления многочлена на . Решение. На основании теоремы Безу подставляем вместо x число -5. Получаем r(x)= В результате мы получили остаток r(x) равный 180. Пример. С ...
... тьюринговых машин. Проблема заключается в следующем как по любому заданному шрифту установить к какому классу относится машина, зашифрованная им: к классу самоприменимых или несамоприменимых. Теорема 2. Проблема распознавания самоприменимости алгоритмически неразрешима. 3). Проблема эквивалентности слов для ассоциативных исчислений. Рассмотрим некоторый алфавит и множество слов в этом алфавите. ...
... f(x) непрерывна в замкнутом круге Е, то она ограничена. Лемма №6. Действительная функция комплексного переменного f(x) непрерывная в замкнутом круге Е достигает своего минимума и максимума. Доказательство основной теоремы. Лемма №1.Надо доказать, что |f(x0+x)-f(x0)|<e. Докажем Лемму №1 сначала для многочлена без свободного члена и при x0=0 ЕслиA=max(|a0 |,|a1|,…,|a n-1|) и (1) то ...
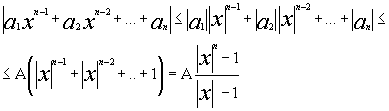
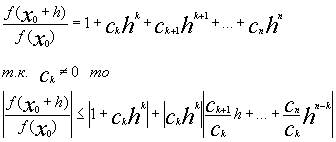
0 комментариев