Навигация
Проверка большого числа на простоту
3.3. Проверка большого числа на простоту
Есть некоторое
отличие в постановках
задач предыдущего
и настоящего
пунктов. Когда
мы строим простое
число ![]() ,
мы обладаем
некоторой
дополнительной
информацией
о нем, возникающей
в процессе
построения.
Например, такой
информацией
является знание
простых делителей
числа
,
мы обладаем
некоторой
дополнительной
информацией
о нем, возникающей
в процессе
построения.
Например, такой
информацией
является знание
простых делителей
числа ![]() .
Эта информация
иногда облегчает
доказательство
простоты
.
Эта информация
иногда облегчает
доказательство
простоты ![]() .
.
В этом пункте
мы предполагаем
лишь, что нам
задано некоторое
число ![]() ,
например, выбранное
случайным
образом на
каком-то промежутке,
и требуется
установить
его простоту,
или доказать,
что оно является
составным. Эту
задачу за
полиномиальное
количество
операций решает
указанный в
п. 3 алгоритм
Миллера. Однако,
справедливость
полученного
с его помощью
утверждения
зависит от
недоказанной
расширенной
гипотезы Римана.
Если число
,
например, выбранное
случайным
образом на
каком-то промежутке,
и требуется
установить
его простоту,
или доказать,
что оно является
составным. Эту
задачу за
полиномиальное
количество
операций решает
указанный в
п. 3 алгоритм
Миллера. Однако,
справедливость
полученного
с его помощью
утверждения
зависит от
недоказанной
расширенной
гипотезы Римана.
Если число ![]() выдержало
испытания
алгоритмом
5 для 100 различных
значений параметра
выдержало
испытания
алгоритмом
5 для 100 различных
значений параметра
![]() ,
то, по-видимому,
можно утверждать,
что оно является
простым с
вероятностью
большей, чем
,
то, по-видимому,
можно утверждать,
что оно является
простым с
вероятностью
большей, чем
![]() .
Эта вероятность
очень близка
к единице, однако
всё же оставляет
некоторую тень
сомнения на
простоте числа
.
Эта вероятность
очень близка
к единице, однако
всё же оставляет
некоторую тень
сомнения на
простоте числа
![]() .
В дальнейшем
в этом пункте
мы будем считать,
что заданное
число
.
В дальнейшем
в этом пункте
мы будем считать,
что заданное
число ![]() является простым,
а нам требуется
лишь доказать
это.
является простым,
а нам требуется
лишь доказать
это.
В настоящее
время известны
детерминированные
алгоритмы
различной
сложности для
доказательства
простоты чисел.
Мы остановимся
подробнее
на одном из
них, предложенном
в 1983 г. в совместной
работе Адлемана.
Померанца и
Рамели. Для
доказательства
простоты или
непростоты
числа ![]() этот алгоритм
требует
этот алгоритм
требует ![]() арифметических
операций. Здесь
арифметических
операций. Здесь
![]() - некоторая
положительная
абсолютная
постоянная.
Функция
- некоторая
положительная
абсолютная
постоянная.
Функция ![]() хоть и медленно,
но всё же возрастает
с ростом
хоть и медленно,
но всё же возрастает
с ростом ![]() ,
поэтому алгоритм
не является
полиномиальным.
Но всё же его
практические
реализации
позволяют
достаточно
быстро тестировать
числа на простоту.
Существенные
усовершенствования
и упрощения
в первоначальный
вариант алгоритма
были внесены
в работах X.
Ленстры и А.
Коена. Мы будем
называть описываемый
ниже алгоритм
алгоритмом
Адлемана - Ленстры.
,
поэтому алгоритм
не является
полиномиальным.
Но всё же его
практические
реализации
позволяют
достаточно
быстро тестировать
числа на простоту.
Существенные
усовершенствования
и упрощения
в первоначальный
вариант алгоритма
были внесены
в работах X.
Ленстры и А.
Коена. Мы будем
называть описываемый
ниже алгоритм
алгоритмом
Адлемана - Ленстры.
В основе
алгоритма лежит
использование
сравнений типа
малой теоремы
Ферма, но в кольцах
целых чисел
круговых полей,
т. е. полей. порождённых
над полем ![]() числами
числами ![]() - корнями из 1.
Пусть
- корнями из 1.
Пусть ![]() - простое нечётное
число и
- простое нечётное
число и ![]() — первообразный
корень по модулю
— первообразный
корень по модулю
![]() ,
т. е. образующий
элемент мультипликативной
группы поля
,
т. е. образующий
элемент мультипликативной
группы поля
![]() ,
которая пиклична.
Для каждого
целого числа
,
которая пиклична.
Для каждого
целого числа
![]() ,
не делящегося
на
,
не делящегося
на ![]() ,
можно определить
его индекс,
,
можно определить
его индекс, ![]() ,
называемый
также дискретным
логарифмом,
с помощью сравнения
,
называемый
также дискретным
логарифмом,
с помощью сравнения
![]() .
Рассмотрим
далее два простых
числа
.
Рассмотрим
далее два простых
числа ![]() ,
,
![]() с условием, что
с условием, что
![]() делится на
делится на ![]() ,
но не делится
на
,
но не делится
на ![]() .
.
Следующая функция, определённая на множестве целых чисел.
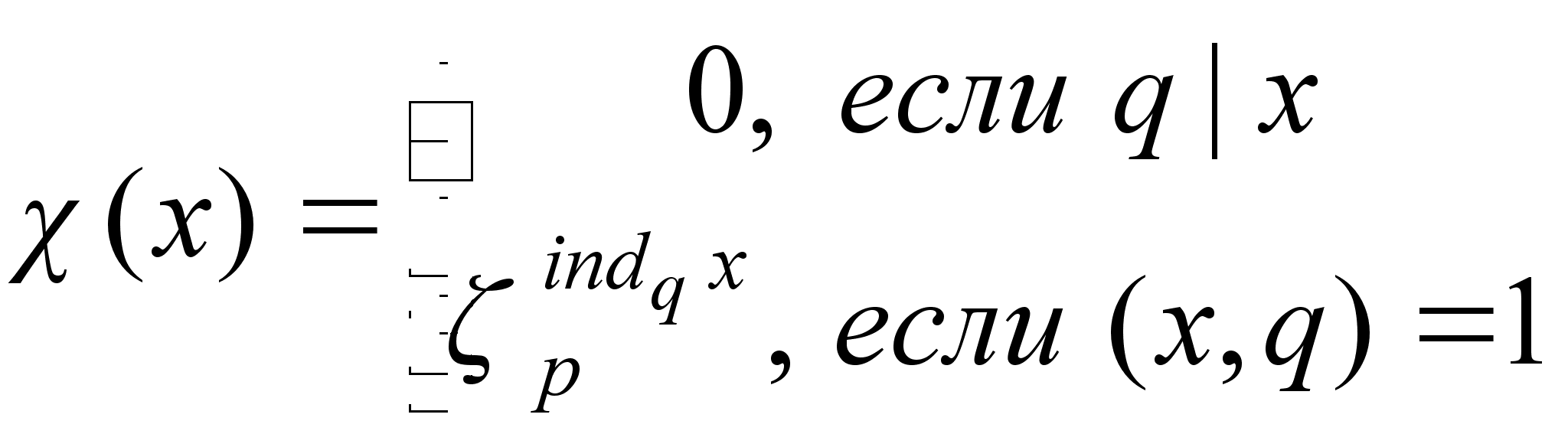
является
характером
по модулю ![]() и порядок этого
характера равен
и порядок этого
характера равен
![]() .
.
Сумма

называется суммой Гаусса. Формулируемая ниже теорема 3 представляет собой аналог малой теоремы Ферма, используемый в алгоритме Адлемана - Ленстры.
Теорема
3. Пусть ![]() - нечетное простое
число,
- нечетное простое
число, ![]() .
Тогда в кольце
.
Тогда в кольце
![]() выполняется
сравнение
выполняется
сравнение
![]() .
.
Если при
каких-либо
числах ![]() сравнение из
теоремы 3 нарушается.
можно утверждать,
что
сравнение из
теоремы 3 нарушается.
можно утверждать,
что ![]() составное
число. В противном
случае, если
сравнение
выполняется,
оно даёт некоторую
информацию
о возможных
простых делителях
числа
составное
число. В противном
случае, если
сравнение
выполняется,
оно даёт некоторую
информацию
о возможных
простых делителях
числа ![]() .
Собрав такую
информацию
для различных
.
Собрав такую
информацию
для различных
![]() ,
в конце концов
удаётся установить,
что
,
в конце концов
удаётся установить,
что ![]() имеет лишь один
простой делитель
и является
простым.
имеет лишь один
простой делитель
и является
простым.
В случае
![]() легко проверить,
что сравнение
из теоремы 3
равносильно
хорошо известному
в элементарной
теории чисел
сравнению
легко проверить,
что сравнение
из теоремы 3
равносильно
хорошо известному
в элементарной
теории чисел
сравнению
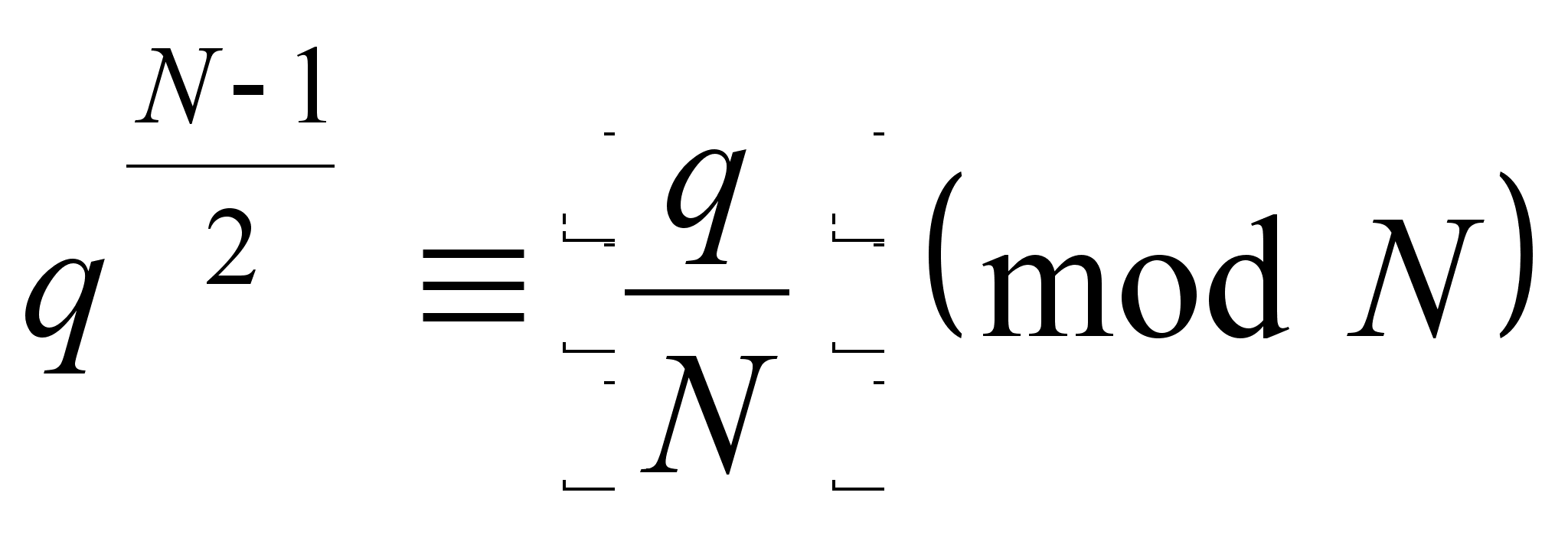 , (13)
, (13)
где ![]() - так называемый
символ Якоби.
Хорошо известно
также, что последнее
сравнение
выполняется
не только для
простых
- так называемый
символ Якоби.
Хорошо известно
также, что последнее
сравнение
выполняется
не только для
простых ![]() ,
но и для любых
целых
,
но и для любых
целых ![]() ,
взаимно простых
с
,
взаимно простых
с ![]() .
Заметим также,
что для вычисления
символа Якоби
существует
быстрый алгоритм,
основанный
на законе взаимности
Гаусса и. в некотором
смысле, подобный
алгоритму
Евклида вычисления
наибольшего
общего делителя.
Следующий
пример показывает.
каким образом
выполнимость
нескольких
сравнений типа
(13) даёт некоторую
информацию
о возможных
простых делителях
числа
.
Заметим также,
что для вычисления
символа Якоби
существует
быстрый алгоритм,
основанный
на законе взаимности
Гаусса и. в некотором
смысле, подобный
алгоритму
Евклида вычисления
наибольшего
общего делителя.
Следующий
пример показывает.
каким образом
выполнимость
нескольких
сравнений типа
(13) даёт некоторую
информацию
о возможных
простых делителях
числа ![]() .
.
Пример
(X.
Ленстра). Пусть
![]() — натуральное
число,
— натуральное
число, ![]() .
для которого
выполнены
сравнения
.
для которого
выполнены
сравнения
 , (14)
, (14)
а кроме
того с некоторым
целым числом
![]() имеем
имеем
![]() . (15)
. (15)
Как уже
указывалось,
при простом
![]() сравнения (14)
выполняются
для любого
сравнения (14)
выполняются
для любого ![]() ,
взаимно простого
с
,
взаимно простого
с ![]() ,
а сравнение
(15) означает, что
,
а сравнение
(15) означает, что
![]() есть первообразный
корень по модулю
есть первообразный
корень по модулю
![]() .
Количество
первообразных
корней равно
.
Количество
первообразных
корней равно
![]() ,
т. е. достаточно
велико. Таким
образом, число
,
т. е. достаточно
велико. Таким
образом, число
![]() с условием
(15) при простом
с условием
(15) при простом
![]() может быть
найдено достаточно
быстро с помощью
случайного
выбора и последующей
проверки (15).
может быть
найдено достаточно
быстро с помощью
случайного
выбора и последующей
проверки (15).
Докажем,
что из выполнимости
(14-15) следует, что
каждый делитель
![]() числа
числа ![]() удовлетворяет
одному из сравнений
удовлетворяет
одному из сравнений
![]() или
или ![]() . (16)
. (16)
Не уменьшая
общности, можно
считать, что
![]() - простое число.
Введем теперь
обозначения
- простое число.
Введем теперь
обозначения
![]() ,
где
,
где ![]() и
и ![]() - нечётные числа.
Из (15) и сравнения
- нечётные числа.
Из (15) и сравнения
![]() следует, что
следует, что
![]() .
Далее, согласно
(14). выполняются
следующие
сравнения
.
Далее, согласно
(14). выполняются
следующие
сравнения
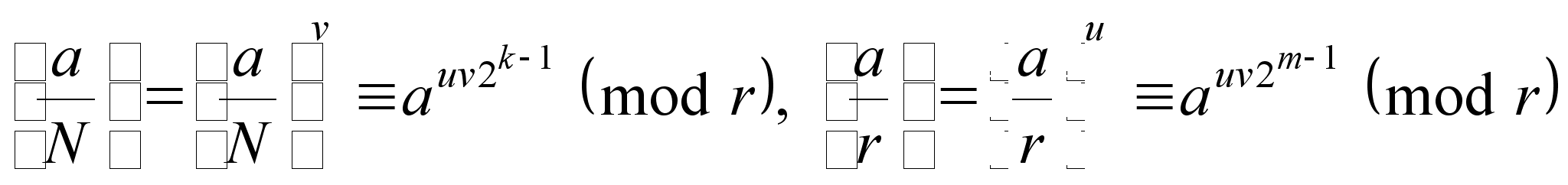 ,
,
означающие (в силу того, что символ Якоби может равняться лишь -1 или +1), что
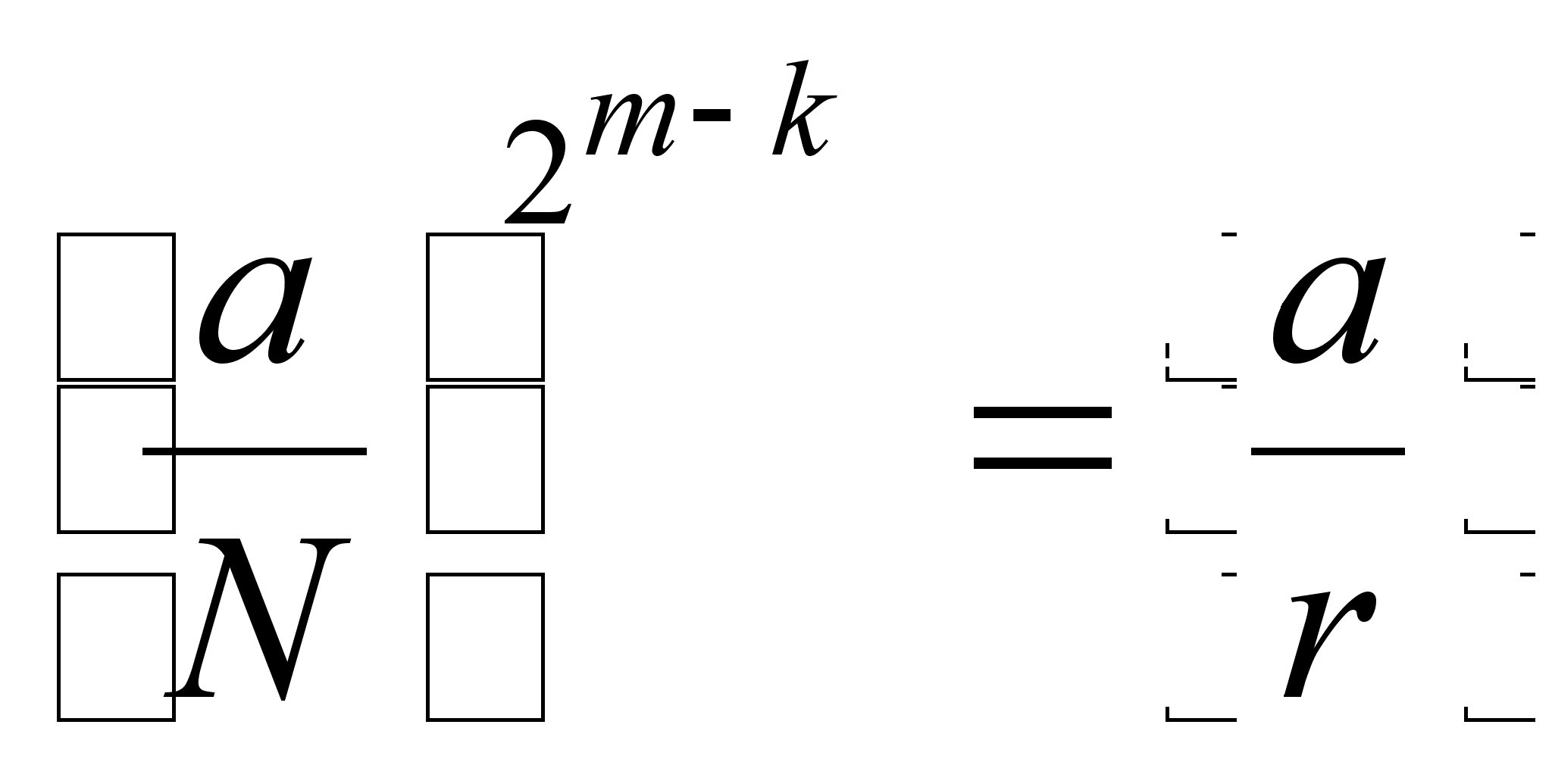 .
.
При ![]() это равенство
означает, что
это равенство
означает, что
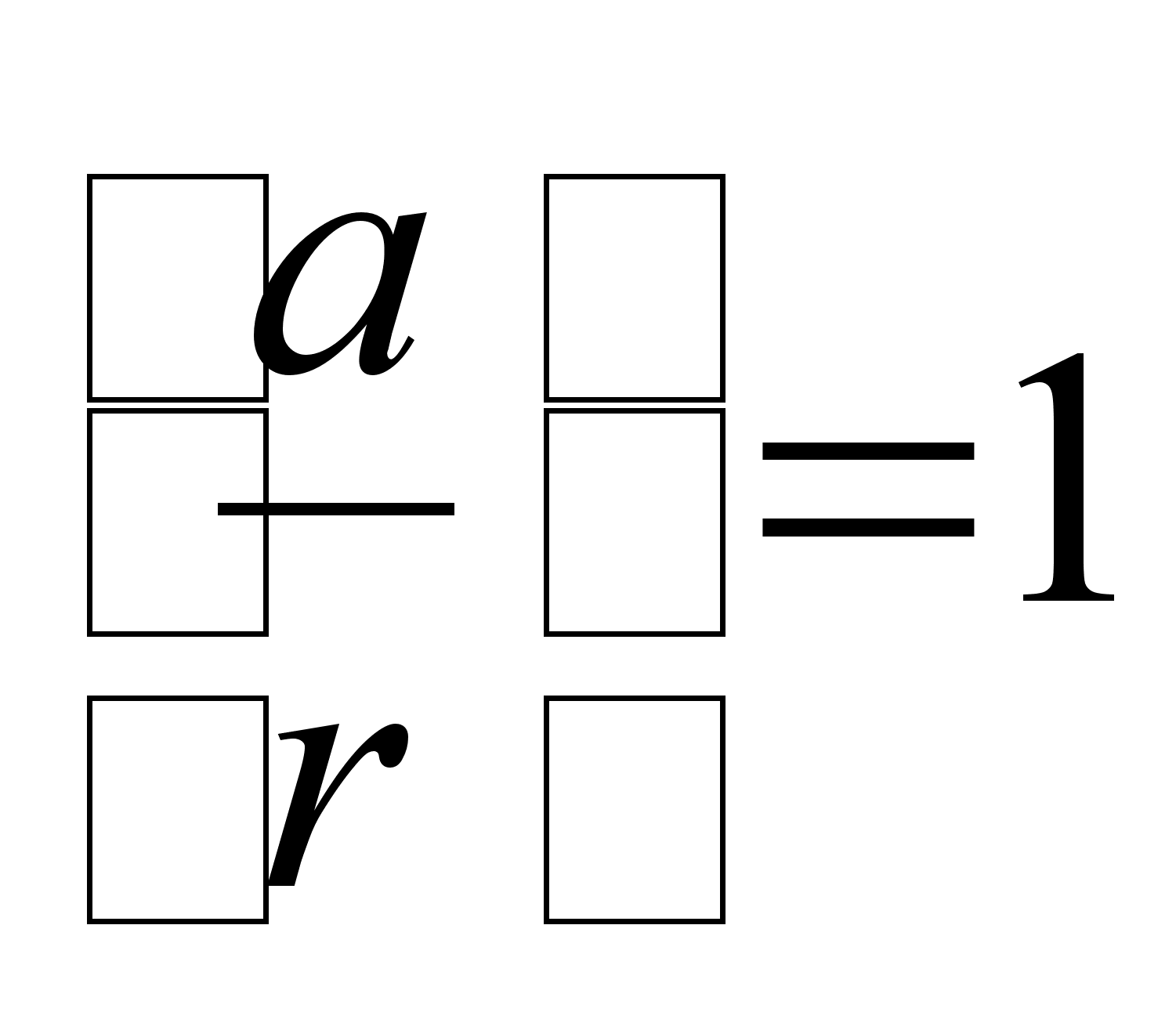 при
при ![]() ,
и, следовательно,
,
и, следовательно,
![]() .
Если же
.
Если же ![]() ,
то имеем
,
то имеем
 и
и ![]() .
Этим (16) доказано.
.
Этим (16) доказано.
Информация
такого рода
получается
и в случае
произвольных
простых чисел
![]() и
и ![]() с указанными
выше свойствами.
с указанными
выше свойствами.
Опишем
схему алгоритма
Адлемана - Ленстры
для проверки
простоты ![]() :
:
1) выбираются
различные
простые числа
![]() и различные
простые нечётные
и различные
простые нечётные
![]() такие, что
такие, что
1) для каждого
![]() все простые
делители числа
все простые
делители числа
![]() содержатся
содержатся
среди
![]() и
и ![]() не делятся на
квадрат простого
числа;
не делятся на
квадрат простого
числа;
1) ![]() .
.
для каждой пары выбранных чисел ![]() ,
, ![]() проводятся тесты, подобные сравнению из теоремы 3. Если
проводятся тесты, подобные сравнению из теоремы 3. Если ![]() не удовлетворяет какому-либо из
не удовлетворяет какому-либо из
этих тестов - оно составное. В противном случае
определяется не очень большое множество чисел, с которыми только и могут быть сравнимы простые делители ![]() . А именно, каждый простой делитель
. А именно, каждый простой делитель ![]() числа
числа ![]() должен удовлетворять сравнению вида
должен удовлетворять сравнению вида
![]() ,
,
![]() .
.
4) проверяется,
содержит ли
найденное
множество
делители ![]() .
Если при этом
делители не
обнаружены,
утверждается,
что
.
Если при этом
делители не
обнаружены,
утверждается,
что ![]() - простое
- простое
число.
Если число
![]() составное, оно
обязательно
имеет простой
делитель
составное, оно
обязательно
имеет простой
делитель ![]() ,
меньший
,
меньший ![]() ,
который сам
содержится
среди возможных
остатков. Именно
на этом свойстве
основано применение
пункта 4) алгоритма.
,
который сам
содержится
среди возможных
остатков. Именно
на этом свойстве
основано применение
пункта 4) алгоритма.
Сумма Якоби

определяется
для двух характеров
![]() модулю
модулю ![]() .
Если характеры
имеют порядок
.
Если характеры
имеют порядок
![]() ,
то соответствующая
сумма Якоби
принадлежит
кольцу
,
то соответствующая
сумма Якоби
принадлежит
кольцу ![]() .
Поскольку числа
.
Поскольку числа
![]() ,
участвующие
в алгоритме,
сравнительно
невелики, то
вычисления
с суммами Якоби
производятся
в полях существенно
меньшей степени,
чем вычисления
с суммами Гаусса.
Это главная
причина, по
которой суммы
Якоби предпочтительнее
для вычислений.
При
,
участвующие
в алгоритме,
сравнительно
невелики, то
вычисления
с суммами Якоби
производятся
в полях существенно
меньшей степени,
чем вычисления
с суммами Гаусса.
Это главная
причина, по
которой суммы
Якоби предпочтительнее
для вычислений.
При ![]() выполняется
классическое
соотношение
выполняется
классическое
соотношение
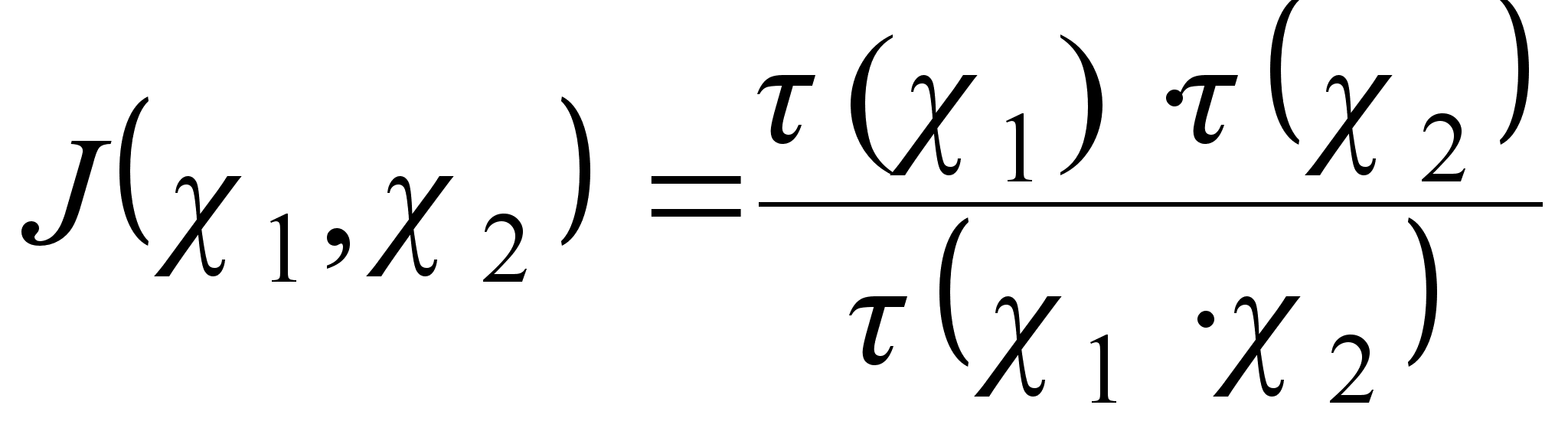
связывающее
суммы Гаусса
с суммами Якоби
и позволяющее
переписать
сравнение
теоремы 3 в терминах
сумм Якоби.
Так. при ![]() и
и ![]() соответствующее
сравнение,
справедливое
для простых
соответствующее
сравнение,
справедливое
для простых
![]() ,
отличных от
2,3,7, принимает
вид
,
отличных от
2,3,7, принимает
вид
![]() ,
,
где ![]() и
и ![]() - некоторый
корень кубический
из 1.
- некоторый
корень кубический
из 1.
В 1984 г. было
внесено существенное
усовершенствование
в алгоритм,
позволившее
освободиться
от требования
неделимости
чисел ![]() на квадраты
простых чисел.
В результате,
например, выбрав
число
на квадраты
простых чисел.
В результате,
например, выбрав
число ![]() и взяв
и взяв ![]() равным произведению
простых чисел
равным произведению
простых чисел
![]() с условием, что
с условием, что
![]() делится на
делится на ![]() ,
получим
,
получим ![]() ,
что позволяет
доказывать
простоту чисел
,
что позволяет
доказывать
простоту чисел
![]() ,
записываемых
сотней десятичных
знаков. При
этом вычисления
будут проводиться
в полях, порождённых
корнями из 1
степеней 16, 9, 5 и
7.
,
записываемых
сотней десятичных
знаков. При
этом вычисления
будут проводиться
в полях, порождённых
корнями из 1
степеней 16, 9, 5 и
7.
Персональный компьютер с процессором Pentium-150. пользуясь реализацией этого алгоритма на языке UBASIC, доказал простоту записываемого 65 десятичными знаками, большего из простых чисел в примере Ривеста, Шамира и Адлемана за 8 секунд. Сравнение этих 8 секунд и 17 лет, потребовавшихся для разложения на множители предложенного в примере числа, конечно, впечатляет.
Отметим,
что опенка
сложности этого
алгоритма
представляет
собой трудную
задачу аналитической
теории чисел.
Как уже указывалось,
количество
операций оценивается
величиной ![]() .
Однако соответствующие
числа
.
Однако соответствующие
числа ![]() и
и ![]() ,
возникающие
в процессе
доказательства,
не могут быть
явно указаны
в зависимости
от
,
возникающие
в процессе
доказательства,
не могут быть
явно указаны
в зависимости
от ![]() .
Доказано лишь
существование
чисел
.
Доказано лишь
существование
чисел ![]() и
и ![]() ,
для которых
достигается
оценка. Впрочем,
есть вероятностный
вариант алгоритма,
доказывающий
простоту простого
числа
,
для которых
достигается
оценка. Впрочем,
есть вероятностный
вариант алгоритма,
доказывающий
простоту простого
числа ![]() с вероятностью
большей
с вероятностью
большей ![]() за
за ![]() арифметических
операций. А в
предположении
расширенной
гипотезы Римана
эта опенка
сложности может
быть получена
при эффективно
указанных
арифметических
операций. А в
предположении
расширенной
гипотезы Римана
эта опенка
сложности может
быть получена
при эффективно
указанных ![]() и
и![]() .
.
Похожие работы
... в тайне. Исходный текст шифруется открытым ключом адресата и передается ему. Зашифрованный текст в принципе не может быть расшифрован тем же открытым ключом. Дешифрование сообщение возможно только с использованием закрытого ключа, который известен только самому адресату. Криптографические системы с открытым ключом используют так называемые необратимые или ...
... . Так как система с открытыми ключами позволяет распределять ключи и в симметричных системах, можно объединить в системе передачи защищенной информации асимметричный и симметричный алгоритмы шифрования. С помощью первого рассылать ключи, вторым же - собственно шифровать передаваемую информацию Обмен информацией можно осуществлять следующим образом: · получатель вычисляет открытый и ...
... схема устройства для аппаратного шифрования информации, которая соответствует приведенным выше требованиям, изображена на рисунке 1.9. Рис. 1.9 – Структурная схема устройства аппаратного шифрования 2. РАЗРАБОТКА СХЕМОТЕХНИЧЕСКОЙ РЕАЛИЗАЦИИ АППАРАТНОГО ШИФРАТОРА 2.1 Выбор элементной базы для шифратора Согласно техническому заданию, элементная база для аппаратного шифратора должна ...
... не к ключам!) и поэтому может зашифровывать и дешифровывать любую информацию; 2.7 Выводы по разделу 2. Подводя итоги вышесказанного, можно уверенно заявить, что криптографическими системами защиты называються совокупность различных методов и средств, благодаря которым исходная информация кодируеться, передаеться и расшифровываеться. Существуют различные криптографические системы защиты, ...





0 комментариев