Навигация
Дослідження функції та побудова графіка
2.2. Дослідження функції та побудова графіка
Загально відомою є схема дослідження функції для побудови графіка:
1) знайти область визначення функції та множину її значень;
2) дослідити функцію на парність та непарність, періодичність;
3) знайти точки перетину графіка функції з осями системи координат, точки розриву, проміжки знакосталості функції;
4) дослідити поводження функції біля точок розриву та на нескінченності, знайти якщо вони є, асимптоти графіка;
5) знайти нулі та точки розриву похідної, інтервали монотонності функції, точки екстремуму та екстремальні значення функції;
6) знайти нулі та точки розриву другої похідної, інтервали опуклості графіка функції, точки перегину та значення функції в цих точках;
7) для побудови графіка необхідно знайти достатню кількість контрольних точок, через які він проходить.
Зауважу, що на практиці не завжди є потреба досліджувати функцію за наведеною схемою і в такій саме послідовності.
Так, наприклад, множину значень деяких функцій можна встановити лише після знаходження екстремальних значень функції та її поводження біля точок розриву і на нескінченності.
Можна спочатку знайти нулі функції. Якщо вони розташовані не симетрично відносно нуля, то функція не може бути ні непарною, ні парною, ні періодичною. Такий же висновок можна зробити у випадку, коли функція має область визначення не симетричну відносно нуля, то, зрозуміло, що з такого факту ми не можемо робити висновок про парність або непарність. Проте, якщо нулі функції симетричні відносно нуля, але їх число скінчене, то вона не є періодичною.
Не може бути функція ні парною, ні непарною, ні періодичною, якщо нулі першої або другої похідних розміщені несиметрично відносно нуля.
Аналогічно можна зробити висновок і з несиметричного розміщення точок розриву.
Для складних функцій ![]() можна керуватися такими простими твердженнями:
можна керуватися такими простими твердженнями:
1. якщо функція ![]() парна, то складна функція також парна;
парна, то складна функція також парна;
2. якщо функція ![]() і
і ![]() непарні, то складна функція непарна;
непарні, то складна функція непарна;
3. якщо ![]() непарна, а функція
непарна, а функція![]() парна, то складна функція парна;
парна, то складна функція парна;
4. якщо функція ![]() періодична, то і складна функція
періодична, то і складна функція ![]() періодична, причому її період може бути меншим за період функції
періодична, причому її період може бути меншим за період функції ![]() , але не більшим; їх періоди збігаються, якщо функція f строго монотонна.
, але не більшим; їх періоди збігаються, якщо функція f строго монотонна.
Зручно користуватися такими твердженнями:
1. сума скінченого числа парних (непарних) функцій є парною (непарною) функцією;
2. добуток парних функцій є парною функцією;
3. добуток непарних функцій є парною функцією, якщо число функцій-множників – парне число, і непарною, якщо число функцій-множників непарне;
4. добуток(частка) парної і непарної функції є функцією непарною.
Дослідимо функції та побудуємо їх графіки.
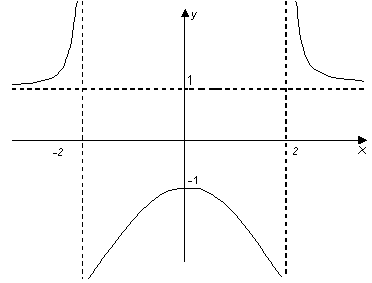
Приклад 1. Побудувати графік функції
![]()
Розв’язання.
1) Область визначення функції f :
Х=![]()
![]()
![]()
![]()
![]() .
.
2) Функція парна. Тому її графік симетричний відносно осі ординат.
3) Функція не є періодичною. Це випливає навіть з того, що вона невизначена лише у двох точках.
4) Графік функції перетинає вісь ординат у точці (0;1). Нулі функції відсутні. Отже, графік функції не перетинає вісь абсцис.
5) Дослідимо функцію на монотонність та критичні точки. Для цього знайдемо похідну
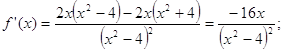
![]() ;
;
х=0–критична точка.
Для ![]()
![]()
![]()
![]()
![]() . Отже, на цих проміжках функція зростає. Оскільки функція парна, то на проміжках
. Отже, на цих проміжках функція зростає. Оскільки функція парна, то на проміжках ![]()
![]()
![]() вона спадає. Тоді точка х=0 є точкою локального максимуму. Знайдемо його значення
вона спадає. Тоді точка х=0 є точкою локального максимуму. Знайдемо його значення
![]() .
.
6) Дослідимо функцію на опуклість та точки перегину:

 .
.
На проміжках ![]()
![]()
![]()
![]() . Отже, графік функції опуклий вниз. На проміжку
. Отже, графік функції опуклий вниз. На проміжку ![]()
![]() , а тому графік функції опуклий вгору.
, а тому графік функції опуклий вгору.
Точки перегину відсутні.
7) Оскільки ![]() , то пряма у=1 є горизонтальною асимптотою для графіка функції.
, то пряма у=1 є горизонтальною асимптотою для графіка функції.
Дослідимо поведінку функції біля точок х=2, х=-2:
![]() ,
, ![]() .
.
Отже, в точці х=2 функція має розрив другого роду, а пряма х=2 є вертикальною асимптотою. Враховуючи парність функції, робимо висновки, що пряма х=-2 також є вертикальною асимптотою.
 .
.
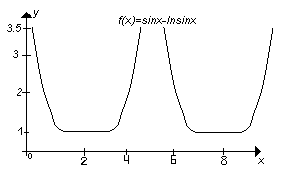
Приклад 2. Побудувати графік функції:
![]()
Розв’язання.
1. Область визначення функції f :
![]() .
.
2. Функція не належить ні до парних, ні до непарних. Це безпосередньо випливає з того, що область її визначення несиметрична відносно нуля.
3. Період функції ![]() . Тому дослідження функції достатньо спочатку провести на проміжку
. Тому дослідження функції достатньо спочатку провести на проміжку ![]() . Крім того, враховуючи, що
. Крім того, враховуючи, що ![]() , робимо висновок про симетричність графіка відносно прямої
, робимо висновок про симетричність графіка відносно прямої ![]() на проміжку
на проміжку ![]() . Тому можна обмежитися дослідженням функції на проміжку
. Тому можна обмежитися дослідженням функції на проміжку ![]() .
.
4. Дослідимо функцію на монотонність та критичні точки на проміжку ![]() . Для цього знайдемо її похідну
. Для цього знайдемо її похідну
![]() .
.
Для ![]()
![]()
![]() . Тому функція на цьому проміжку спадає. Тоді на проміжку
. Тому функція на цьому проміжку спадає. Тоді на проміжку ![]() вона зростає, а в точці
вона зростає, а в точці ![]() має мінімум, який дорівнює 1.
має мінімум, який дорівнює 1.
Враховуючи періодичність функції, робимо висновок, що вона на проміжках![]() і зростає на проміжках
і зростає на проміжках ![]() ,
, ![]() . В точках
. В точках ![]() набуває мінімального значення, яке дорівнює 1.
набуває мінімального значення, яке дорівнює 1.
5. Дослідимо функцію на опуклість на проміжку ![]() :
:
![]() .
.
Звідси безпосередньо випливає, що для ![]()
![]() . Отже, графік функції опуклий вниз. Тоді і на проміжку
. Отже, графік функції опуклий вниз. Тоді і на проміжку ![]() він опуклий вниз. Таким чином, на проміжках
він опуклий вниз. Таким чином, на проміжках ![]() графік функції опуклий вниз.
графік функції опуклий вниз.
6. Визначимо поведінку функції біля нуля справа і біля ![]() зліва:
зліва:
![]()
![]() .
.
Отже, прямі х=0, х=![]() – вертикальні асимптоти. Тоді і прямі х=
– вертикальні асимптоти. Тоді і прямі х=![]() ,
,![]() – вертикальні асимптоти.
– вертикальні асимптоти.
Похожие работы
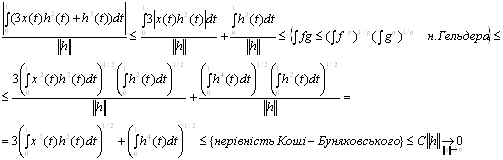
... говорять про похідну за напрямком , розуміючи під цим границю відношення при умові, що вона існує; цю границю позначають . Ясно, що , де – одиничний вектор напрямку , тобто . Зауваження. Похідна Фреше і похідна за напрямком є елементами різної природи: є лінійний оператор з X в Y, в той час як є елементом простору Y. Якщо відображення диференційовне в точці за Фреше, то воно диференційовне ...
... запам’ятовуванню за рахунок активізації декількох аналізаторів: слуху, зору та підтримання постійного контакту з учнями під час уроку. ЛІТЕРАТУРА Махмутов М. Й. Проблемноє обучение. -М.: Педагогика, 1975. – 240 с. Методи обучения математике / Под ред. А. А. Столяра. –Минск.: Висш. шк.,1981. – 398 с. Г.П.Бевз. Методика викладання математики. 3-видання. -К.: Вища школа, 1989. – 352 с. Н.В. ...
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... може бути компетентною або некомпетентною в певних питаннях, тобто мати компетентність (компетентності) у певній галузі діяльності. Саме тому, одним із результатів навчання курсу «Застосування ІКТ у навчальному процесі з математики» вбачається формування в майбутніх вчителів відповідних ключових фахових компетентностей. Зазначене вище наштовхнуло на дослідження компетентностей: внаслідок чого ...
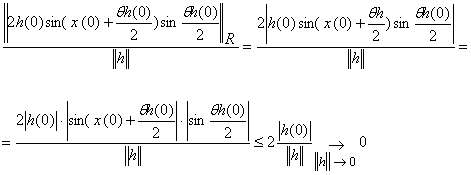
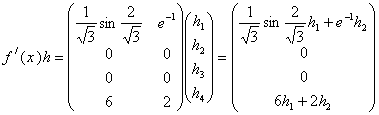






0 комментариев