Навигация
Похідна Фреше та похідна Гато
Дніпропетровський національний університет
Факультет механіко-математичний
Кафедра математичного аналізу
БАКАЛАВРСЬКА ДИПЛОМНА РОБОТА“Похідна Фреше та похідна Гато”
Виконавець:Керівник роботи:
студентка 4 курсу доцент
Дніпропетровськ
200_
РЕФЕРАТ
Випускна робота: 40 с., 4 джерела
Об’єктом дослідження є похідні Фреше та Гато.
Мета роботи – дослідити похідні Фреше та Гато у різних просторах.
Методи дослідження – методи функціонального аналізу.
Результати досліджень можуть бути застосовані при вивченні спеціальних курсів.
Ключові слова: ДИФЕРЕНЦІЙОВНІСТЬ, ПОХІДНІ ФРЕШЕ ТА ГАТО, ЛІНІЙНИЙ НОРМОВАНИЙ ПРОСТІР.
RESUME
The graduation research of the fourth year student Lisnyak Ludmila (DNU, Faculty of Mechanics and Mathematics, Department of Mathematical Analysis) deals with Freshe’s and Gato’s derivatives. The work is interesting for student and post- graduate student.
Bibliog. 4
ЗМІСТ
ВСТУП
РОЗДІЛ 1. ЕЛЕМЕНТИ ДИФЕРЕНЦІАЛЬНОГО ТА ІНТЕГРАЛЬНОГО ЧИСЛЕННЯ В ЛІНІЙНИХ НОРМОВАНИХ ПРОСТОРАХ1.1 Диференціал та похідна Фреше
1.2 Основні теореми
1.3 Похідна Гато
1.3.1 Основні теореми
1.3.2 Похідні по підпростору РОЗДІЛ 2. ПОХІДНІ ФРЕШЕ ТА ГАТО В ПРИКЛАДАХ І ЗАДАЧАХ Список використаних джерелВСТУП
Деякі задачі, які виникають в функціональному аналізі, носять суттєво нелінійний характер, вони приводять до необхідності розвивати поряд з “лінійним” і “нелінійний” функціональний аналіз, а саме вивчати нелінійні функціонали й нелінійні оператори в нескінченновимірних просторах. До нелінійного функціонального аналізу відноситься така класична область математики як варіаційне числення, підвалини якого буди закладені ще в XVII-XVIII століттях в роботах Я. Бернуллі, Л. Ейлера, Ж. Лагранжа. Але в цілому нелінійний функціональний аналіз являє собою нову область математики, поки ще далеку від свого завершення. В роботі викладено деякі початкові поняття, які відносяться до нелінійного функціонального аналізу, а саме до теорії диференціювання, і деякі застосування цих понять.
Визначення похідної Фреше, яке нині загальноприйняте, вперше з’явилось в лекціях К. Вейерштраса (1861). В кінці 19 століття це визначення почало входити до підручників. Але до моменту, коли М. Фреше почав розробку нескінченновимірного аналізу, класичне нині визначення диференціала було настільки не загальноприйнятим, що й сам Фреше вважав, що визначений ним диференціал на нескінченновимірному просторі є новим поняттям і в скінчено вимірному випадку. Тепер термін вживається тільки при розгляді нескінченновимірних відображень.
Визначення варіації Гато було введено в 1913-14 роках Р. Гато (R.Gateaux). Для функціоналів класичного варіаційного числення це визначення було дано Ж. Лагранжем.
Нехай ![]() – сукупність усіх відображень з
– сукупність усіх відображень з ![]() в
в ![]() (
(![]() – лінійні топологічні простори), і
– лінійні топологічні простори), і ![]() – деяка топологія в
– деяка топологія в ![]() . В залежності від вибору
. В залежності від вибору ![]() в
в ![]() можна отримати різні визначення похідних. Якщо обираємо
можна отримати різні визначення похідних. Якщо обираємо ![]() – топологію поточкової збіжності, то отримаємо диференційовність по Гато. Якщо
– топологію поточкової збіжності, то отримаємо диференційовність по Гато. Якщо ![]() банахові простори, а топологія
банахові простори, а топологія ![]() в
в ![]() є топологією рівномірної збіжності на обмежених множинах в
є топологією рівномірної збіжності на обмежених множинах в ![]() , то приходимо до диференційовності по Фреше.
, то приходимо до диференційовності по Фреше.
РОЗДІЛ 1
ЕЛЕМЕНТИ ДИФЕРЕНЦІАЛЬНОГО ТА ІНТЕГРАЛЬНОГО ЧИСЛЕННЯ В ЛІНІЙНИХ НОРМОВАНИХ ПРОСТОРАХВ розділі 1 ми розглянемо різні означення похідної відображення лінійних нормованих просторів та деякі їх застосування.
1.1 Диференціал та похідна Фреше
Нехай X та Y – лінійні нормовані простори, G – відкрита множина простору X. Відображення (функція, оператор) ![]() називається диференційовним за Фреше в точці
називається диференційовним за Фреше в точці ![]() , якщо існує неперервний лінійний оператор
, якщо існує неперервний лінійний оператор ![]() , такий, що для будь-якого
, такий, що для будь-якого ![]() , яке задовольняє умові
, яке задовольняє умові ![]() ,
,
![]() ,
,
де ![]() , якщо
, якщо ![]() в смислі збіжності за нормою в просторі Y.
в смислі збіжності за нормою в просторі Y.
Головна частина ![]() , яка лінійно залежить від
, яка лінійно залежить від ![]() , приріст
, приріст ![]() називається диференціалом Фреше відображення f в точці x та позначається
називається диференціалом Фреше відображення f в точці x та позначається ![]() , а вираз
, а вираз ![]() називається остачею приросту.
називається остачею приросту.
Таким чином, ![]() та приріст
та приріст ![]() оператора записується у вигляді
оператора записується у вигляді
![]() ,
,
де
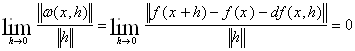
Лінійний оператор ![]() називається похідною Фреше відображення
називається похідною Фреше відображення ![]() в точці
в точці ![]() та позначається
та позначається ![]() . Тобто,
. Тобто, ![]() .
.
Відображення, диференційовне в кожній точці множини G називається диференційовним на G.
Доведемо, що похідна диференційованого відображення визначається однозначно. Нехай ![]() – інший неперервний лінійний оператор такий, що
– інший неперервний лінійний оператор такий, що
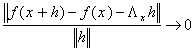 ,
,
якщо ![]() . Тоді
. Тоді
 ,
,
якщо ![]() . Покладемо
. Покладемо ![]() , де
, де ![]() – довільний ненульовий елемент простору X. Якщо
– довільний ненульовий елемент простору X. Якщо ![]() , то
, то ![]() і ми знаходимо
і ми знаходимо
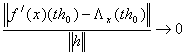 .
.
В силу лінійності ![]() та
та ![]() це означає, що
це означає, що
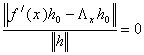 ,
,
тобто ![]() . Оскільки оператори
. Оскільки оператори ![]() та
та ![]() в нулі дорівнюють нулю, то
в нулі дорівнюють нулю, то ![]() при будь-яких
при будь-яких ![]() . Однозначність визначення похідної доведено.
. Однозначність визначення похідної доведено.
Приклад 1. Нехай відображення ![]() , де
, де ![]() і
і ![]() відкрито.
відкрито.
Тоді наведені вище означення диференційовності відображення і похідної співпадають з означеннями диференційовності та похідної векторної функції векторного аргументу. В цьому випадку ![]() є лінійним оператором, який визначається матрицею
є лінійним оператором, який визначається матрицею 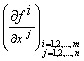 , де
, де ![]() – координатні функції відображення
– координатні функції відображення ![]() .
.
Приклад 2. Нехай ![]() – гільбертов простір,
– гільбертов простір, ![]() і
і ![]() . Нехай спочатку
. Нехай спочатку ![]() . Тоді
. Тоді
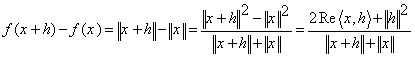 (1)
(1)
Оскільки ![]() , то
, то
![]() , (2)
, (2)
де ![]() при
при ![]() . Із рівностей (1) та (2) випливає, що
. Із рівностей (1) та (2) випливає, що
![]() ,
,
де ![]() – лінійний по
– лінійний по ![]() функціонал і
функціонал і
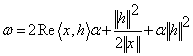 .
.
Оскільки ![]() , то
, то ![]() при
при ![]() . Таким чином,
. Таким чином, ![]() диференційовна в будь-якій ненульовій точці
диференційовна в будь-якій ненульовій точці ![]() простору
простору ![]() і
і
![]() .
.
Нехай тепер ![]() . Тоді
. Тоді ![]() . Покажемо, що не існує елемента
. Покажемо, що не існує елемента ![]() такого, що при всіх достатньо малих
такого, що при всіх достатньо малих ![]()
![]() , (3)
, (3)
де ![]() при
при ![]() . Якщо б це було так, то також
. Якщо б це було так, то також
![]() , або
, або ![]() , (4)
, (4)
де ![]() при
при ![]() . Але тоді з рівностей (3) та (4) випливає
. Але тоді з рівностей (3) та (4) випливає ![]() при
при ![]() , що неможливо.
, що неможливо.
Таким чином, відображення ![]() не диференційовне за Фреше в точці
не диференційовне за Фреше в точці ![]() .
.
Приклад 3. Нехай ![]() і
і 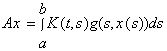 , де ядро
, де ядро ![]() неперервне в квадраті
неперервне в квадраті ![]() ,
, ![]() – функція двох змінних, визначена в полосі
– функція двох змінних, визначена в полосі ![]() і неперервна в цій області. Тоді
і неперервна в цій області. Тоді ![]() – функція, визначена на
– функція, визначена на ![]() і яка приймає значення в цьому ж просторі.
і яка приймає значення в цьому ж просторі.
Припустимо, що функція ![]() не тільки неперервна, але й має частинну похідну
не тільки неперервна, але й має частинну похідну![]() , рівномірно неперервну в полосі
, рівномірно неперервну в полосі ![]() .
.
Тоді ![]() – диференційовна функція. А саме, для довільної функції
– диференційовна функція. А саме, для довільної функції ![]() маємо
маємо
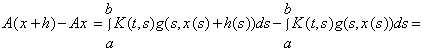
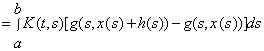
За теоремою Лагранжа,
![]() ,
,
де
![]() . Далі, маємо
. Далі, маємо
![]() .
.
При ![]() , тобто при
, тобто при ![]() рівномірно на
рівномірно на ![]() , також
, також ![]() рівномірно на
рівномірно на ![]() , оскільки функція, неперервна в замкненій обмеженій області
, оскільки функція, неперервна в замкненій обмеженій області ![]() , рівномірно неперервна в цій області. Тому
, рівномірно неперервна в цій області. Тому
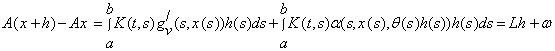 ,
,
де
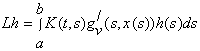 і
і 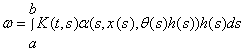 .
.
При цьому
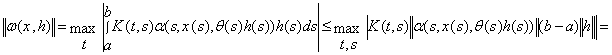
![]() і тому
і тому ![]() при
при ![]() .
.
Таким чином, ![]() диференційовна за Фреше і
диференційовна за Фреше і
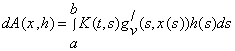 .
.
Приклад 4. Якщо ![]() і границя
і границя ![]() існує, то
існує, то ![]() диференційовне в точці
диференційовне в точці ![]() і
і ![]() . Дійсно, в цьому випадку
. Дійсно, в цьому випадку ![]() , де
, де ![]() при
при ![]() , і диференційованість
, і диференційованість ![]() очевидна.
очевидна.
Множина відображень, визначених в околі точки ![]() , які приймають значення в просторі Y та диференційовних в точці
, які приймають значення в просторі Y та диференційовних в точці ![]() , є лінійною системою , а також оператор диференціювання є лінійним, тобто
, є лінійною системою , а також оператор диференціювання є лінійним, тобто
![]() ,
,
або, інакше,
![]() .
.
Далі, з рівності
![]()
випливає, що функція ![]() , диференційовна в точці
, диференційовна в точці ![]() , неперервна в цій точці.
, неперервна в цій точці.
Обернене твердження не вірне (приклад 2).
Якщо ![]() – лінійний неперервний оператор, що діє з X в Y, то для будь-якого
– лінійний неперервний оператор, що діє з X в Y, то для будь-якого ![]() маємо
маємо ![]() . Дійсно, тоді при всіх
. Дійсно, тоді при всіх ![]()
![]() ,
,
звідки й випливає наведене твердження.
Слід зазначити, що відображення ![]() та
та ![]() , які мають область визначення в одному і тому просторі, діють в різні простори, а саме
, які мають область визначення в одному і тому просторі, діють в різні простори, а саме ![]() , а
, а ![]() . Якщо
. Якщо ![]() диференційовне всюди на G, то
диференційовне всюди на G, то ![]() ,
, ![]() .
.
Похожие работы
... Чарка, стакан 4 320 2 80 400 Столові прибори (комплект) 4 320 2 80 400 Далі наведемо характеристику посуду, який будуть використовувати в комплексному закладі ресторанного господарства (табл. 2.8–2.11). Таблиця 2.8. Характеристика та призначення класичного вітчизняного порцелянового та фаянсового посуду Найменування Розміри, мм Місткість, см3, порцій Призначення ...
... ється, окремими технологічними операціями, специфічними виглядом і смаком, енергетичною цінністю та іншими ознаками. Варені ковбаси займають 53-60% в загальному виробництві ковбасних виробів. 3.1 Характеристика підприємства Ковбасний цех спільного підприємства Сумський виробничий комбінат розміщєно напівнічному-сході м. Суми, на відстані 1000 м від житлових кварталів. Окрім ковбасного цуху ...
0 комментариев