Навигация
Исследование стационарного режима в сети с динамическим протоколом случайного множественного доступа для конечного числа станций
4. Исследование стационарного режима в сети с динамическим протоколом случайного множественного доступа для конечного числа станций
Рассматривается сеть связи, состоящая из конечного числа малых абонентских станций, центральной станции и спутника ретранслятора. Спутник, приняв сообщение от периферийной станции передает его на центральную. Так как спутниковый канал связи совместно используют все станции, то возможно совпадение времени ретрансляции сообщений, при этом сообщения искажаются (попадают в конфликт) и требуют повторной передачи. Архитектура подобных сетей связи позволяет реализовать протоколы случайного множественного доступа с оповещением о конфликте, в которых для избежания искажения других сообщений, центральной станцией рассылается сигнал оповещения о конфликте. Сообщения, попавшие в конфликт, должны будут переданы абонентскими станциями повторно после случайной задержки для избежания повторных конфликтов.
Математической моделью рассматриваемой сети связи может служить однолинейная система массового обслуживания, на вход которой поступает примитивный поток неповторных требований с параметром ![]() , где N – число периферийных абонентских станций сети, i – число тех АС, которые либо передают свои сообщения, либо осуществляют их случайную задержку для повторной передачи,
, где N – число периферийных абонентских станций сети, i – число тех АС, которые либо передают свои сообщения, либо осуществляют их случайную задержку для повторной передачи, ![]() , если обслуживающий канал (спутник) свободен,
, если обслуживающий канал (спутник) свободен, ![]() , если обслуживающий канал осуществляет успешную передачу.
, если обслуживающий канал осуществляет успешную передачу.
Каждое требование в момент поступления в систему встает на прибор и начинает обслуживаться. Отправив заявку на обслуживание, АС не генерирует других заявок до тех пор, пока отправленная заявка не обслужится успешно. Обслуживание экспоненциальное с параметром m. Если за время обслуживания какого-либо требования другие заявки не поступали в систему, то исходное требование считается успешно обслуженным и покидает систему. В противном случае, т.е. когда одновременно обслуживались два или более требований, происходит конфликт. Продолжительность этапа оповещения о конфликте распределена по экспоненциальному закону с параметром ![]() . Заявки, попавшие в конфликт, переходят в ИПВ, откуда пытаются встать на обслуживание вновь через экспоненциально (с параметром
. Заявки, попавшие в конфликт, переходят в ИПВ, откуда пытаются встать на обслуживание вновь через экспоненциально (с параметром ![]() ) распределенную задержку. Структура такой СМО имеет вид рис. 4.1.
) распределенную задержку. Структура такой СМО имеет вид рис. 4.1.
 | |||||||
 | |||||||
| |||||||
![]()
| ||||||||||||||||
 | ||||||||||||||||
| ||||||||||||||||
 | ||||||||||||||||
Рис. 4.1 – Модель системы массового обслуживания
Состояние исследуемой сети связи можно описать двумерной случайной величиной ![]() , изменение во времени которой образует двумерный процесс
, изменение во времени которой образует двумерный процесс ![]() .
.
Случайная величина ![]() описывает состояние обслуживающего канала в момент времени t и принимает три значения:
описывает состояние обслуживающего канала в момент времени t и принимает три значения:
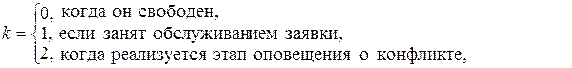
величина ![]() показывает число заявок в ИПВ в момент времени t .
показывает число заявок в ИПВ в момент времени t .
Рассмотрим вероятности переходов из состояния системы ![]() в произвольный момент времени t в состояние
в произвольный момент времени t в состояние ![]() за бесконечно малый интервал времени
за бесконечно малый интервал времени ![]() .
.
1. Пусть система находится в состоянии ![]() , то есть в ИПВ находится i заявок и прибор свободен, за интервал времени
, то есть в ИПВ находится i заявок и прибор свободен, за интервал времени ![]() состояние системы может измениться таким образом:
состояние системы может измениться таким образом:
а) с вероятностью ![]() из входящего потока требований поступит новая заявка, которая немедленно займет прибор и начнет обслуживание, тогда система в момент времени
из входящего потока требований поступит новая заявка, которая немедленно займет прибор и начнет обслуживание, тогда система в момент времени ![]() будет находиться в состоянии
будет находиться в состоянии ![]() ;
;
б) с вероятностью ![]() к прибору обратится одна из i заявок, находящихся в ИПВ и система перейдет в состояние
к прибору обратится одна из i заявок, находящихся в ИПВ и система перейдет в состояние ![]() ;
;
в) с вероятностью 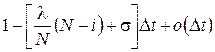 состояние системы не изменится.
состояние системы не изменится.
2. Пусть система в момент времени t находится в состоянии ![]() , то есть прибор занят обслуживанием заявки и в ИПВ находится i требований, за интервал времени
, то есть прибор занят обслуживанием заявки и в ИПВ находится i требований, за интервал времени ![]() возможны следующие переходы:
возможны следующие переходы:
а) с вероятностью ![]() прибор успешно завершит обслуживание, и в момент времени
прибор успешно завершит обслуживание, и в момент времени ![]() система будет находиться в состоянии
система будет находиться в состоянии ![]() ;
;
б) с вероятностью ![]() в систему поступит новое требование из входящего потока, произойдет конфликт. Как вновь поступившая, так и заявка с прибора перейдут в ИПВ, и начнется интервал оповещения о конфликте, следовательно, система перейдет в состояние
в систему поступит новое требование из входящего потока, произойдет конфликт. Как вновь поступившая, так и заявка с прибора перейдут в ИПВ, и начнется интервал оповещения о конфликте, следовательно, система перейдет в состояние ![]() ;
;
в) с вероятностью ![]() к прибору обратится одна из заявок с ИПВ, произойдет конфликт, и обе заявки переместятся в ИПВ, следовательно,
к прибору обратится одна из заявок с ИПВ, произойдет конфликт, и обе заявки переместятся в ИПВ, следовательно,
система в момент времени ![]() будет находиться в состоянии
будет находиться в состоянии ![]() ;
;
г) с вероятностью  состояние системы не изменится.
состояние системы не изменится.
3. Пусть система в момент времени t находится в состоянии ![]() . Посмотрим, что произойдет через интервал времени длины
. Посмотрим, что произойдет через интервал времени длины ![]() :
:
а) с вероятностью ![]() к прибору обратится заявка из входящего потока, которая автоматически попадет в ИПВ. В момент времени
к прибору обратится заявка из входящего потока, которая автоматически попадет в ИПВ. В момент времени ![]() система будет в состоянии
система будет в состоянии ![]() ;
;
б) с вероятностью ![]() интервал оповещения о конфликте завершится, и система перейдет в состояние
интервал оповещения о конфликте завершится, и система перейдет в состояние ![]() ;
;
в) с вероятностью  состояние системы не изменится.
состояние системы не изменится.
Все остальные вероятности переходов не превышают порядка малости ![]() .
.
Процесс ![]() является марковским, распределение которого
является марковским, распределение которого
![]()
в стационарном режиме удовлетворяет системе уравнений
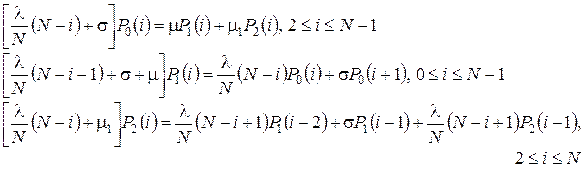 (4.1)
(4.1)
4.1. Асимптотический анализ распределения вероятностей состояний сети
Систему уравнений (4.1) будем решать асимптотическим методом марковизируемых систем [7] при ![]() .
.
Первое приближение
В системе уравнений (4.1) сделаем следующие замены переменных: ![]() . В результате такой замены производится переход от дискретной переменной
. В результате такой замены производится переход от дискретной переменной ![]() к непрерывной переменной
к непрерывной переменной ![]() . В новых обозначениях система (4.1) примет вид
. В новых обозначениях система (4.1) примет вид
 (4.2)
(4.2)
Получим вид решения системы (4.2), которую будем решать в два этапа.
1 этап. Устремим ![]() к нулю и обозначим
к нулю и обозначим ![]() . Тогда система (4.2) перейдет в систему
. Тогда система (4.2) перейдет в систему
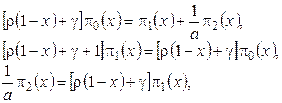 (4.3)
(4.3)
решение которой имеет вид
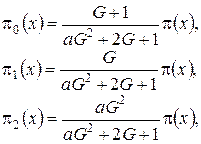 (4.4)
(4.4)
где ![]()
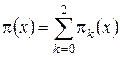 – асимптотическая плотность распределения вероятностей нормированного числа заявок в ИПВ.
– асимптотическая плотность распределения вероятностей нормированного числа заявок в ИПВ.
Осталось найти вид функции ![]() , для этого перейдем ко второму этапу.
, для этого перейдем ко второму этапу.
2 этап. В системе (4.2) все функции с аргументом ![]() разложим в ряд по приращению аргумента
разложим в ряд по приращению аргумента ![]() , ограничиваясь слагаемыми порядка
, ограничиваясь слагаемыми порядка ![]() , получим
, получим
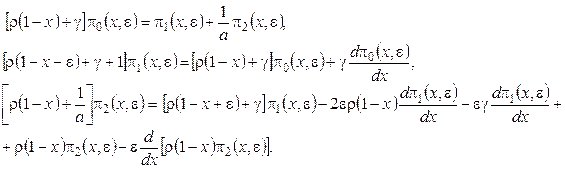 (4.5)
(4.5)
Сложив все уравнения системы, будем иметь
![]() (4.6)
(4.6)
В полученном равенстве поделим левую и правую части на ![]() и
и ![]() , прейдем к такому равенству
, прейдем к такому равенству
![]() (4.7)
(4.7)
Подставим в (4.7) функции ![]() в форме (4.4) и получим
в форме (4.4) и получим
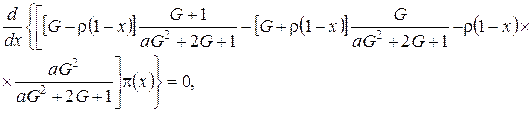 (4.8)
(4.8)
следовательно
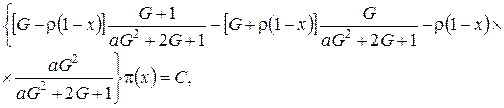 (4.9)
(4.9)
где С – некоторая постоянная.
Необходимо найти константу C. Нетрудно заметить, что при х=0 выражение в фигурных скобках не положительно, следовательно ![]() , а при х=1
, а при х=1 ![]() . Итак,
. Итак, ![]() . Таким образом, произведение двух функций равно нулю, следовательно,
. Таким образом, произведение двух функций равно нулю, следовательно, ![]() может принимать какое-либо ненулевое значение лишь в тех точках, в которых выражение в скобках равно нулю.
может принимать какое-либо ненулевое значение лишь в тех точках, в которых выражение в скобках равно нулю.
Получим функцию ![]() , везде равную нулю, за исключением точек, являющихся корнями уравнения
, везде равную нулю, за исключением точек, являющихся корнями уравнения
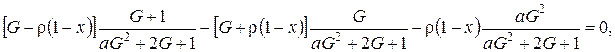
после преобразований это выражение принимает вид
![]() (4.10)
(4.10)
Так как ![]() – плотность распределения вероятностей, то должно выполняться условие нормировки
– плотность распределения вероятностей, то должно выполняться условие нормировки 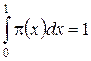 . Этим условиям удовлетворяет лишь функция вида
. Этим условиям удовлетворяет лишь функция вида
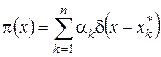 ,
,
где ![]() – корни уравнения (4.10), n – число корней,
– корни уравнения (4.10), n – число корней, 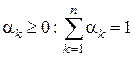 .
.
Если уравнение (4.10) имеет единственный корень ![]() , то эту точку назовем точкой стабилизации, потому что она является модой распределения вероятностей нормированного процесса заявок в ИПВ
, то эту точку назовем точкой стабилизации, потому что она является модой распределения вероятностей нормированного процесса заявок в ИПВ ![]() , и в ее окрестности достаточно долго флуктуируют значения этого процесса. В этом случае назовем сеть моностабильной.
, и в ее окрестности достаточно долго флуктуируют значения этого процесса. В этом случае назовем сеть моностабильной.
Второе приближение
Пусть уравнение (4.10) имеет единственный корень ![]() , то есть плотность распределения исследуемой сети сосредоточена около точки
, то есть плотность распределения исследуемой сети сосредоточена около точки ![]() . Найдем плотность распределения отклонения от этой точки. Для этого в системе (4.1) сделаем замену переменных:
. Найдем плотность распределения отклонения от этой точки. Для этого в системе (4.1) сделаем замену переменных:![]() ,
, ![]() ,
, ![]() .
.
В новых обозначениях система (4.1) примет вид
 (4.11)
(4.11)
Систему (4.11) будем решать в три этапа.
1 этап. Устремим ![]() к нулю и обозначим
к нулю и обозначим ![]() , тогда система (4.11) перейдет в систему
, тогда система (4.11) перейдет в систему
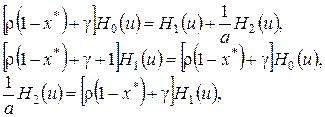 (4.12)
(4.12)
решение которой имеет вид
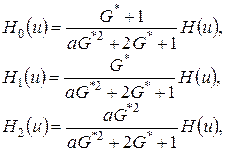 (4.13)
(4.13)
где ![]() ,
, 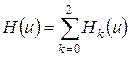 – плотность распределения нормированной величины
– плотность распределения нормированной величины ![]() отклонения процесса
отклонения процесса ![]() от значения
от значения ![]() – корня уравнения (4.10).
– корня уравнения (4.10).
Найдем вид функции ![]() .
.
2 этап. Неизвестные функции ![]() будем искать в форме
будем искать в форме
![]() (4.14)
(4.14)
где 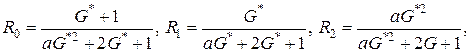 (4.15)
(4.15)
![]() – асимптотическая вероятность того, что состояние обслуживающего канала равно
– асимптотическая вероятность того, что состояние обслуживающего канала равно ![]() .
.
В системе уравнений (4.11) все функции с аргументом ![]() разложим в ряд по приращению аргумента
разложим в ряд по приращению аргумента ![]() , ограничиваясь слагаемыми порядка
, ограничиваясь слагаемыми порядка ![]() , получим
, получим
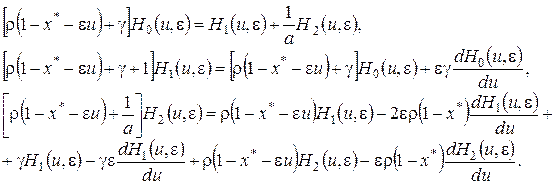 (4.16)
(4.16)
В полученных формулах заменяем ![]() по формуле (4.14), при этом учитываем, что из системы (4.12) следуют равенства
по формуле (4.14), при этом учитываем, что из системы (4.12) следуют равенства
 (4.17)
(4.17)
Получим неоднородную линейную систему алгебраических уравнений относительно неизвестных функций ![]() (в предположении, что
(в предположении, что ![]() известна) вида
известна) вида
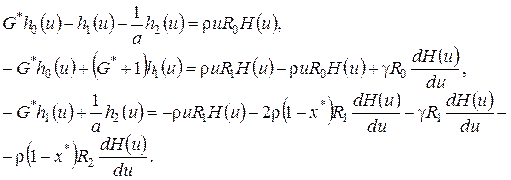 (4.18)
(4.18)
Заметим, что ранг соответствующей однородной системы равен двум. Следовательно, для того, чтобы решение системы (4.18) существовало, необходимо, чтобы ранг расширенной матрицы этой системы также равнялся двум, т.е. чтобы выполнялось следующее равенство
![]() (4.19)
(4.19)
откуда следует, что
![]() (4.20)
(4.20)
Чтобы показать равенство (4.20) воспользуемся определением для ![]() и свойствами констант
и свойствами констант ![]() , получим
, получим
 (4.21)
(4.21)
Если предположить, что функция ![]() известна, то решение системы (4.18) примет вид
известна, то решение системы (4.18) примет вид
 (4.22)
(4.22)
3 этап. В системе (4.11) все функции с аргументом ![]() разложим в ряд по приращению аргумента
разложим в ряд по приращению аргумента ![]() , ограничиваясь слагаемыми порядка
, ограничиваясь слагаемыми порядка ![]() , будем иметь
, будем иметь
![]()
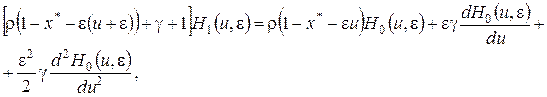 (4.23)
(4.23)

Сложив левые и правые части системы уравнений (4.23) получим
 (4.24)
(4.24)
Чтобы сделать предельный переход в полученной формуле, нужно чтобы все слагаемые имели порядок ![]() . Заменим
. Заменим ![]() по формуле (4.14), подставив вместо
по формуле (4.14), подставив вместо ![]() их выражения, полученные на втором этапе. Для
их выражения, полученные на втором этапе. Для ![]() получим линейное дифференциальное уравнение второго порядка вида
получим линейное дифференциальное уравнение второго порядка вида
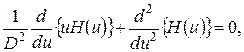 (4.25)
(4.25)
где
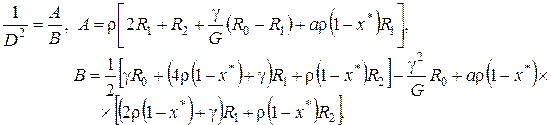 (4.26)
(4.26)
Решение уравнения (4.25) можно найти в виде
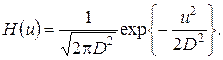 (4.27)
(4.27)
В редких случаях удается получить численное решение системы конечно-разностных уравнений для распределения случайного процесса ![]() . В силу конечности числа АС это удается сделать.
. В силу конечности числа АС это удается сделать.
Рассмотрим систему уравнений (4.1) и выпишем недостающие граничные условия для ![]() ,
, ![]() ,
, ![]() .
.
1. Рассмотрим варианты того, как в момент времени ![]() можно оказаться в состоянии
можно оказаться в состоянии ![]() :
:
а) пусть в момент времени ![]() система находится в состоянии
система находится в состоянии ![]() , то есть прибор обслуживает заявку и в ИПВ пусто. За время
, то есть прибор обслуживает заявку и в ИПВ пусто. За время ![]() с вероятностью
с вероятностью ![]() закончится обслуживание, и система окажется в состоянии
закончится обслуживание, и система окажется в состоянии ![]() ;
;
б) пусть в момент времени ![]() система находится в состоянии
система находится в состоянии ![]() , то есть прибор простаивает и в ИПВ пусто, с вероятностью
, то есть прибор простаивает и в ИПВ пусто, с вероятностью ![]() за время
за время ![]() не поступят заявки, и состояние системы не изменится.
не поступят заявки, и состояние системы не изменится.
2. Рассмотрим варианты того, как в момент времени ![]() можно оказаться в состоянии
можно оказаться в состоянии ![]() :
:
а) пусть в момент времени ![]() система находится в состоянии
система находится в состоянии ![]() , то есть прибор обслуживает заявку и в ИПВ одна заявка. За время
, то есть прибор обслуживает заявку и в ИПВ одна заявка. За время ![]() с вероятностью
с вероятностью ![]() закончится обслуживание, и система окажется в состоянии
закончится обслуживание, и система окажется в состоянии ![]() ;
;
б) пусть в момент времени ![]() система находится в состоянии
система находится в состоянии ![]() , то есть прибор простаивает и в ИПВ одна заявка, с вероятностью
, то есть прибор простаивает и в ИПВ одна заявка, с вероятностью 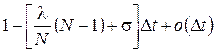 за время
за время ![]() не поступят заявки из внешнего источника и из ИПВ, и состояние системы не изменится.
не поступят заявки из внешнего источника и из ИПВ, и состояние системы не изменится.
3. Рассмотрим варианты того, как в момент времени ![]() можно оказаться в состоянии
можно оказаться в состоянии ![]() :
:
а) пусть в момент времени ![]() система находится в состоянии
система находится в состоянии ![]() , то есть прибор оповещает о конфликте и в ИПВ N заявок. За время
, то есть прибор оповещает о конфликте и в ИПВ N заявок. За время ![]() с вероятностью
с вероятностью ![]() этап оповещения о конфликте завершится, и система перейдет в состояние
этап оповещения о конфликте завершится, и система перейдет в состояние ![]() ;
;
б) пусть в момент времени ![]() система находится в состоянии
система находится в состоянии ![]() , то есть прибор простаивает и в ИПВ N заявок, с вероятностью
, то есть прибор простаивает и в ИПВ N заявок, с вероятностью ![]() за время
за время ![]() ни одна из них не обратится к прибору и состояние системы не изменится;
ни одна из них не обратится к прибору и состояние системы не изменится;
Теперь можно записать конечно-разностные уравнения
![]()
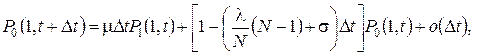 (4.28)
(4.28)
![]() ,
,
которые в стационарном режиме принимают вид
![]() ,
,
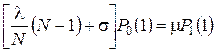 , (4.29)
, (4.29)
![]() .
.
Таким образом, для исследуемой системы мы имеем ![]() уравнения, которые имеют вид
уравнения, которые имеют вид
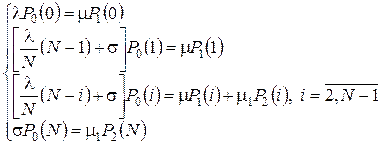 (4.30)
(4.30)
 (4.31)
(4.31)
|

Кроме того, должно выполняться условие нормировки
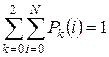 (4.33)
(4.33)
Решение системы уравнений (4.30) – (4.32), удовлетворяющее условию нормировки (4.33) можно записать следующим образом
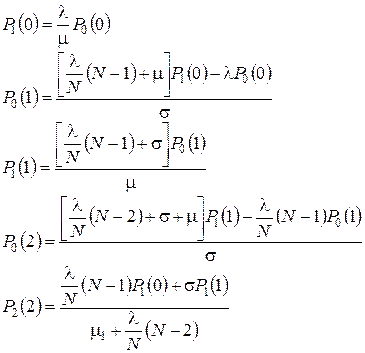 (4.34)
(4.34)

Похожие работы
... исполнители высокой квалификации; это вполне может быть осуществлено в короткие сроки силами службы эксплуатации. Использование вторичных энергоресурсов для нагрева теплоносителей в системах отопления, вентиляции и кондиционирования воздуха. Использование вторичных энергоресурсов (ВЭР) для теплоснабжения промышленных зданий приобретает все большие масштабы. Экономически это вполне оправдано – ...
... мальне значення показникунадійності, при якому приймається рішення про орєінтованийзвязок назвем порогом показника надійності і позначимо (). Для можливості порівняння результатів у різних парах змінних в одній задачі системного синтезу корисно ввести відносний показник надійності. Відносним показником надійності ηij приняття рішення про напрям звязку між змінними xj → xi (стрілка в ...



0 комментариев