Навигация
Методы минимизации функций многих переменных
1.3. Методы минимизации функций многих переменных
Критерием выбора оптимума, в нашем случае этим критерием есть выражение (1.2.1), является функция (функционал) многих переменных и для ее минимизации будем использовать наиболее известные и часто применяемые методы минимизации функций многих переменных.
В общем случае будем рассматривать задачу
![]() (1.3.1)
(1.3.1)
предполагая,
что функция
![]() непрерывно
дифференцируема
на
непрерывно
дифференцируема
на ![]() .
Согласно определению
дифференцируемости
функции
.
Согласно определению
дифференцируемости
функции
![]() (1.3.2)
(1.3.2)
где ![]() .
Если
.
Если ![]() ,
то при достаточно
малых
,
то при достаточно
малых ![]() главная часть
приращения
(1.3.2) будет определяться
дифференциалом
функции
главная часть
приращения
(1.3.2) будет определяться
дифференциалом
функции ![]() .
Справедливо
неравенство
Коши-Буняковского
.
Справедливо
неравенство
Коши-Буняковского
![]() ,
,
причем если
![]() ,
то правое неравенство
превращается
в равенство
только при
,
то правое неравенство
превращается
в равенство
только при ![]() ,
а левое неравенство
– только при
,
а левое неравенство
– только при
![]() ,
где
,
где ![]() .
Отсюда ясно,
что при
.
Отсюда ясно,
что при ![]() направление
наибыстрейшего
возрастания
функции
направление
наибыстрейшего
возрастания
функции ![]() в точке
в точке ![]() совпадает с
направлением
градиента
совпадает с
направлением
градиента ![]() ,
а направление
наибыстрейшего
убывания – с
направлением
антиградиента
,
а направление
наибыстрейшего
убывания – с
направлением
антиградиента
![]() .
.
Это замечательное свойство градиента лежит в основе ряда итерационных методов минимизации функций. Одним из таких методов является градиентный метод, к описанию которого мы переходим.
Градиентный метод. Будем считать, что некоторая точка ![]() уже выбрана. Тогда метод заключается в построении последовательности
уже выбрана. Тогда метод заключается в построении последовательности ![]() по правилу:
по правилу:

Существуют
различные
способы выбора
![]() в данном методе,
но на практике
нередко довольствуются
нахождением
какого-либо
в данном методе,
но на практике
нередко довольствуются
нахождением
какого-либо
![]() ,
обеспечивающего
условие монотонности:
,
обеспечивающего
условие монотонности:
![]() .
С этой целью
задаются какой-либо
постоянной
.
С этой целью
задаются какой-либо
постоянной
![]() и на каждой
итерации метода
берут
и на каждой
итерации метода
берут ![]() .
При этом для
каждого
.
При этом для
каждого ![]() проверяют
условие монотонности,
и в случае его
нарушения
проверяют
условие монотонности,
и в случае его
нарушения ![]() дробят до тех
пор, пока не
восстановится
монотонность
метода.
дробят до тех
пор, пока не
восстановится
монотонность
метода.
МетодНьютона. Градиентный метод является методом первого порядка, поскольку использует лишь первые производные минимизируемой функции. Однако если минимизируемая функция дважды непрерывно дифференцируема и производные вычисляются достаточно просто, то возможно применение метода минимизации второго порядка, которые используют квадратичную часть разложения этой функции в ряд Тейлора. Широко известный метод Ньютона представляет собой итерационный процесс:
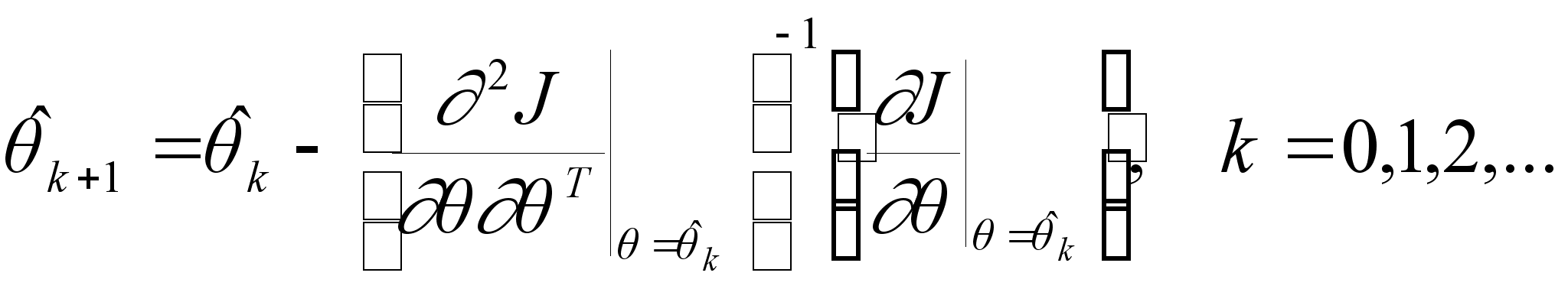
Метод сопряженных направлений. Метод сопряженных направлений является методом использующим лишь градиент функционала и описывается следующим образом:
![]() ,
,
где величина
![]() находится из
условия
находится из
условия
![]() ,
,
а ![]() вычисляется
из следующих
формул
вычисляется
из следующих
формул
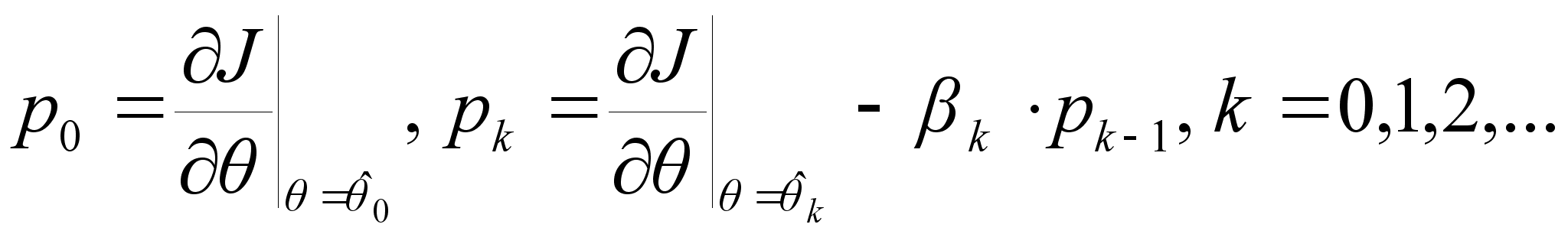
Точное определение
величины ![]() возможно лишь
в редких случаях,
поэтому реализация
каждой итерации
метода будет
сопровождаться
неизбежными
погрешностями.
Эти погрешности,
накапливаясь,
могут привести
к тому, что векторы
возможно лишь
в редких случаях,
поэтому реализация
каждой итерации
метода будет
сопровождаться
неизбежными
погрешностями.
Эти погрешности,
накапливаясь,
могут привести
к тому, что векторы
![]() перестают
указывать
направление
убывания функции,
и сходимость
метода может
нарушиться.
Чтобы бороться
с этим явлением,
метод сопряженных
направлений
время от времени
обновляют,
полагая
перестают
указывать
направление
убывания функции,
и сходимость
метода может
нарушиться.
Чтобы бороться
с этим явлением,
метод сопряженных
направлений
время от времени
обновляют,
полагая ![]() .
.
0 комментариев