Навигация
8. Програма Beeman
У програмі Вееman моделюється осцилятор Морза з допомогою алгоритму Бімана. Оскільки цей алгоритм не самостартуючий, то для всіх - числових значень х(, і використовується швидкісна форма алгоритму Верле.
PROGRAM Beeman І моделювання осцилятора Морза
CALL initialfx, v, aold, dt, dt2, nmax)
CALL energy(x, v, ecum, e2cum) 1 значення початкової енергії
CALL Verleg x, v, a, aold, dt, dt2) CALL energy{ x, v, ecum, e2cum) LET n = 1
DO whiie n < nmax
LET n = n + 1 1 число кроку
CALL Bceman{x, v, a, aold, dl, dl2)
І образування повної знергії після кожного кроку за часом CALL energY(x, v, ecum, e2cum) LOOP
CALL output{ ecum, e2cum, n) END
SUB initial( x, v, aold, dt, dt2, nmax) DECLARE DEF f LET х = 2 LET v = 0 LET aold = f(x)
INPUT prompt "крок по часу (c) = ": dt LET dt2 = dt" dt
INPUT prompt "тривалість = ": tmax LET nmax = tmax/dt END SUB
SUB Ver!et( x, v, a, aold, dt, dt2) DECLARE DEF f
LET x = x + v*dt + 0.5*ao!d*dt2 LET a = f(x)
LET v = v + 0.5"{a + ao!d)*dt END SUB
SUB Beeman(x, v, a, aold, dt, dt2) DECLARE DEF f
LET x = x + v*dt + (4*a - aold)*dt2/6
LET anew = f(x) І значення на (п+1) -му кроці LET v = v + (2*anew + 5*a - aold)*dt/6
LET aold = a значення на (n-1) -му кроці
LET а = anew значення на n-му кроці END SUB
DEF f(x) LET e = exp(- x) LET f = 2*e*(e - 1) END DEF
SUB energY(x, v, ecum, e2cuin) LET KE = 0.5*v" v LET e = exp(- x) LET PE = e*{e - 2) LET etot = KE + PE LET ecum = ecum + etot LET e2cum = e2cum + etot*etot END SUB
SUB output{ecum, e2cuiT!, n) LET n = n + 1 І вирахування початкового значення
LET ebar = ecum/n PRINT "середня енергія = ";ebar LET sigma2 = e2cum/n - ebar*ebar PRINT "sigma = "; sqr(sigma2) END SUB
Метод Адамса
Цей метод чисельного інтегрування розроблений Адамсом в 1855 році на прохання видомого англійського алтелериста Башфора, який займався внутрішньою балістикою. В подальшому цей метод був забутий і знову відкритий був норвезьким математиком Штермером. Популяризація метода Адамса і подальше його вдосконалення пов’язане із іменем Крилова.
Запишемо рівняння першого порядку
З початковими умовами  (1,2)
(1,2)
Нехай xi(i=0,1,2…)-система рівнозначних значень з кроком h i y(xi). Очевидно маємо
 (3)
(3)
В силу другої інтерполяційної формули Ньютона з точністб до різниць четвертого порядку отримуємо:
![]() (4)
(4)
де ![]() або
або ![]() (4а)
(4а)
Підставляю вираз (4а) в формулу (3) і враховуючи те, що ![]() будемо мати
будемо мати
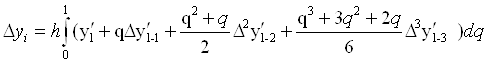
З відси отримуємо формулу експоляриціональну Адамса
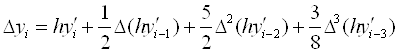 (5)
(5)
Для початкового процессу потрібно чотири початкових значення y0, y1, y2, y3, - початковий відрізок, який приділяє, виходячи із початкових умов (2), яким-небуть чисельним методом. Мажна наприклад використати метод Рунге-Кутта або розкласти в ряд Тейлора
![]()
Де i=1,2,3 (або i=-1,1,2) із відповідною зміною нумерування. Знаючи ці значення, із рівнянь (1) можна знайти значення похідних ![]() і скласти таблицю
і скласти таблицю
![]() (6)
(6)
Подальше значення yi (i=4,5…) шуканого розвязку можна крок за кроком обчислювати за формулою Адамса, поповнюючи по мірі можливості таблицю різниць (6)
Вирахувавши перше наближення для ![]() по формулі
по формулі
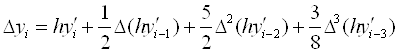
Визначити ![]() підрахувати кінцеві різниці
підрахувати кінцеві різниці
![]() (7)
(7)
а потім знайти друге наближення для більш точній формулі
![]() (8)
(8)
![]()
![]()
![]() Якщо
Якщо ![]() і
і ![]() відрізняються лишень на дкілька одиниць останнього зберігаючого десяткового розряду, то можна поставити
відрізняються лишень на дкілька одиниць останнього зберігаючого десяткового розряду, то можна поставити ![]() а потім знайшовши
а потім знайшовши ![]() перерахувавши кінцеві різниці (7). Після цього, потрібно знову знайти
перерахувавши кінцеві різниці (7). Після цього, потрібно знову знайти ![]() по формулі (8) Поту цей крок h повинен бути таким, щоб цей перерахунок був зміненим.
по формулі (8) Поту цей крок h повинен бути таким, щоб цей перерахунок був зміненим.
На практиці крок h вибирають малим, щоб можна було знехтувати членом ![]() в формулі (8)
в формулі (8)
Якщо за розбіжність величин ![]() і
і ![]() суттєва, то потрібно зменшити крок h.
суттєва, то потрібно зменшити крок h.
Звичайно крок h зменшують рівно в 2 рази. Можна показати, як в цьому випадку, маючи до деякого значення і таблицю величин хj, yj, Yj=hy’j (j<=i) з кроком ![]() , можна просто побудувати таблицю величин
, можна просто побудувати таблицю величин  з кроком
з кроком ![]()
На основі формули (4) будемо мати
![]() (9)
(9)
Де ![]() Звідси,
Звідси, ![]() і
і  і враховуючи, що
і враховуючи, що  заходимо
заходимо
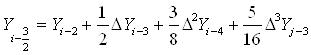 (10)
(10)
Аналогічно при ![]() із формули (9) отримаєм, що аргументу
із формули (9) отримаєм, що аргументу  відповідає значення
відповідає значення
 (11)
(11)
Що стосується значень Yi-1 i Yi, то вони знаходяться в старій таблиці. Після цього складаємо початковий відрізок для нової таблиці:
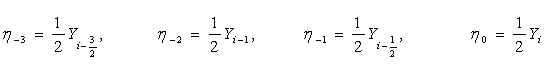
і знаходимо кінцеві різниці:
![]()

![]()

Далі таблиця будується простим способом, подальшою модифікацією формули (5):

Для роботи на компютерах формулу Адамса (5) вигідно використовувати в розкритому виді. Враховуючи, що

Після цього маємо:  причому
причому ![]()
![]()
Метод Крилова
Для спрощеня запису обмежимось розглядом диференціальних рівнянь першого порядка
![]() (1)
(1)
З початковими умовами ![]()
Введемо спочатку ряд допоміжних формул
![]()
В силу формули Адамса отримаємо
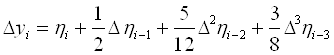 (2)
(2)
Введемо позначення ![]()
Формула (2) називається формулою похилого рядка, так як в ній використовуються різниці, які знаходяться на діагоналі таблиці різниць. Враховуючи, що ![]()
Із формули (2) будемо мати

Звідси отримуємо першу допоміжну формулу – яку ще можна назвати перша формула ламаного рядка
 (3)
(3)
Далі враховуючи, що ![]() і
і ![]() із формули (3) виводимо другу формулу – друга формула ламаного рядка
із формули (3) виводимо другу формулу – друга формула ламаного рядка
 (4)
(4)
Якщо ![]() отримаємо формулу горизонтального рядка
отримаємо формулу горизонтального рядка
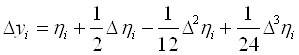 (5)
(5)
Підмітимо, що формулу (5) можна отримати безпосередньо за допомогою інтегрування, в межах від xi до xi+1розкладанням ![]() за допомогою першої інтерполяційної формули Ньютона:
за допомогою першої інтерполяційної формули Ньютона:

Перейдемо до опису метода Крилова послідовних наближень. Перше наближення полягає у тому, щоб знайти наближене значення ![]()
![]() Після цього знайдемо
Після цього знайдемо ![]() і складає різницю
і складає різницю ![]() , де
, де ![]()
![]()
![]() .
.
Значення які знайшли заносимо в розділ (І) основного бланку (таблиця 1)
Схема обчислення відрізка методом послідовних наближень
| № наближення | і | x | y |
|
|
|
|
|
| І | 0 1 | x0 x1 |
|
|
|
| ||
| ІІ | 0 1 2 | x0 x1 x2 |
|
|
|
|
| |
| ІІІ | 0 1 2 3 | x0 x1 x2 x3 |
|
|
|
|
|
|
Далі переходимо до другого наближення. Для того, використовуємо дані із знаходження ламаних рядків, обчислюємо значення ![]() і
і ![]() :
:
 (7)
(7)
 (8)
(8)
Двочленні формули отримуються відповідно із формули (5) при і=0 і із формули (2) при і=1 в результаті відкидання різниць порядка вищого ніж перший.
Таким чином, отримаємо можливість знайти
![]() і
і ![]() ,
,
в результаті чого можна порахувати
![]()
і скласти різниці
![]()
Отримані результати записуємо у таблицю в розділ 2 основного бланка
Для знаходження третього наближення застосовуємо трьохчленні формули, які отримуються із формули (2) при і=2 після відкидання різниць третього порядку. Обчислюємо значення ![]() із трьохчленних формул:
із трьохчленних формул:
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
Звідси можна знайти
![]()
і обчислити ![]()
![]()
![]() . Після цього можна заповнити розділ ІІІ в таблиці (І) знайшовши потрібні різниці звичайним порядком.
. Після цього можна заповнити розділ ІІІ в таблиці (І) знайшовши потрібні різниці звичайним порядком.
Метод Чаплигіна
Метод Чаплигіна є одним із найбільш точним із аналітичних методів наближеного інтегрування диф. рівнянь причому допускаючи просту оцінку погрішності. Суть полягає у тому, що шуканий розв’язок ![]() апроксимуючись двома послідовними функціями
апроксимуючись двома послідовними функціями
![]()
задовольняючи подвійну нерівність
![]()
і початковими умовами ![]() причому такими, що
причому такими, що ![]() на
на ![]() при
при ![]() . Геометрично це означає, що шукана інтегральна крива
. Геометрично це означає, що шукана інтегральна крива ![]() стискається в як завгодно малий криволінійний сектор А0ВnCn (мал. 1).
стискається в як завгодно малий криволінійний сектор А0ВnCn (мал. 1).
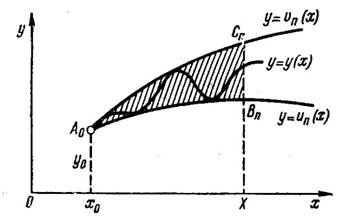 Якщо положити
Якщо положити ![]() то максимальна абсолютна погрішність наближеного розв’язку
то максимальна абсолютна погрішність наближеного розв’язку ![]() буде рівна
буде рівна ![]()
![]() ця погрішність на кожному кроці визначається безпосередньо.
ця погрішність на кожному кроці визначається безпосередньо.
Покажемо ідею метода Чаплигіна для диф. рівнянь першого порядку
![]() (1)
(1)
з початковою умовою
![]() (2)
(2)
Причому будемо мати на увазі, що права частина ![]() непереривна і має неперервні похідні
непереривна і має неперервні похідні ![]() і
і ![]() в деякому околі початкової точки
в деякому околі початкової точки ![]() . Метод побудований на одній лемі.
. Метод побудований на одній лемі.
Лема Чаплигіна про інтегральні нерівності.
Нехай ![]() - диференціальний оператор, який відповідає диференціальному рівнянню (1), і
- диференціальний оператор, який відповідає диференціальному рівнянню (1), і ![]() інтеграл рівняння (1)
інтеграл рівняння (1)
![]() (3)
(3)
яке задовольняє початкову умову ![]() і вибраний при
і вибраний при ![]() .
.
Якщо функція ![]() задовольняючи умови:
задовольняючи умови:
![]() (4)
(4)
і
![]()
то на відрізку ![]() виконується нерівність
виконується нерівність
![]() (5)
(5)
так чи однаке функція і являється наближеним розв’язком ![]() .
.
Аналогічно і для функції ![]() виконуються умови:
виконуються умови:
![]() (6)
(6)
![]()
то на відрізку ![]() має місце нерівність
має місце нерівність ![]() , (7)
, (7)
так чи однаке функція ![]() являється верхнім наближеним розв’язком
являється верхнім наближеним розв’язком ![]() у.
у.
Доведення: Достатньо доказати лиш одне із нерівностей (5) або (7). Доведемо наприклад нерівність (5). Із формул (3) і (4) маємо ![]() і
і ![]() Звіди
Звіди
![]() (8)
(8)
Де
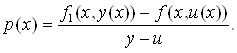 (9)
(9)
Функція ![]() втрачає зміст при х, для якого
втрачає зміст при х, для якого ![]() . В цьому випадку
. В цьому випадку

В силу наведених вище умов функція р(х) визначена і неперервна на відрізку ![]() .
.
Помножимо обидві частини диференціальної нерівності (8) на інтегруючий множник  будемо мати
будемо мати
![]() (10)
(10)
Звідси інтегруючи нерівність (10) в межах від ![]() до
до ![]() , де
, де ![]() отримаєм
отримаєм ![]() , або так як
, або так як ![]() то остаточно знаходимо
то остаточно знаходимо ![]() при
при ![]() , що і потрібно було довести.
, що і потрібно було довести.
194-Чисельні методи
Висновок:
Недоліком деяких з алгоритмів, яквляється те, що деякі з них не мають амостарту, і необхідно використовувати другий алгоритм для отримання кількох пешрих точок фазовоо простору. Недоліком алгоритму Верле полягає в тому, що нова швидкість знаходиться по формулі вираховуванням близьких по величині чисел. Така операція обумовлює втрату значущих цифр і може привести до значного збільшеня погрішності округлення.
Як вже підкреслювалося, не слід віддавати перевагу одному якому-небудь алгоритму. Успіхи в комп'ютерній технології нині дозволяють легко експерементувати з різними алгоритмами для разнообразних динамічних систем.
Список використаної літератури:
1) Х. Гулд, Я.Тобочник. Компьютерное моделирование в физике: часть1.
2) В.А.Ильина, П.К. Силаев. Численные методы для физиков-теоретиков часть2. Москва, Ижевск 2004р.
3) сайт http://uk.wikipedia.org/wiki/Метод_Рунге_—_Кутти
4) И.С. Березин, Н.П. Жидков. Методы вычислений том. 2 Москва 1959р.
5) Б.П. Демидович,И.А.Марон, З.Шувалова. Численные методы анализа. «Наука» Москва 1967р.
Похожие работы
... і, перебудову управлінської ієрархії), систем планування, контролю, оцінки діяльності персоналу, його винагороди. Подібні корінні перебудови - результат явної невідповідності стратегії і структури. Досвід внутрішньо фірмового управління 1950-1970-х років, коли жорсткість формалізованих, бюрократичних структур, очевидно, суперечила збільшеній динаміці змін зовнішнього середовища, показав, що часті ...
... коштів є важливим чинником у зниженні собівартості продукції чи виконаної роботи. Раціональне використання оборотних коштів залежить від правильного їхнього формування і ефективної організації виробництва. Зосередження н підприємствах зайвих оборотних коштів приводить до їхнього заморожування. Це завдає шкоди економіці господарства. Щоб уникнути такого положення, оборотні кошти нормуються, що є ...
... іонери. Залежно від стилю керівництва й політичної системи, в якій функціонує лідер, відрізняють: диктаторський тип, демократичний тип, автократичний тип, плутократичний тип. В сучасній політології використовується типологія М. Дж. Херманн, де за основу виступає імідж, “образ”, візуальна привабливість лідера: прапороносець, який має особистий погляд на реальність, майбутнє; чітко викладає цілі, ...
... ї моделі економіки і способів її побудови; на визначенні пріоритетних цінностей та економічного порядку, який повинен забезпечувати реалізацію цієї моделі. Тому розроблення філософії взаємодії держави і ринку передбачає дослідження багатогранності цього процесу, урахування впливу інституційного середовища на конкретну модель економіки. Без визначення цілей, цінностей у суспільстві неможливо ...







0 комментариев