Навигация
Решение уравнения методами Ньютона, Хорд
3 Решение уравнения методами Ньютона, Хорд
Метод хорд (способ пропорциональных частей) — численный метод уточнения корня трансцендентного уравнения.
Точный корень ![]() уравнения
уравнения ![]() находится на отрезке
находится на отрезке ![]() . Производная
. Производная ![]() на этом промежутке непрерывна и сохраняет постоянный знак. Приближенный корень
на этом промежутке непрерывна и сохраняет постоянный знак. Приближенный корень ![]() , при котором
, при котором ![]() , можно найти используя метод хорд. Для этого нужно взять начальное приближение корня
, можно найти используя метод хорд. Для этого нужно взять начальное приближение корня ![]() и применить к нему итерационную формулу:
и применить к нему итерационную формулу:
линейный уравнение хорда гаусс ньютон
![]() ,
, ![]() , если
, если ![]()
![]() ,
, ![]() , если
, если ![]()
Погрешность вычислений:
![]() ,
, ![]() ,
, ![]()
В отличие от метода дихотомии, обращающего внимание лишь на знаки значений функции, но не на сами значения, метод хорд использует пропорциональное деление интервала (рисунок 1).
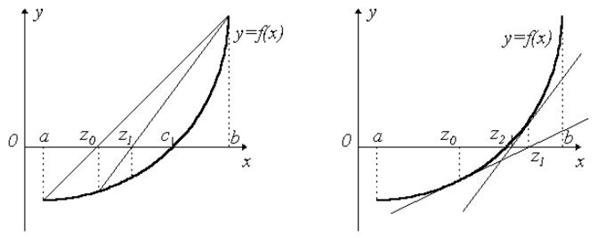
| Рис. 1. Метод хорд | Рис.2. Метод касательных |
Здесь вычисляются значения функции на концах отрезка и строится “хорда”, соединяющая точки (a, f(a)) и (b, f(b)). Точка пересечения ее с осью абсцисс
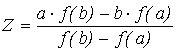
принимается за очередное приближение к корню. Анализируя знак f(z) в сопоставлении со знаком f(x) на концах отрезка, сужаем интервал до [a,z] или [z,b] и продолжаем процесс построения хорд до тех пор, пока разница между очередными приближениями не окажется достаточно малой (в пределах допустимой погрешности) |Zn-Zn-1|<![]() .
.
Можно доказать, что истинная погрешность найденного приближения:
![]() ,
,
Метод Ньютона
Пусть корень уравнения ![]() отделен на отрезке [a, b], причем
отделен на отрезке [a, b], причем ![]() и
и ![]() непрерывны и сохраняют определенные знаки при
непрерывны и сохраняют определенные знаки при ![]() . Если на некотором произвольном шаге n найдено приближенное значение корня
. Если на некотором произвольном шаге n найдено приближенное значение корня ![]() , то можно уточнить это значение по методу Ньютона. Положим
, то можно уточнить это значение по методу Ньютона. Положим
|
| (1) |
где ![]() считаем малой величиной. Применяя формулу Тейлора, получим:
считаем малой величиной. Применяя формулу Тейлора, получим:
![]()
Следовательно,
![]()
Внеся эту поправку в формулу (1), найдем следующее (по порядку) приближение корня
|
| (2) |
Геометрически метод Ньютона эквивалентен замене дуги кривой ![]() касательной, проведенной в некоторой точке кривой. В самом деле, положим для определенности, что
касательной, проведенной в некоторой точке кривой. В самом деле, положим для определенности, что ![]() при
при ![]() и
и ![]() (см. рис.).
(см. рис.).
Выберем, например, ![]() , для которого
, для которого ![]() . Проведем касательную к кривой
. Проведем касательную к кривой ![]() в точке B0 с координатами
в точке B0 с координатами![]() .
.
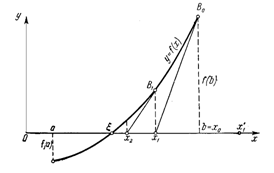
В качестве первого приближения ![]() корня возьмем абсциссу точки пересечения касательной с осью Ox. Через точку
корня возьмем абсциссу точки пересечения касательной с осью Ox. Через точку ![]() снова проведем касательную, абсцисса точки пересечения которой даст второе приближение
снова проведем касательную, абсцисса точки пересечения которой даст второе приближение ![]() корня и т.д.
корня и т.д.
Формулу для уточнения корня можно получить из прямоугольного треугольника ![]() , образованного касательной, проведенной в точке
, образованного касательной, проведенной в точке ![]() , осью абсцисс и перпендикуляром, восстановленным из точки
, осью абсцисс и перпендикуляром, восстановленным из точки ![]() .
.
Имеем ![]()
Так как угол образован касательной и осью абсцисс, его тангенс численно равен величине производной, вычисленной в точке, соответствующей абсциссе точки касания, т.е. ![]()
![]() Тогда
Тогда ![]()
или для любого шага n
![]() .
.
В качестве начальной точки ![]() можно принять либо один из концов отрезка [a, b], либо точку внутри этого интервала. В первом случае рекомендуется выбирать ту границу, где выполняется условие
можно принять либо один из концов отрезка [a, b], либо точку внутри этого интервала. В первом случае рекомендуется выбирать ту границу, где выполняется условие
![]()
т.е. функция и ее вторая производная в точке ![]() должны быть одного знака.
должны быть одного знака.
В качестве простейших условий окончания процедуры уточнения корня рекомендуется выполнение условия
![]()
Как следует из последнего неравенства, требуется при расчете запоминать три значения аргумента ![]() . В практических инженерных расчетах часто применяют сравнение аргументов на текущей и предыдущей итерациях:
. В практических инженерных расчетах часто применяют сравнение аргументов на текущей и предыдущей итерациях:
![]()
При составлении программы решения уравнения методом Ньютона следует организовать многократный расчет приближений ![]() для корня. Если удается получить аналитическое выражение для производной, то ее вычисление, а также вычисление
для корня. Если удается получить аналитическое выражение для производной, то ее вычисление, а также вычисление ![]() можно оформить в виде функций.
можно оформить в виде функций.
4 Разработка блок схемы решения системы уравнения методом Гаусса
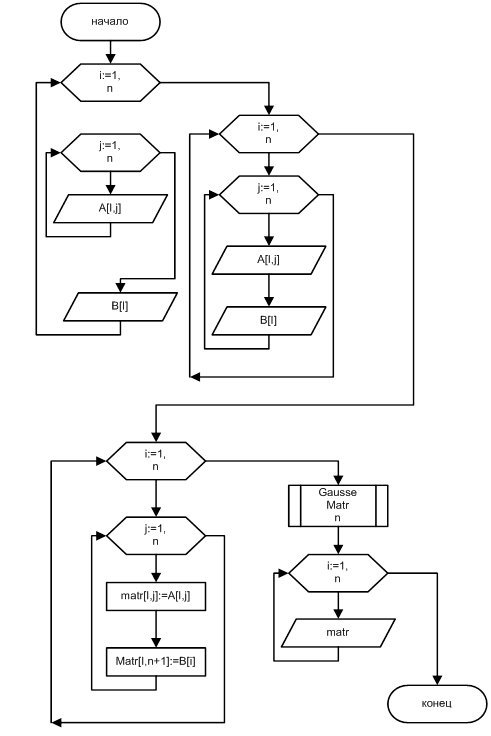
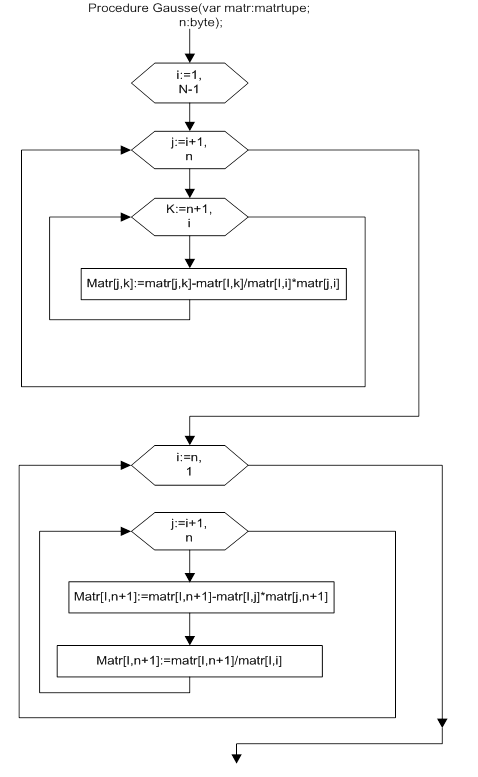
5 Разработка блок схемы решения уравнения методом Ньютона
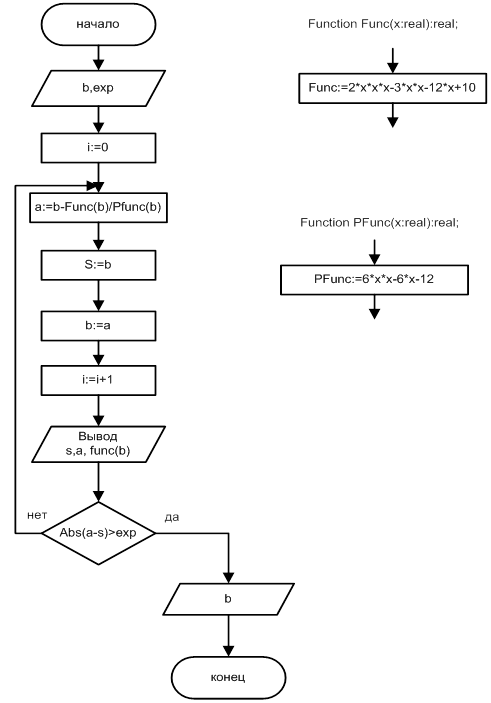
6 Разработка блок схемы решения уравнения методом Хорд

7 Язык программирования Turbo Pascal
Turbo Pascal является реализацией Pascal'я. Самая первая версия Pascal быля разработана на кафедре информатики Стэндфордского университета швейцарским ученым Николаусом Виртом в 1968 году.
С момента появления Pascal на рынке продуктов прошло много времени прежде чем он получил всеобщее признание. В середине 80-х годов американской фирмой Borland International, Inc была создана реализация языка Pascal, известная и по сей день под именем Turbo Pascal. Эта фирма объединила очень быстрый компилятор с редактором текста и добавила к стандартному Паскалю мощное расширение, что способствовало успеху первой версии этого языка.
В 1985 году на рынке ПЭВМ появился язык программирования Турбо Паскаль (версия 3.0) с компилятором стандартного Паскаля. С тех пор Паскаль стал применяться в общеобразовательных, профессионально-технических школах и в сфере высшего образования в качестве «первого» языка программирования. Благодаря простоте использования язык Турбо Паскаль получил широкое распространение и в любительских кругах. Повышению популярности Турбо Паскаля способствовал набор небольших сопутствующих программ (Toos), позволяющих получать чрезвычайно компактную, быструю и легко читаемую программу. Эти качества Турбо Паскаля были высоко оценены и в среде профессиональных программистов. Встроенный редактор текста использует достаточно широко распространенную систему команд, берущую начало от пакета WordStar и хорошо знакомую каждому, кто интенсивно использует ПЭВМ.
В появившемся со временем пакете Турбо Паскаль 4.0 было устранено большинство подвергавшихся критике ограничений компилятора и была повышена производительность системы. Кроме того, новый компилятор версии 4.0 имел существенные отличия от предыдущей версии. Наиболее важным нововведением была ИNIТ-концепция, заимствованная из языка Модула-2. Это дало возможность реализовать в рамках ТП разработку крупных программных продуктов.
С выходом в свет версии 5.0 ТП получил еще большие шансы на благосклонную реакцию со стороны профессиональных пользователей благодаря встроенному в среду программирования интегрированному отладчику, который позволил повысить производительность труда.
Существенно улучшила технические характеристики ТП реализация аппарата перекрытий (overlays), позволяющего строить мощные программные комплексы, рассчитанные на эксплуатацию в малых по объему областях памяти. Суть механизма перекрытий сводится к делению программы на части, поочередно загружаемые по мере необходимости с дискеты или жесткого диска в одну и ту же область памяти, заменяя при этом находившуюся там часть программы.
Кроме того, в ТП 5.0 были расширены возможности отладки программ и обеспечена возможность поддержки расширенной памяти в стандарте Lotus-Intel-Microsoft (SLIMS/EMS 4.0). Сокращение EMS обозначает Expanded Memory Specification (спецификация расширенной памяти). Нельзя путать этот вид дополнительной памяти с другим — Extended Memory. EMS имеется на обычных ПЭВМ класса XT, в то время как Extended Memory — только на машинах АТ-класса (с процессором 286, 386 и выше) при объеме памяти свыше 1 Мбайта.
В этой версии были также исправлены и улучшены библиотеки графических процедур, поставляемые вместе с пакетом ТП и обеспечивающие полную совместимость с графическими адаптерами класса VGA (Video Graphics Array).
В рамках версии ТП 5.5 были осуществлены дальнейшие преобразования в направлении улучшения технических характеристик пакета. Наряду с внутренними улучшениями и новыми возможностями встроенной справочной системы Help, а также большим набором учебных примеров, важным нововведением явилась реализация в языке концепции объектно-ориентированного программирования (ООП).
Через некоторое время на рынке появился ТП 6.0, в котором теоретическая концепция объектно-ориентированного программирования была реализована практически с полным набором объектов, которые могли использоваться для решения прикладных задач. Кроме того, реализация системы меню приведена в соответствие со стандартом SAA (Turbo Vision). В качестве практического примера использования новых возможностей был реализован текстовый редактор, встроенный в IDE ~ Integrated Development Environment — интегрированную инструментальную оболочку. При этом сторонники программирования на ТП 6.0 получили возможность не только работать со встроенным многооконным текстовым редактором, но и использовать мышь, которая значительно облегчает работу пользователя.
В 1992 году фирма Borland International представила пользователям очередную версию языка Паскаль — Турбо Паскаль 7.0. Наряду со всеми преимуществами, которые унаследованы от предыдущей версии (многооконный режим работы, возможность использования мыши, возможность использования языка программирования низкого уровня Ассемблер, возможность создавать объектно-ориентированные программы), в ТП 7.0 были произведены изменения и улучшения. Во-первых: появилась возможность выделять определенным цветом различные элементы исходного текста (зарезервированные слова, идентификаторы, числа и т. д.), позволяющая даже неопытным пользователям устранять ошибки на этапе ввода исходного текста. Во-вторых: язык программирования ТП 7.0 был расширен (появилась возможность использовать типизированный адресный оператор, открытые массивы и строки и т. д.), что предоставило пользователю дополнительные возможности при решении повседневных задач. В-третьих: был улучшен компилятор, вследствие чего «коды программ» стали более эффективными. В-четвертых: был улучшен интерфейс пользователя. Кроме того, в ТП 7.0 расширены возможности объектно-ориентированного программирования (в частности, расширены и улучшены возможности Turbo Vision).
8 Разработка программы решения системы уравнения методом Гаусса при помощи Turbo Pascal
program Gauss;
const
N=3;
A:array[1..N,1..N] of real = ((9.1, 5.6, 7.8),
(3.8, 5.1, 2.8),
(4.1, 5.7, 1.2));
B:array[1..N] of real = (9.8,
6.7,
5.8);
type
matrtype=array[1..N,1..N+1] of real;
var
i,j:byte;
matr:matrtype;
procedure Gausse(var matr:matrtype; N:byte);
var i,j,k:byte;
begin
for i:=1 to N-1 do
for j:=i+1 to N do
for k:=N+1 downto i do
matr[j,k]:=matr[j,k]-matr[i,k]/matr[i,i]*matr[j,i];
for i:=N downto 1 do
begin
for j:=i+1 to N do
Matr[i,N+1]:=Matr[i,N+1]-Matr[i,j]*Matr[j,N+1];
Matr[i,N+1]:=Matr[i,N+1]/Matr[i,i];
end;
end;
begin
clrscr;
writeln('reshenie sistemi iz ',N,' linear yravnenii');
for i:=1 to N do
begin
writeln('vvodim yravnenie',i,':');
for j:=1 to N do
begin
write('A[',i
,',',j,']=');
read(A[i,j]);
end;
write('B[',i,']=');
readln(B[i]);
end;
writeln('Sistema linear yravnenii');
for i:=1 to N do
begin
for j:=1 to N do
write(A[i,j]:5:2);
writeln(B[i]:5:2);
end;
for i:=1 to N do
begin
for j:=1 to N do
matr[i,j]:=A[i,j];
matr[i,N+1]:=B[i];
end;
Gausse(matr,N);
writeln('reshenie sistemi yravnenii:');
for i:=1 to N do
writeln('X',i,'=',matr[i,N+1]:5:2);
readkey;
end.
9 Разработка программы решения уравнения методом Ньютона при помощи Turbo Pascal
uses crt;
var
a,b,Exp,s : real;
i : integer;
function Func(x : real) : real;
begin
Func:=2*x*x*x-3*x*x-12*x+10;
end;
function PFunc(x : real) : real;
begin
PFunc:=6*x*x-6*x-12;
end;
Begin
clrscr;
Writeln('Vvedite verhnij predel:');
readln(b);
Writeln('Vvedite to4nost'':');
readln(Exp);
i:=0;
repeat
a:=b-Func(b)/PFunc(b);
s:=b;
b:=a;
i:=i+1;
Writeln('Shag ',s:5:2,' X-',a:5:2,' f(x)=',Func(b));
until(abs(a-s)>Exp);
Writeln('Otvet: ',b:5:2);
readln;
end.
10 Разработка программы решения уравнения методом Хорд при помощи Turbo Pascal
program hord;
var x,a,b,eps,s:real;
function f(x:real):real;
begin
f:=2*x*x*x-3*x*x-12*x+10;
end;
begin
write('vvedite levuiu granicu');
readln(a);
write('vvedite pravuiu granicu');
readln(b);
write('vvedite epsilon');
readln(eps);
while f(b)-f(a)>=eps do
begin
s:=b-f(b)/(f(b)-f(a))/(b-a);
a:=b; b:=s;
end;
writeln(s:5:2);
readln;
end.
Заключение
В соответствии с заданием курсовой работы была осуществлена программная реализация задачи. В ходе выполнения работы были получены навыки программирования системы уравнений.
Список используемых источников
1) Блашкин И.И., Буров А.А. Новые возможности Turbo-Pascal 7.1. — Спб.: Изд-во “Макет”, 2005.
2) Бородич Ю.С. и др. Паскаль для персональных компьютеров: Справ. Пособие/ Ю.С. Бородич, А.Н. Вальвачев, А.И.Кузьмич. — Мн.: Выш. Шк.: БФ ГИТМП “НИКА”, 2001.
3)Васильев П.П. Турбо Паскаль — мой друг: М.: Компьютер, ЮНИТИ, 2006.
4) Джордейн Р. Справочник программиста персональных компьютеров типа IBM PC, XT, AT: Пер. с англ./ Предисл. Н.В. Гайского. — М.: Финансы и статистика, 2001.
5) Зуев Е.А. Язык программирования Turbo Pascal 7.1. — М.: Унитех, 2005.
Похожие работы
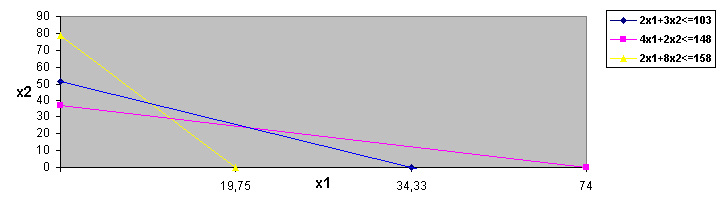
... а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке. Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок у(у1, y2, y3) минимизирующий общую оценку всех ресурсов f = 103у1 + 148у2 + 158у3 (1) при условии, что по каждому виду ...
... , является линейной функцией переменных : (2.4) Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) найти решение, минимизирующее линейную функцию (2.4). Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без ...
... данных будет нести больше смысла, если его отсортировать каким‑либо образом. Часто требуется сортировать данные несколькими различными способами. Во‑вторых, многие алгоритмы сортировки являются интересными примерами программирования. Они демонстрируют важные методы, такие как частичное упорядочение, рекурсия, слияние списков и хранение двоичных деревьев в массиве. Наконец, сортировка ...
... поставленной задачи. 1. Постановка задачи Для формирования четкого представления о предложенном методе необходимо подробно рассмотреть предметную область, а именно, параметрический анализ структуры Тьюринга [2]. В общем случае под термином структура Тьюринга понимают систему дифференциальных уравнений определенного вида. Для реакции двух веществ с одномерной диффузией система уравнений будет ...
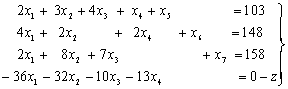
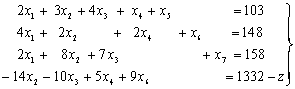
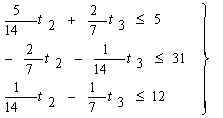
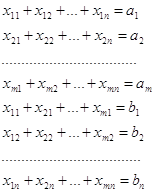
0 комментариев