Навигация
Программирование системы уравнений
Содержание
Введение
1 Постановка задачи
2 Решение системы уравнения методом Гаусса
3 Решение уравнения методами Ньютона, Хорд
4 Разработка блок схемы решения системы уравнения методом Гаусса
5 Разработка блок схемы решения уравнения методом Ньютона
6 Разработка блок схемы решения уравнения методом Хорд
7 Язык программирования Turbo Pascal
8 Разработка программы решения системы уравнения методом Гаусса при помощи Turbo Pascal
9 Разработка программы решения уравнения методом Ньютона при помощи Turbo Pascal
10 Разработка программы решения уравнения методом Хорд при помощи Turbo Pascal
Заключение
Список используемых источников
Введение
В основе того или иного языка программирования лежит некоторая руководящая идея, оказывающая существенное влияние на стиль соответствующих программ.
Исторически первой была идея структурирования программ, в соответствии с которой программист должен был решить, какие именно процедуры он будет использовать в своей программе, а затем выбрать наилучшие алгоритмы для реализации этих процедур. Появление этой идеи было следствием недостаточной изученности алгоритмической стороны вычислительных процессов, столь характерной для ранних программных разработок (сороковые — пятидесятые годы). Типичным примером процедурно-ориентированного языка является Фортран – первый и всё ещё один из наиболее популярных языков программирования. Последовательное использование идеи процедурного структурирования программ привело к созданию обширных библиотек программирования, содержащих множество сравнительно небольших процедур, из которых, как из кирпичиков, можно строить «здание» программы.
По мере прогресса в области вычислительной математики акцент в программировании стал смещаться с процедур в сторону организации данных. Оказалось, что эффективная разработка сложных программ нуждается в действенных способах контроля правильности использования данных. Контроль должен осуществляться как на стадии компиляции, так и при прогоне программ, в противном случае, как показала практика, резко возрастают трудности создания крупных программных проектов. Отчётливое осознание этой проблемы привело к созданию Ангола-60, а позже Паскаля, Модулы-2, Си и множества других языков программирования, имеющих более или менее развитые структуры типов данных. Логическим следствием развития этого направления стал модульный подход к разработке программ, характеризующийся стремлением «спрятать» данные и процедуры внутри модуля.
Начиная с языка Симула-67, в программировании наметился новый подход, который получил название объектно-ориентированного программирования (в дальнейшем ООП). Его руководящая идея заключается в стремлении связать данные с обрабатывающими эти данные процедурами в единое целое – объект. Характерной чертой объектов является инкапсуляция (объединение) данных и алгоритмов их обработки, в результате чего и данные, и процедуры во многом теряют самостоятельное значение.
1 Постановка задачи
Цель решения задачи курсовой работы – автоматизация решения системы уравнения методом Гаусса, а так же решения уравнения методами Хорд и Ньютона.
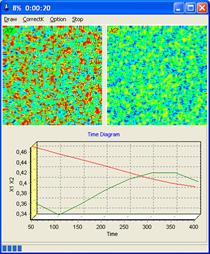
Выходная информация задачи выводиться на экран монитора.
Входная информация задачи поступает путем ввода пользователем данных для решения поставленной задачи
Прекращение решения задачи выполняется при выходе нового программного обеспечения, связанного с решением данной задачи или появление новой версии данного продукта.
2 Решение системы уравнения методом Гаусса
Метод Гаусса— классический метод решения системы линейных алгебраических уравнений (СЛАУ). Состоит в постепенном понижении порядка системы и исключении неизвестных.
Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К. Ф. Гаусса. Первое известное описание данного метода — в китайском трактате «Математика в девяти книгах», составленном между I в. до н.э. и II в. н. э.
Описание методаПусть исходная система выглядит следующим образом
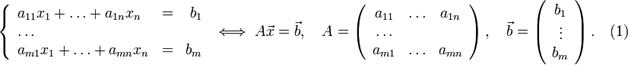
Тогда согласно свойству элементарных преобразований над строками эту систему можно привести к ступенчатому виду:
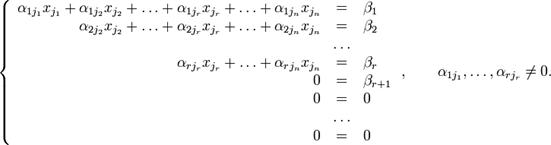
Переменные ![]() называются главными переменными. Все остальные называются свободными.
называются главными переменными. Все остальные называются свободными.
Если ![]() , то рассматриваемая система несовместна.
, то рассматриваемая система несовместна.
Предположим, что ![]() .
.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом ![]() (
(![]() , где
, где ![]() — номер строки):
— номер строки):
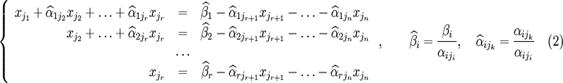 ,
,
где ![]()
Если свободным переменным системы (2) придавать все возможные значения и вычислить через них главные переменные, то мы получим все решения. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях полученное нами решение является решением системы (1).
Следствия:
1: Если в совместной системе все переменные главные, то такая система является определённой.
2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной. Условие совместности.Упомянутое выше условие ![]() может быть сформулировано в качестве необходимого и достаточного условия совместности:
может быть сформулировано в качестве необходимого и достаточного условия совместности:
Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
1) На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получавшуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
2) На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
В простейшем случае алгоритм выглядит так:
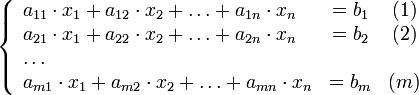
· Прямой ход:
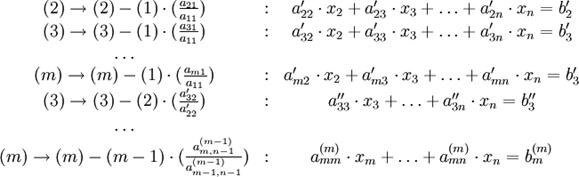
3) Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для:
1) нахождения матрицы, обратной к данной (к матрице справа приписывается единичная такого же размера, что и исходная: ![]() , после чего
, после чего ![]() приводится к виду единичной матрицы методом Гаусса—Жордана; в результате на месте изначальной единичной матрицы справа оказывается обратная к исходной матрица:
приводится к виду единичной матрицы методом Гаусса—Жордана; в результате на месте изначальной единичной матрицы справа оказывается обратная к исходной матрица: ![]() );
);
2) определения ранга матрицы (согласно следствию из теоремы Кронекера—Капелли ранг матрицы равен числу её главных переменных);
3) численного решения СЛАУ в вычислительной технике (ввиду погрешности вычислений используется Метод Гаусса с выделением главного элемента, суть которого заключена в том, чтобы на каждом шаге в качестве главной переменной выбирать ту, при которой среди оставшихся после вычёркивания очередных строк и столбцов стоит максимальный по модулю коэффициент).
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Система т линейных уравнений с п неизвестными имеет вид:
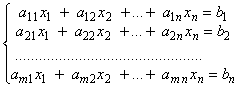
x1 , x2, …, xn – неизвестные.
aij- коэффициенты при неизвестных.
bi - свободные члены (или правые части)
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными, если они имеют одно и то же множество решений.
К элементарным преобразованиям системы отнесем следующее:
1) перемена местами двух любых уравнений;
2) умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
3) прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Элементарные преобразования переводят систему уравнений в равносильную ей.
Элементарные преобразования системы используются в методе Гаусса.
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
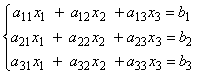 ( 1 )
( 1 )
1-ый шаг метода Гаусса.
На первом шаге исключим неизвестное х1 из всех уравнений системы (1), кроме первого. Пусть коэффициент ![]() . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а11. Получим уравнение:
. Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а11. Получим уравнение:
![]() ( 2 )
( 2 )
где ![]()
Исключим х1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х1 (соответственно а21 и а31).
Система примет вид:
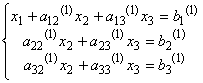 ( 3 )
( 3 )
Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.
2-ой шаг метода Гаусса.
На втором шаге исключим неизвестное х2 из третьего уравнения системы (3). Пусть коэффициент ![]() . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:
. Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:
![]() ( 4 )
( 4 )
где 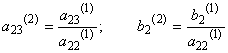
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на ![]() Получим уравнение:
Получим уравнение: ![]()
Предполагая, что ![]() находим
находим 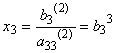
В результате преобразований система приняла вид:
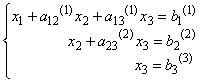 (5)
(5)
Система вида (5) называется треугольной.
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х3 подставляют во второе уравнение системы (5) и находят х2. Затем х2 и х3 подставляют в первое уравнение и находят х1.
В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.
Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.
Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b ¹ 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
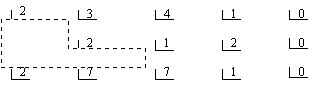
Треугольная система имеет вид:
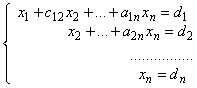
Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.
Ступенчатая система имеет вид:
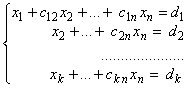
Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными хk+1, … , xk переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х1, … , xk, которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.
Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.
Похожие работы
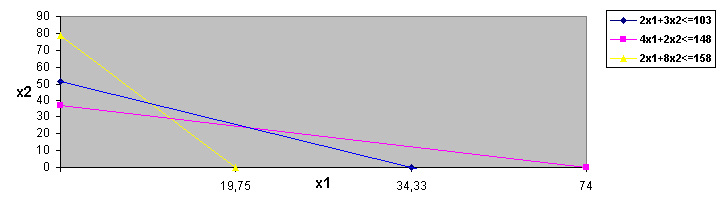
... а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке. Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок у(у1, y2, y3) минимизирующий общую оценку всех ресурсов f = 103у1 + 148у2 + 158у3 (1) при условии, что по каждому виду ...
... , является линейной функцией переменных : (2.4) Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) найти решение, минимизирующее линейную функцию (2.4). Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без ...
... данных будет нести больше смысла, если его отсортировать каким‑либо образом. Часто требуется сортировать данные несколькими различными способами. Во‑вторых, многие алгоритмы сортировки являются интересными примерами программирования. Они демонстрируют важные методы, такие как частичное упорядочение, рекурсия, слияние списков и хранение двоичных деревьев в массиве. Наконец, сортировка ...
... поставленной задачи. 1. Постановка задачи Для формирования четкого представления о предложенном методе необходимо подробно рассмотреть предметную область, а именно, параметрический анализ структуры Тьюринга [2]. В общем случае под термином структура Тьюринга понимают систему дифференциальных уравнений определенного вида. Для реакции двух веществ с одномерной диффузией система уравнений будет ...
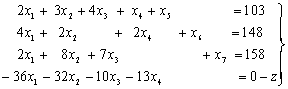
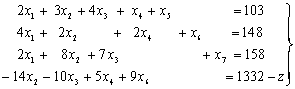
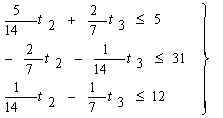
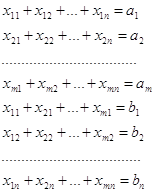
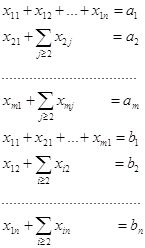
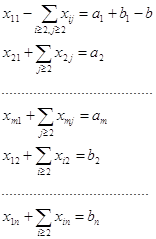
0 комментариев