Навигация
Дисциплина: «Высшая математика»
Тема: «Несобственные интегралы»
1. Несобственные интегралы с бесконечными пределами
При введении понятия определенного интеграла, а также при рассмотрении задач, связанных с ним, все время делалось предположение, что область интегрирования конечна, а интегрируемая функция на нем непрерывна. Если интервал интегрирования бесконечен или функция в этом интервале имеет точки разрыва, то введенное выше понятие определенного интеграла неприменимо. Однако существует целый ряд задач, когда возникает необходимость распространить понятие определенного интеграла на случаи бесконечных интервалов интегрирования и разрывных функций.

Рассмотрим вначале случай интегралов с бесконечными пределами. Пусть функция ![]() непрерывна на промежутке
непрерывна на промежутке ![]() . Следовательно, можно вычислить любой определенный интеграл с верхним пределом
. Следовательно, можно вычислить любой определенный интеграл с верхним пределом ![]() . Величина этого интеграла будет меняться в процессе изменения
. Величина этого интеграла будет меняться в процессе изменения ![]() , но его можно будет вычислить до тех пор, пока
, но его можно будет вычислить до тех пор, пока ![]() конечное число. Как только верхний предел станет равным бесконечности,
конечное число. Как только верхний предел станет равным бесконечности, ![]() -ая интегральная сумма, приводящая в пределе к определенному интегралу, потеряет смысл. Действительно, в этом случае уже нельзя будет ни задать
-ая интегральная сумма, приводящая в пределе к определенному интегралу, потеряет смысл. Действительно, в этом случае уже нельзя будет ни задать ![]() , ни вычислить
, ни вычислить ![]() . Иначе говоря, последняя частичная трапеция при записи
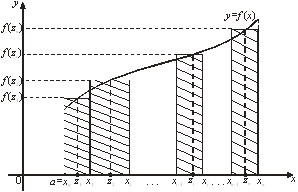
. Иначе говоря, последняя частичная трапеция при записи ![]() -ой интегральной суммы будет всегда иметь бесконечно большое основание и ее площадь вычислить обычными методами не удастся. В этом случае выход из положения заключается в том, что
-ой интегральной суммы будет всегда иметь бесконечно большое основание и ее площадь вычислить обычными методами не удастся. В этом случае выход из положения заключается в том, что ![]() находится не на бесконечности, а стремится к ней.
находится не на бесконечности, а стремится к ней.
Определение 1. Если существует конечный предел 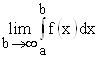 , то этот предел называется несобственным интегралом с бесконечным пределом от функции
, то этот предел называется несобственным интегралом с бесконечным пределом от функции ![]() и обозначается
и обозначается 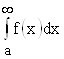 .
.
Итак, по определению 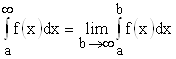 . В этом и заключается метод вычисления таких интегралов. Очевидно, что поскольку данное вычисление связано с нахождением предела, то ответ может существовать или нет.
. В этом и заключается метод вычисления таких интегралов. Очевидно, что поскольку данное вычисление связано с нахождением предела, то ответ может существовать или нет.
Определение 2. Если в несобственном интеграле предел существует, то интеграл называется сходящимся, если предел не существует или равен бесконечности, то интеграл называется расходящимся.
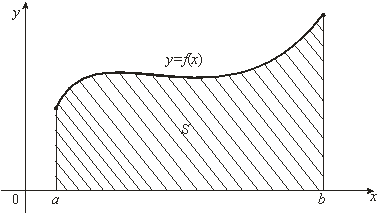
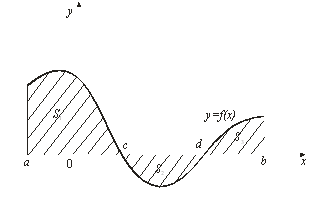
Очевидно, с геометрической точки зрения несобственный интеграл с бесконечными пределами равен площади неограниченной области, лежащей между осью ![]() , кривой
, кривой ![]() и прямой
и прямой ![]() .
.
Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:
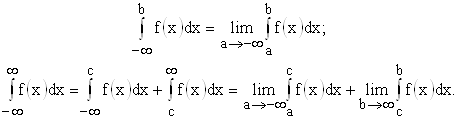
Следует подчеркнуть, что интеграл 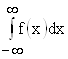 существует только тогда, когда существует каждый из интегралов
существует только тогда, когда существует каждый из интегралов 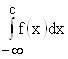 и
и 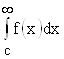 .
.
Из сказанного выше следует, что несобственный интеграл это не предел интегральной суммы, а предел определенного интеграла с переменным верхним пределом интегрирования.
Рассмотрим пример вычисления несобственного интеграла с бесконечным пределом, который, кроме того, применяется и при решении других задач, о чем будет сказано в дальнейшем.
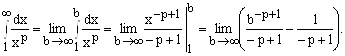
Если ![]() , то
, то ![]() , поэтому
, поэтому 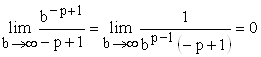 . Следовательно, в этом случае
. Следовательно, в этом случае 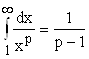 .
.
Если ![]() , то
, то ![]() , поэтому
, поэтому 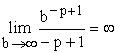 и
и 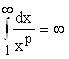 . Аналогично, если
. Аналогично, если ![]() , то
, то 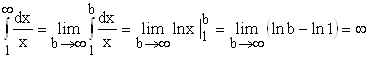 .
.
Таким образом, ![]() сходится, если
сходится, если ![]() и расходится, если
и расходится, если ![]() .
.
Несобственные интегралы с бесконечными пределами имеют место, в частности, в физике при вычислении работы по перемещению материальной точки с массой ![]() из бесконечности в точку
из бесконечности в точку ![]() под действием силы притяжения. Эта работа называется потенциалом силы притяжения материальной точки
под действием силы притяжения. Эта работа называется потенциалом силы притяжения материальной точки ![]() при
при ![]() .
.
Похожие работы
... Решение. Этот интеграл расходится, так как подынтегральная функция f(х)~. Но Следовательно, этот интеграл существует в смысле главного значения и (p.) Собственные интегралы, зависящие от параметра Пусть f: [а; b] х Y → R, где [а; b] R, Y- любое множество, а [а; b] х Y = {(х, у): х [а; b], уY}. Предположим, что функция f интегрируема по Риману на отрезке [а; b]. Определение 2.7 ...
... его тождество. Общим решением дифференциального уравнения го порядка называется такое его решение , которое является функцией переменных и произвольных независимых постоянных . Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных . Теорема. Пусть в дифференциальном уравнении (1) функция ...
... выражением, – переменной интегрирования; отрезок называется промежутком интегрирования. Теорема 1. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке. 2. Геометрический смысл определенного интеграла Пусть на отрезке задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью ...
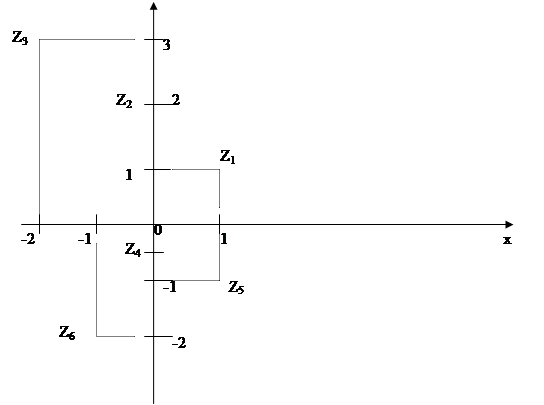
... десятичной дробью, такие как π , , и т.д. 5) комплексные числа, вводящие в рассмотрение «мнимое число» . История развития числа от целого числа до иррационального знакома нам по школьному курсу. С эпохи Возрождения математики стали использовать числа вида z = x+iy для решения квадратных уравнений, дискриминант у которых отрицателен, где i =, i² = –1, х и у – вещественные числа Само ...



0 комментариев