Навигация
Построение конечного поля
21743
знака
0
таблиц
12
изображений
1.4.3 Построение конечного поля
Определение: Многочленом 
над конечным полем
называют многочлен, коэффициенты которого лежат в .
Построение порождающего полинома циклического кода напрямую связано с расширением конечного поля, рассмотрим построение расширения поля. Так как в рамках данной работы рассматриваются двоичные циклические коды, то не трудно догадаться, что основное поле Галуа будет состоять из двух элементов – нуля и единицы - GF(2). Построим расширение поля GF(24), это поле пригодно для построения циклического кода длины 15, так как 24-1 = 15. Для построения расширения поля нужно выбрать полином по модулю которого оно будет построено, исходя из того, что m = 4 необходим полином четвертой степени. Из таблицы в книге [1] или таблицы из приложения выберем полином 
. Примитивный элемент 
поля – x. Напомним, что расширение поля является мультипликативной группой примитивного элемента , в нашем случае это x, а также умножение будет проводиться по модулю неприводимого полинома . Начнем со степени элемента x равной 0.
Умножим 
на 
по модулю полинома : 
, разделим х на , остаток от деления равен х. Не будем рассматривать формирование элементов соответствующих 1-3 степеням, рассмотрим формирование элементов для степеней 4 и 5:
Рассмотрим вычисление элемента 
Рассмотрим вычисление элемента 
И так далее, пока не будет получено 24= 16 элементов. Ниже представлено представление поля GF(24), полученного способом, изложенным выше.
Таблица 1. Представление поля GF(24).
1.4.4 О корнях полиномов и минимальных полиномах
Минимальным полиномом или функцией минимума элемента
поля GF(pm) называется полином mi(x) наименьшей степени с коэффициентами из GF(p), для которого является корнем, иначе говоря, mi ()=0.
Рассмотрим теорему, которая является ключевой для построения порождающего полинома кода по последовательности корней, ее доказательство можно найти в книгах [1] и [2].
Теорема. 1. Предположим, что fi(x) над GF(p) является минимальным полиномом элемента 
из GF(pm). Тогда f(x) является также минимальным полиномом элемента
.
Определение. Два элемента из GF(pm) называются сопряженными, если они являются корнями одного и того же минимального полинома над GF(p) (это означает, что коэффициенты полинома лежат в GF(p)).
Следствие 1 теоремы 1:
Можно сделать вывод, что у элемента может быть не один сопряженный элемент, таких элементов может быть m или меньше. Используя теорему 1 можно составить последовательность сопряженных элементов, такую последовательность в литературе еще называют циклотомическим классом. Множество элементов, входящие в циклотомический класс (сопряженные элементы) можно найти по следующей формуле:
(1)
Где, С – циклотомический класс, s – степень элемента для которого находятся сопряженные элементы, p – показатель основного поля, m – число элементов расширения поля.
Рассмотрим пример нахождения циклотомического класса для элемента 
из GF(24). Здесь и далее будем представлять элемент, как его степень.
Итак, s = 1, p = 2, m = 4.
Таким образом, для элемента будут сопряженными элементы 
Следует иметь ввиду, что при построении циклотомического класса, степень элемента 
может быть выше максимальной степени, полученной при построении расширения поля, в этом случае необходимо разделить этот элемент на полином, по которому было построено расширение поля и взять остаток от деления (так как группа является циклической, см. выше). Также нужно иметь ввиду, что при построении циклотомического класса, некоторые элементы могут оказаться одинаковыми, тогда такой элемент присутствует в классе в одном экземпляре.
Следствие 2 из теоремы 1:
Два сопряженных между собой элемента будут иметь один и тот же минимальный полином.
Теорема 2. Минимальный полином элемента равен
,
где 
сопряженные элементы
Следствие из теоремы 2: Все элементы GF(pm) являются корнями полиномов.
Построим минимальный полином для элемента из GF(24). Сопряженные элементы для найдены выше.
Используя теорему 2, запишем минимальный полином в общем виде:
Теперь нужно раскрыть скобки, по обычным правилам, не приводя подобные, помня что, операция вычитания определена по правилам для поля GF(2), и она эквивалента операции сложения.
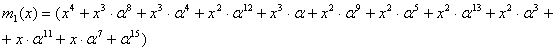
Если один из элементов имеет степень выше, чем максимальная степень элементов в таблице 1 (циклической группе), обозначим такой элемент как 
, то необходимо разделить на полином, по которому было построено расширение, и взять остаток от деления, остаток будет являться искомым элементом. Это обеспечивается тем, что мультипликативная группа примитивного элемента образует циклическую группу (см. выше).
Теперь, нужно заменить элементы разложения на элементы из GF(pm), с учетом вышесказанного, раскрыть скобки, привести подобные, не забывая, что операция сложения проводится по модулю p (в данном примере по модулю два, так как в качестве основного поля выбрано GF(2)).
Резюме: Для нахождения минимального полинома для элемента из GF(pm) необходимо:
1. Построить расширение поля по модулю некоторого неприводимого над GF(p) полинома.
2. Построить циклотомический класс для элемента , учитывая то, что одинаковые элементы в классе учитываются только один раз и то, что степень элемента класса может превышать максимальную степень элементов расширения поля.
3. При помощи теоремы 2 записать разложение минимального полинома, используя в качестве корней элементы циклотомического класса.
4. Раскрыть скобки разложения, не приводя подобные.
5. Проверить, не превышает ли степень максимальную степень элементов GF(pm) (см. выше).
6. Заменить элементы на элементы поля.
Похожие работы
... , если его длина n=qm-1 над GF(q). Если длина кода меньше длины примитивного кода, то код называется укороченным или непримитивным. Общее свойство кодовых слов циклического кода - это их делимость без остатка на некоторый многочлен g(x), называемый порождающим. Результатом деления двучлена xn+1 на многочлен g(x) является проверочный многочлен h(x). При декодировании циклических кодов используются ...
... кодов используются так называемые сверточные коды, контрольные биты, в которых формируются непрерывно из информационных и контрольных бит смежных блоков. Выводы Таким образом, в результате написания реферата, пришли к выводу, что коды Боуза-Чоудхури-Хоквингхема – это широкий класс циклических кодов, способных исправлять многократные ошибки. БЧХ-коды играют заметную роль в теории и практике ...
... ? 8. Какими программами можно воспользоваться для устранения проблем и ошибок, обнаруженных программой Sandra? Раздел 3. Автономная и комплексная проверка функционирования и диагностика СВТ, АПС и АПК Некоторые из достаточно интеллектуальных средств вычислительной техники, такие как принтеры, плоттеры, могут иметь режимы автономного тестировании. Так, автономный тест принтера запускается без ...
... мероприятия по обеспечению однородности выпускаемой продукции. Все эти мероприятия можно объединить в четыре группы: 1. совершенствование технологии производства; 2. автоматизация производства; 3. технологические (тренировочные) прогоны; 4. статистическое регулирование качества продукции. 2.10. Проектирование технологических процессов с использованием средств ...
0 комментариев