Навигация
Среди n лотерейных билетов k выигрышных. Наудачу взяли m билетов. Определить вероятность того, что среди m билетов l выигрышных
3. Среди n лотерейных билетов k выигрышных. Наудачу взяли m билетов. Определить вероятность того, что среди m билетов l выигрышных.
Дано: n = 10, l = 5, m =7 , k = 7.
Решение.
Пусть событие А - среди 7 билетов 5 выигрышных. Вероятность события А находим с помощью классического определения вероятности:
![]() ,
,
где: m – число исходов, благоприятствующих появлению события А, n – общее число равновозможных исходов испытания.
Находим m. Из 7 выигрышных билетов 5 билета можно выбрать ![]() способами, а 2 безвыигрышных билетов из 3 билетов можно выбрать
способами, а 2 безвыигрышных билетов из 3 билетов можно выбрать ![]() способами. Тогда число исходов, благоприятствующих появлению события А, используя теорему умножения, будет равно:
способами. Тогда число исходов, благоприятствующих появлению события А, используя теорему умножения, будет равно:
m = ![]() ×
×![]() =
=![]()
Находим n. . Из 10 билетов 7 билета можно выбрать ![]() способами, тогда
способами, тогда
n = ![]()
Отсюда, искомая вероятность равна:
![]()
Ответ: Р(А) = 0,525.
4. В лифт k-этажного дома сели n пассажиров (n < k). Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что: а)все вышли на разных этажах; б) по крайней мере двое сошли на одном этаже.
Дано: k = 7, n = 4.
Решение.
а) Событие А – все пассажиры вышли на разных этажах.
Событие А1 – первый пассажир вышел на любом из шести, кроме первого, этаже.
Событие А2 – второй пассажир вышел на любом из оставшихся пяти этаже, т.е. кроме первого и этажа, на котором вышел первый пассажир.
Событие А3 – третий пассажир вышел на любом из оставшихся четырех этаже, т.е. кроме первого и этажей, на которых вышли первый и второй пассажиры.
Событие А4 – четвертый пассажир вышел на любом из оставшихся трех этаже, т.е. кроме первого и этажей, на которых вышли первый, второй и третий пассажиры.
Вероятность события А находим по теореме умножения, поскольку события А1, А2, А3, А4 являются зависимыми. Тогда:
![]()
где: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Отсюда:
![]() .
.
б) Событие В – по крайней мере двое сошли на одном этаже.
Событие В1 – первый пассажир вышел на любом из шести, кроме первого, этаже.
Событие В2 – второй пассажир вышел на любом из оставшихся пяти этаже, т.е. кроме первого и этажа, на котором вышел первый пассажир.
Событие В3 – третий пассажир вышел на любом из оставшихся четырех этаже, т.е. кроме первого и этажей, на которых вышли первый и второй пассажиры.
Событие В4 – четвертый пассажир вышел на любом из трех этаже, на которых вышли первый, второй и третий пассажиры.
Вероятность события В находим по теореме умножения, поскольку события В1, В2, В3, В4 являются зависимыми. Тогда:
![]()
где: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Отсюда:
![]() .
.
Ответ: а) 0,2778; б) 0,2778.
5. В двух партиях К1 и К2 % доброкачественных изделий на удачу выбирают по одному изделию из каждой партии Какова вероятность того, что среди двух изделий:
а) хотя бы одно бракованное;
б) два бракованных;
в) одно бракованное и одно доброкачественное.
Дано: К1 = 39%, К2 = 78%.
Решение.
Обозначим события:
Событие А – из первой партии наудачу вынули доброкачественное изделие;
Событие B - из второй партии наудачу вынули доброкачественное изделие
Вероятности этих событий соответственно равны: р1 = 0,39 и р2 = 0,78.
а) Пусть событий С – среди двух изделий хотя бы одно бракованное.
Рассмотрим противоположное событие ![]() - среди двух изделий нет бракованных, то есть эти два изделия доброкачественные. Вероятность события
- среди двух изделий нет бракованных, то есть эти два изделия доброкачественные. Вероятность события ![]() находим, используя теорему умножения:
находим, используя теорему умножения:
Р(![]() ) = р1 · р2 = 0,39 · 0,78 = 0,3042
) = р1 · р2 = 0,39 · 0,78 = 0,3042
Отсюда, вероятность искомого события Р(С) найдём по формуле:
Р(С) = 1 - Р(![]() ) = 1 – 0,3042 = 0,6958.
) = 1 – 0,3042 = 0,6958.
б) Пусть событий D – среди двух изделий два бракованных.
Вероятность события D находим, используя теорему умножения:
Р(D) = q1 · q2 = (1 - р1) · (1 - р2) = (1 - 0,39)·(1 - 0,78) = 0,1342.
в) Пусть событий Е - одно бракованное и одно доброкачественное. Здесь необходимо рассмотреть два события: Событие ![]() - из первой партии вынули доброкачественное изделия, а из второй – бракованное; Событие
- из первой партии вынули доброкачественное изделия, а из второй – бракованное; Событие ![]() - из первой партии вынули бракованное изделие, а из второй – доброкачественное.
- из первой партии вынули бракованное изделие, а из второй – доброкачественное.
Тогда:
Е = ![]() +
+![]()
или Р(Е) = Р(![]() ) + Р(
) + Р(![]() )
)
Вероятность события Е находим, используя теорему сложения и умножения:
Р(Е) = р1 · q2 + q1 · р2 = 0,39 · 0,22 + 0,61 · 0,78 = 0,5616
Ответ: а) 0,6958; б) 0,1342; в) 0,5616.
6. Вероятность того, что цель поражена при одном выстреле: первым стрелком равна P1 = 0,39, а вторым стрелком - P2 = 0,45. Первый стрелок сделал n1 = 3 выстрелов, а второй стрелок – n2 = 2 выстрелов. Определить Вероятность того, что цель не поражена.
Решение.
Пусть событие А - цель не поражена. Чтобы цель была не поражена, необходимо, чтобы первый стрелок, сделав 3 выстрела, ни разу не попал, и, чтобы второй стрелок, сделав 2 выстрела, тоже ни разу не попал.
Рассмотрим гипотезы:
Событие А1 – первый стрелок промахнулся 3 раза.
Событие А2 - второй стрелок промахнулся 2 раза.
Вероятность того, что первый стрелок промахнется при одном выстреле равна:
q1 = 1 - p1 = 1- 0,39 = 0,61,
а вероятность того, что второй стрелок промахнется при одном выстреле равна: q2 = 1 - p2 = 1- 0,45=0,55.
Тогда вероятность событий А1 и А2 находим по формуле Бернулли:
![]()
Тогда:
![]()
![]()
Тогда искомая вероятность события А, используя теорему умножения, равна:
Р(А) = Р(А1)×Р(А2) = 0,227 · 0,3025 = 0,0687.
Ответ: 0,0687.
7. Из ![]() ламп ni принадлежат i-й партии (i = 1, 2, 3) бракованные лампы в первой партии составляют 6%, во второй – 5%, а в третьей – 4%. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа - бракованная.
ламп ni принадлежат i-й партии (i = 1, 2, 3) бракованные лампы в первой партии составляют 6%, во второй – 5%, а в третьей – 4%. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа - бракованная.
Дано: n1 = 620, n2 = 190.
Решение.
Испытание состоит в том, что наудачу выбирают одну лампу.
Пусть событие А - выбранная лампа – бракованная. Рассмотрим гипотезы:
Событие Н1 – выбранная лампа принадлежит 1-й партии,
Событие Н2 – выбранная лампа принадлежит 2-й партии,
Событие Н3 – выбранная лампа принадлежит 3-й партии.
Вероятность события А находим по формуле полной вероятности:
![]()
Определяем вероятности гипотез Н1, Н2, Н3 с помощью классического определения вероятности:
![]() ,
,
Для события Н1 имеем: m1 = 620 (количество ламп в первой партии), n =1000 (общее количество ламп); тогда вероятность события Н1 равна:
![]()
Аналогично находим вероятности гипотез Н2 и Н3.
Для события Н2 имеем: m2 = 190, n =1000.
![]()
Для события Н3 имеем: m3 = 1000 - m1 – m2 = 1000 – 620 –190 = 190, n =1000.
![]()
Контроль:
![]()
Находим условные вероятности события А при условии, что события Н1, Н2, Н3 соответственно наступили, то есть вероятности ![]() ,
,![]() и
и ![]() , по формуле:
, по формуле:
![]()
где: ki – число процентов бракованных ламп в i-й партии. Тогда
![]()
![]()
![]()
Подставляя найденные вероятности в формулу полной вероятности, находим вероятность события А:
![]() =
=
= 0,62 · 0,06 + 0,19 · 0,05 + 0,19 · 0,04 = 0,0543.
Ответ: Р(А) = 0,0543.
8. В первой урне N1 белых и M1 чёрных шаров, во второй N2 белых и M2 чёрных шаров. Из первой урны во вторую переложили К шаров, затем из второй урны извлечен один шар. Определить вероятность того, что выбранный из второй урны шар – белый.
Дано: N1 = 20, M1 = 1, N2 = 40, M2 = 7, К = 15.
Решение.
Испытание состоит в том, что наудачу выбирают из второй урны шар после перекладывания из первой урны во вторую 15 шаров.
Пусть событие А - выбранный шар – белый.
Рассмотрим гипотезы:
Событие Н1 – из первой урны во вторую переложили 15 шаров, среди которых 15 белых и ни одного чёрного;
Событие Н2 – из первой урны во вторую переложили 15 шаров, среди которых 14 белых и 1 чёрный; Так как события Н1, Н2 образуют полную группу событий, и событие А может произойти с одним из этих событий, вероятность события А находим по формуле полной вероятности:

Определяем вероятности гипотез Н1, Н2 с помощью классического определения вероятности:
![]() ,
,
где: mi – число исходов, благоприятствующих появлению события Hi, n – общее число равновозможных исходов испытания.
В первой урне находится (N1 + M1) = 20+1 =21 шар, тогда общее число равновозможных исходов испытания равняется числу способов, которыми можно вынуть 15 шаров из 21, то есть
n = ![]()
Находим вероятность гипотезы Н1. 15 белых шаров из 20 можно выбрать ![]() способами, а 0 чёрных из 1 -
способами, а 0 чёрных из 1 - ![]() способами, тогда число исходов, благоприятствующих появлению события Н1, используя теорему умножения, будет равно:
способами, тогда число исходов, благоприятствующих появлению события Н1, используя теорему умножения, будет равно:
m = ![]() ×
×![]() =
=![]()
Отсюда, вероятность события Н1 равна:
![]()
Аналогично находим вероятности гипотез Н2.
Для события Н2 имеем:
m2=![]() ×
×![]() =
=![]()
Отсюда, вероятность события Н2 равна:
![]()
Контроль:
![]()
Находим условные вероятности события А при условии, что события Н1, Н2 соответственно наступили, то есть вероятности ![]() ,
, ![]() с помощью классического определения вероятности:
с помощью классического определения вероятности:
![]() ,
,
где: mi – число исходов, благоприятствующих появлению события А при условии, что событие Нi соответственно наступило; n – общее число равновозможных исходов испытания.
При наступлении события Н1 во второй урне станет (40+15)=55 белых и 7 чёрных шаров, всего в урне 62 шара, тогда для события A | Н1 имеем:
m1 = 55, a n = 62, отсюда
![]()
При наступлении события Н2 во второй урне станет (40+14)=54 белых и (7+1)=8 чёрных шаров, всего в урне 62 шаров, тогда для события A | Н2 имеем:
m2 = 54, a n = 62, отсюда
![]()
Таким образом, подставляя найденные вероятности в формулу полной вероятности, находим вероятность события А:
![]()
=0,2857×0,8871 + 0,7143×0,871 = 0,8756
Ответ: Р(А) = 0,8756.
9. В альбоме k чистых и l гашеных марок. Из них наудачу извлекаются m марок (среди которых могут быть и чистые, и гашенные), подвергаются спецгашению и возвращаются в альбом. После этого вновь наудачу извлекаются n марок. Определить вероятность того, что все n марки - чистые.
Дано: k = 7, l = 5, m = 2, n = 2.
Решение.
Испытание состоит в том, что наудачу выбирают из альбома после гашения 2 марки.
Пусть событие А - все 2 марки - чистые.
Рассмотрим гипотезы:
Событие Н1 – из альбома извлекли и подвергли спецгашению 2 чистые и ни одной гашеной марки;
Событие Н2 – из альбома извлекли и подвергли спецгашению 1 чистую и 1 гашеную марки;
Событие Н3 – из альбома извлекли и подвергли спецгашению ни одной чистой и 2 гашеные марки.
Так как события Н1, Н2, Н3 образуют полную группу событий, и событие А может произойти с одним из этих событий, вероятность события А находим по формуле полной вероятности:
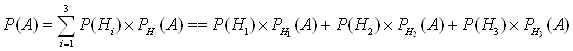
Определяем вероятности гипотез Н1, Н2, Н3 с помощью классического определения вероятности:
![]() ,
,
где: mi – число исходов, благоприятствующих появлению события Hi, n – общее число равновозможных исходов испытания.
Из альбома можно вынуть 2 марки из (k + l) = (7 + 5) = 12 марок - ![]() способами, тогда общее число равновозможных исходов испытания равно:
способами, тогда общее число равновозможных исходов испытания равно:
n = ![]()
Находим вероятность гипотезы Н1 2 чистые марки из 7 можно выбрать ![]() способами, а 0 гашенных из 5 -
способами, а 0 гашенных из 5 - ![]() способами, тогда число исходов, благоприятствующих появлению события Н1, используя теорему умножения, будет равно:
способами, тогда число исходов, благоприятствующих появлению события Н1, используя теорему умножения, будет равно:
m = ![]() ×
×![]() =
=![]()
Отсюда, вероятность события Н1 равна:
![]()
Аналогично находим вероятности гипотез Н2 и Н3:
Для события Н2 имеем:
m2=![]() ×
×![]() =
=![]()
Отсюда, вероятность события Н2 равна:
![]()
Для события Н3 имеем:
m3=![]() ×
×![]() =
=![]()
Отсюда, вероятность события Н3 равна:
![]()
Контроль:
![]()
Находим условные вероятности события А при условии, что события Н1, Н2, Н3 соответственно наступили, то есть вероятности ![]() ,
,![]() и
и ![]() с помощью классического определения вероятности:
с помощью классического определения вероятности:
![]() ,
,
где: mi – число исходов, благоприятствующих появлению события А при условии, что событие Нi соответственно наступило; n – общее число равновозможных исходов испытания.
При наступлении события Н1 в альбоме станет (7-2)=5 чистых и (5+2)=7 гашеных марок, всего в альбоме 12 марок, тогда для события A | Н1 имеем: m1 = ![]() - число способов, которыми можно выбрать 2 чистых марки из 5. n =
- число способов, которыми можно выбрать 2 чистых марки из 5. n = ![]() - число способов, которыми можно выбрать 2 марки из 12.
- число способов, которыми можно выбрать 2 марки из 12.
Отсюда
![]()
При наступлении события Н2 в альбоме станет (7-1)=6 чистых и (5+1)=6 гашеных марок, всего в альбоме 12 марок, тогда для события A | Н2 имеем: m2 = ![]() - число способов, которыми можно выбрать 2 чистых марки из 6. n =
- число способов, которыми можно выбрать 2 чистых марки из 6. n = ![]() - число способов, которыми можно выбрать 2 марки из 12.
- число способов, которыми можно выбрать 2 марки из 12.
Отсюда
![]()
При наступлении события Н3 в альбоме станет (7-0)=7 чистых и (5+0)=5 гашеных марок, всего в альбоме 12 марок, тогда для события A | Н3 имеем: m3 = ![]() - число способов, которыми можно выбрать 2 чистых марки из 7. n =
- число способов, которыми можно выбрать 2 чистых марки из 7. n = ![]() - число способов, которыми можно выбрать 2 марки из 12.
- число способов, которыми можно выбрать 2 марки из 12.
Отсюда
![]()
Таким образом, подставляя найденные вероятности в формулу полной вероятности, находим вероятность события А:
![]()
= 0,3182 · 0,1515 + 0,5303 · 0,2273 + 0,1515 · 0,3182 = 0,217.
Ответ: Р(А) = 0,217.
10. В магазин поступают однотипные изделия с 3-х заводов, причем i–й завод поставляет mi% изделий. Среди изделий i–го завода ni % - первосортных. Куплено одно изделие. Оно оказалось первосортным. Найти вероятность того, что купленное изделие выпущено j-м заводом?
Дано: m1 = 60%, m2 = 10%, m3 = 30%, n1 = 80%, n2 = 90%, n3 = 80%, j = 3.
Решение.
Испытание состоит в том, что наудачу покупают одно изделие.
Рассмотрим событие А – изделие оказалось первосортным.
Рассмотрим гипотезы:
Событие H1 – наудачу купленное изделие изготовлено на 1-ом заводе.
Событие H2 – наудачу купленное изделие изготовлено на 2-ом заводе.
Событие H3 – наудачу купленное изделие изготовлено на 3-ем заводе.
По условию задачи необходимо найти вероятность события Н3|А, то есть события состоящего в том, что наудачу купленное изделие изготовлено на 3-ем заводе, если известно, что она первосортное.
Так как события H1, H2 и H3 образуют полную группу событий, и событие А может наступить с одним из этих событий, то для нахождения вероятности события ![]() воспользуемся формулой Байеса:
воспользуемся формулой Байеса:
![]() ,
,
где полная вероятность события А, которая может быть определена по формуле полной вероятности:
![]()
Определяем вероятности гипотез Н1, Н2, Н3 с помощью классического определения вероятности:
![]() ,
,
где: mi – число исходов, благоприятствующих появлению события Hi, n – общее число равновозможных исходов испытания.
Для события Н1 имеем: m1 = 60% (количество изделий, изготовленных на 1-ом заводе), n = 100% (общее количество изделий); тогда вероятность события Н1 равна:
![]()
Аналогично находим вероятности гипотез Н2 и Н3.
Для события Н2 имеем: m2 = 10% (количество изделий, изготовленных на 2-ом заводе), n = 100% (общее количество изделий); тогда вероятность события Н2 равна:
![]()
Для события Н3 имеем: m3 = 30% (количество изделий, изготовленных на 3-ем заводе), n = 100% (общее количество изделий); тогда вероятность события Н3 равна:
![]()
Контроль:
![]()
Находим условные вероятности события А при условии, что события Н1, Н2, Н3 соответственно наступили, то есть вероятности ![]() ,
,![]() и
и ![]() , по формуле:
, по формуле:
![]()
где: ki –число стандартных изделий, изготовленных на i – заводе, mi – общее число изделий, изготовленных на i – заводе. Тогда
![]()
![]()
![]()
Таким образом, подставляя найденные вероятности в формулу полной вероятности, находим вероятность события А:
![]() =
=
= 0,6 × 0,8 + 0,1 × 0,9 + 0,3 × 0,8 = 0,81.
Отсюда, по формуле Байеса получим: ![]() .
.
Ответ: ![]() .
.
Похожие работы
... vij матрицы весов. Используя венгерский алгоритм, найти совершенное паросочетание минимального (максимального веса). Выполнить рисунок. Матрица весов двудольного графа K55 : y1 y2 y3 y4 y5 x1 2 0 0 0 0 x2 0 7 9 8 6 x3 0 1 3 2 2 x4 0 8 7 6 4 x5 0 7 6 8 3 Первый этап - получение нулей не нужен, т. к. нули уже есть во всех строк и столбцах. Второй этап - ...
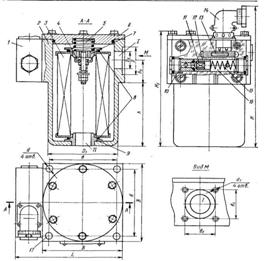
... в каждом конкретном случае исходя из габаритов проектируемого технического оборудования, места расположения насосной станции и рабочих органов машины, способов монтажа гидрооборудования и других условий. Для технологического оборудования малых и средних типоразмеров можно принять длины участков в следующих пределах: всасывающий трубопровод- до 1 метра, напорный и сливной до 5 метров. Для ...
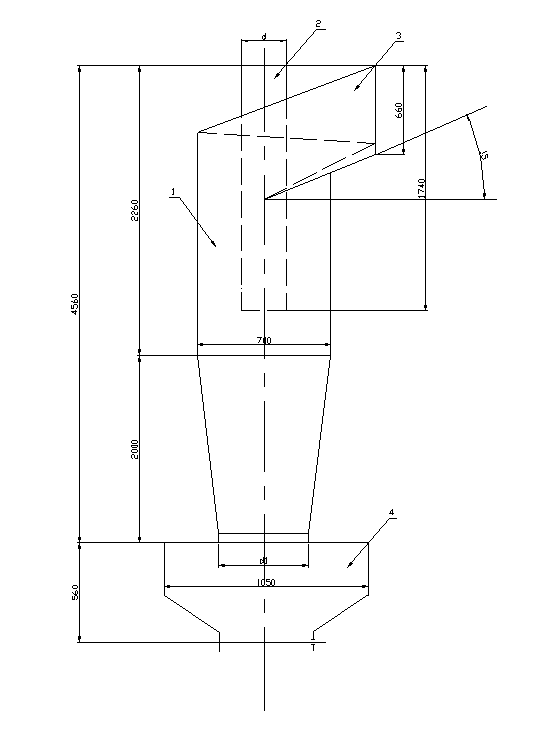
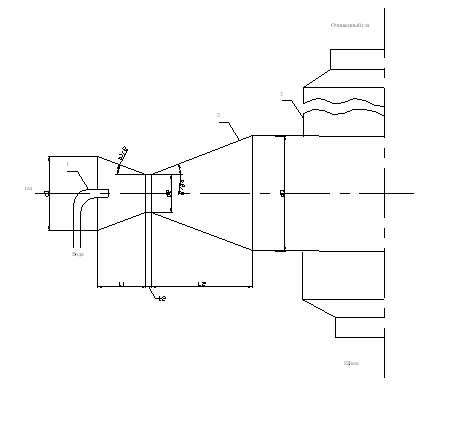
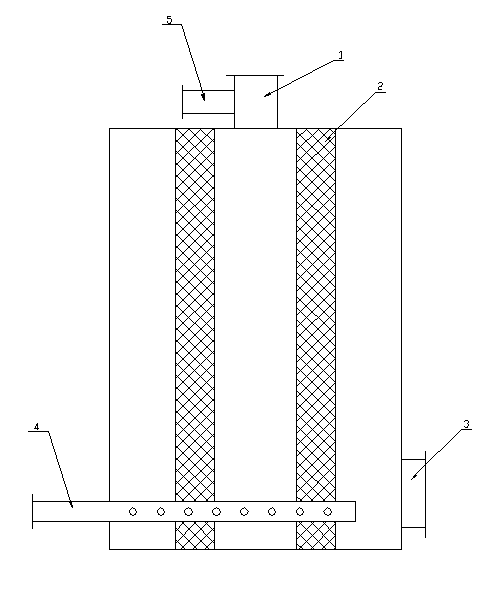
... м3/с Vг = Мг/rг = 0,9/0,9 = 1 м3/с Кт = 10662855 + 300×103(8,65×10-4/1) = 10663114 Па Определяем эффективность скруббера Вентури Эффективность скруббера Вентури, полученная в результате расчетов (величина ), удовлетворяет заданному условию, т.е. обеспечивает очистку газов от пыли с эффективностью не менее 0.9. Рис. 2.1 Скруббер Вентури 1 – форсунки 2 – сопло 3 – ...
... нефтепровода, м 25 ρ - средняя плотность, т/м3 0,870 P1 - давление насосной станции, кгс/см2 46 P2 - давление в конце участка, кгс/см2 1,5 δ - толщина стенки, мм 14 Таблица 2 - Данные для прочностного расчета Параметры Вариант 3 Dн - диаметр трубопровода наружный, мм 1220 Марка стали 12 Г2СБ t0 - температура при сварке замыкающего стыка, 0с ...
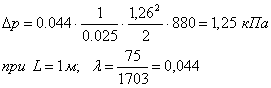
0 комментариев