Навигация
Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции
6. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.
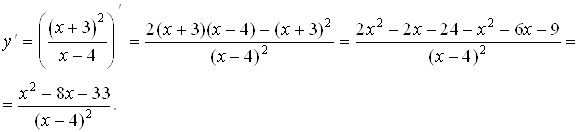
Из ![]() получаем
получаем ![]() , откуда
, откуда ![]() ,
, ![]() .
.
+ _ +
______________________________________ x
-3 11
Так как на интервалах ![]() и
и ![]() производная положительна, т.е.
производная положительна, т.е. ![]() , то график функции на указанных интервалах возрастает. Так как на интервале
, то график функции на указанных интервалах возрастает. Так как на интервале ![]() производная отрицательна, т.е.
производная отрицательна, т.е. ![]() , то на указанном интервале график функции убывает.
, то на указанном интервале график функции убывает.
Так как при переходе через точки ![]() ,
, ![]() производная функции меняет знаки и эти точки входят в область определения функции, то
производная функции меняет знаки и эти точки входят в область определения функции, то ![]() ,
, ![]() - точки локального экстремума. Причем
- точки локального экстремума. Причем ![]() точка локального минимума:
точка локального минимума: ![]() (так как при переходе через нее производная меняет знак с "+" на "-");
(так как при переходе через нее производная меняет знак с "+" на "-");
![]() - точка локального максимума:
- точка локального максимума: ![]() (так как при переходе через нее производная меняет знак с "-" на "+").
(так как при переходе через нее производная меняет знак с "-" на "+").
7. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем вторую производную функции.

Очевидно, что в интервале ![]() вторая производная меньше нуля, т.е.
вторая производная меньше нуля, т.е. ![]() , и в этом интервале график функции является выпуклым вверх. В интервале
, и в этом интервале график функции является выпуклым вверх. В интервале ![]() вторая производная больше нуля, т.е.
вторая производная больше нуля, т.е. ![]() , и в этом интервале график функции является выпуклым вниз (вогнутым).
, и в этом интервале график функции является выпуклым вниз (вогнутым).
Несмотря на то, что при переходе через точку ![]() вторая производная меняет знак, она не является точкой перегиба, так как
вторая производная меняет знак, она не является точкой перегиба, так как ![]() не входит в область определения функции, т.е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.
не входит в область определения функции, т.е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.
Из ![]() получаем
получаем ![]() , откуда
, откуда ![]() ,
, ![]() .
.
+ _ +
______________________________________ x
-3 11
Так как на интервалах ![]() и
и ![]() производная положительна, т.е.
производная положительна, т.е. ![]() , то график функции на указанных интервалах возрастает. Так как на интервале
, то график функции на указанных интервалах возрастает. Так как на интервале ![]() производная отрицательна, т.е.
производная отрицательна, т.е. ![]() , то на указанном интервале график функции убывает.
, то на указанном интервале график функции убывает.
Так как при переходе через точки ![]() ,
, ![]() производная функции меняет знаки и эти точки входят в область определения функции, то
производная функции меняет знаки и эти точки входят в область определения функции, то ![]() ,
, ![]() - точки локального экстремума. Причем
- точки локального экстремума. Причем ![]() точка локального минимума:
точка локального минимума: ![]() (так как при переходе через нее производная меняет знак с "+" на "-");
(так как при переходе через нее производная меняет знак с "+" на "-");
![]() - точка локального максимума:
- точка локального максимума: ![]() (так как при переходе через нее производная меняет знак с "-" на "+").
(так как при переходе через нее производная меняет знак с "-" на "+").
Часто возникает задача, обратная той, которая решалась в дифференциальном исчислении, а именно: дана функция ![]() , найти функцию
, найти функцию ![]() , такую, что
, такую, что ![]() .
.
Функция ![]() называется первообразной для данной функции
называется первообразной для данной функции ![]() на некотором промежутке Х, если для любого
на некотором промежутке Х, если для любого ![]() выполняется равенство
выполняется равенство
![]() .
.
Например, пусть ![]() , тогда за первообразную можно взять
, тогда за первообразную можно взять ![]() , поскольку
, поскольку ![]() .
.
В основе интегрального исчисления лежит теорема об общем виде первообразной: если ![]() – первообразная для функции
– первообразная для функции ![]() на промежутке Х, то все первообразные для функции
на промежутке Х, то все первообразные для функции ![]() имеют вид
имеют вид ![]() , где С – произвольная постоянная.
, где С – произвольная постоянная.
Выражение вида ![]() описывает все первообразные для функции
описывает все первообразные для функции ![]() . Действительно, для любой постоянной С
. Действительно, для любой постоянной С
![]() .
.
Пусть наряду с данной первообразной ![]() функция
функция ![]() – также первообразная для
– также первообразная для ![]() . Тогда должны выполняться равенства
. Тогда должны выполняться равенства
![]() ,
,
откуда ![]() . Следовательно, разность этих первообразных будет тождественно равна константе
. Следовательно, разность этих первообразных будет тождественно равна константе ![]() или
или ![]() .
.
Действие нахождения первообразной называется интегрированием функции.
Доказанная теорема позволяет ввести основное понятие интегрального исчисления: если ![]() – первообразная для
– первообразная для ![]() , то совокупность функций
, то совокупность функций ![]() , где С – произвольная постоянная, называется неопределенным интегралом от функции
, где С – произвольная постоянная, называется неопределенным интегралом от функции ![]() , который обозначается следующим образом
, который обозначается следующим образом
![]() .
.
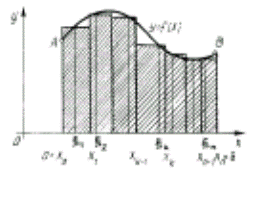
Геометрически неопределенный интеграл представляет собой семейство плоских кривых ![]() , называемых интегральными.
, называемых интегральными.
Для того, чтобы проверить, правильно ли выполнено интегрирование, надо взять производную от результата и убедиться, что получена подынтегральная функция ![]() . Как всякая обратная операция, интегрирование – более сложное действие, чем дифференцирование.
. Как всякая обратная операция, интегрирование – более сложное действие, чем дифференцирование.
Приведем основные свойства неопределенного интеграла:
1. производная неопределенного интеграла равна подынтегральной функции
![]() ;
;
2. неопределенный интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых функций
![]() ;
;
3. постоянный множитель можно выносить за знак неопределенного интеграла
![]() .
.
Значения интегралов от основных элементарных функций получаются из формул дифференцирования этих функций. Приведем таблицу основных интегралов:
| 1) | 7) |
| 2) | 8) |
| 3) | 9) |
| 4) | 10) |
| 5) | 11) |
| 6) | 12) |
Интегралы, содержащиеся в этой таблице, называются табличными.
Пример. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием
![]()
Решение: Для нахождения неопределенных интегралов можно воспользоваться как методом замены переменной, так и методом внесения под знак дифференциала. Покажем оба метода.
1. Воспользуемся методом замены переменной. Введем новую переменную t по формуле ![]() . Тогда
. Тогда ![]() или
или ![]() . Тогда
. Тогда

После замены переменной воспользовались свойством неопределенного интеграла: постоянный множитель ![]() можно выносить за знак неопределенного интеграла, и так как
можно выносить за знак неопределенного интеграла, и так как ![]() , то пришли к табличному интегралу
, то пришли к табличному интегралу ![]() , где
, где ![]() и
и ![]() .
.
2. Решим этот пример методом внесения под знак дифференциала. Замечая, что ![]() и то, что подынтегральное выражение можно представить в виде
и то, что подынтегральное выражение можно представить в виде
![]() ,
,
внесем под знак дифференциала ![]() . Для этого выпишем дифференциал этой функции
. Для этого выпишем дифференциал этой функции ![]() . Тогда
. Тогда
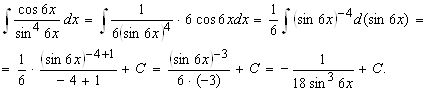
После внесения под знак дифференциала функции ![]() пришли к табличному интегралу
пришли к табличному интегралу ![]() , где
, где ![]() и
и ![]() .
.
Похожие работы
... дробей m и n; 2) если Z, то используется подстановка: a+bxn=ts, где s – знаменатель дроби 3) если Z, то применяется подстановка: ax-n+b=ts, где s – знаменатель дроби 9. Понятие определенного интеграла, его геометрический смысл. Определение. Если существует конечный передел интегральной суммы (8) - (8) при λ→0, не зависящий от способа разбиения &# ...
... элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций. Из определения 2 следует: 1.Производная от неопределенного интеграла равна подынтегральной функции, т.е.если F′ (x)= f(x), то и (∫ f(x)dx)′= (F(x)+C)′=f(x). (4) Последнее равенство нужно понимать в том смысле, что ...
... по алгебре и началам анализа, при подготовке к государственной итоговой аттестации, внешнему независимому оцениванию. Достаточно большое число задач раскрывают потенциальные возможности анализа бесконечно малых величин. 1. Производная и ее применение для решения прикладных задач 1.1 Исторические сведения Ряд задач дифференциального исчисления был решен еще в древности. Они встречались у ...
... в потенциальную, и обратно. Но на рубеже 17-18 веков никто не догадался, что именно законы сохранения составляют следующий по глубине слой природных закономерностей. Их понимание потребовало новой революции в математике: изучения природных симметрий с помощью теории групп. Ее создание и применение заняло весь 19 век и большую часть 20 века. Предугадать такое развитие математики Ньютон не мог - ...
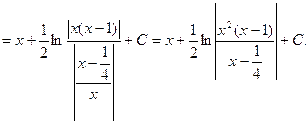

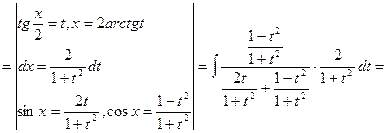
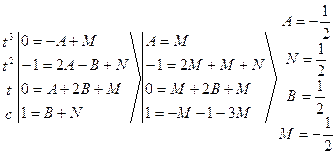


0 комментариев