Навигация
5. Теорема Гурвица
Рассмотрим n-мерное Евклидово пространство ![]() . Если
. Если ![]() , то его длиной называют число
, то его длиной называют число ![]() . Естественно поставить
. Естественно поставить
Вопрос 1. Для каких n существует билинейное отображение ![]() такое, что
такое, что ![]() для любых
для любых ![]() ?
?
Заметим, что, если выполнено это условие ![]() , то
, то ![]() -алгебра без делителей нуля (т.к.
-алгебра без делителей нуля (т.к. ![]() и либо а=0, либо b=0). Более того, если
и либо а=0, либо b=0). Более того, если ![]() , то для любого и разрешимо уравнение
, то для любого и разрешимо уравнение ![]() и
и ![]() . Т.к. отображения
. Т.к. отображения ![]() и
и ![]() имеют нулевые ядра и следовательно являются сюръективными (т.е.
имеют нулевые ядра и следовательно являются сюръективными (т.е.![]() является телом, вообще говоря неассоциативным и некоммутативным). Если
является телом, вообще говоря неассоциативным и некоммутативным). Если ![]() ортонормированный базис
ортонормированный базис ![]() , то
, то ![]() и если
и если ![]() , то
, то ![]() , где
, где ![]() и условие
и условие ![]() эквивалентно следующему вопросу.
эквивалентно следующему вопросу.
Вопрос 2: Для каких n существует тождество ![]() , где
, где ![]() -любые действительные числа,
-любые действительные числа, ![]() и матрицы
и матрицы ![]() являются постоянными, т.е. не зависят от
являются постоянными, т.е. не зависят от ![]() ?
?
В 1989 году Гурвиц доказал, что представлять произведение целых чисел в виде сумм квадратов целых чисел можно только для множителей, состоящих из сумм двух, четырех и восьми квадратов.
Теорема 4: Вопросы 1-2 имеют решение только при n=1,2,4,8.
Доказательство: Будем считать, что ![]() . Положим
. Положим ![]() ,
,![]() . Тогда равенство
. Тогда равенство ![]() =
=![]() , где
, где ![]() переписывается в виде
переписывается в виде
![]() =
=![]() .
.
Фиксируем ![]() и рассмотрим левую и правую части многочлена от
и рассмотрим левую и правую части многочлена от ![]() .Тогда
.Тогда
![]() ,
,
![]()
![]() ,
,![]()
Если ![]() , то предыдущие равенства равносильны
, то предыдущие равенства равносильны ![]() . Перепишем
. Перепишем ![]() , где
, где ![]() (т.е.
(т.е. ![]() не зависит от
не зависит от ![]() ). Тогда из равенства
). Тогда из равенства ![]() следует эквивалентное равенство
следует эквивалентное равенство ![]() , сравнивая коэффициенты при
, сравнивая коэффициенты при ![]() , последнее влечет за собой
, последнее влечет за собой ![]() , i=1,2,..,n и ,следовательно,
, i=1,2,..,n и ,следовательно, ![]() . Положим
. Положим ![]() . Тогда предыдущее равенство можно переписать в виде:
. Тогда предыдущее равенство можно переписать в виде:
![]() ,
, ![]()
*![]() .
.
Сравнивая коэффициенты при ![]() , получим, что
, получим, что ![]() ,
,![]()
![]() ,
,![]() . Получим
. Получим ![]() ,
, ![]()
![]() или
или ![]() ,
, ![]()
![]() ,
, ![]() . Покажем, что существование таких матриц
. Покажем, что существование таких матриц ![]() влечет за собой, что n=2,4,8.
влечет за собой, что n=2,4,8.
![]() -кососимметричная и невырожденная. Значит n-четное число. В частности
-кососимметричная и невырожденная. Значит n-четное число. В частности ![]()
Породим этими матрицами подалгебру
![]()
Матрица вида ![]() , где
, где ![]() является системой K . Их число равно
является системой K . Их число равно ![]() . Покажем, что, по меньшей мере,
. Покажем, что, по меньшей мере, ![]() из них линейно независимы. Для этого сначала заметим, что
из них линейно независимы. Для этого сначала заметим, что ![]() ,
, ![]() удовлетворяет
удовлетворяет
![]() =
=
=![]()
В частности М - симметричная тогда и только тогда, когда ![]() , либо
, либо ![]() . Если существует соотношение
. Если существует соотношение ![]() , где
, где ![]() -слева от
-слева от ![]() , то можно считать, что все
, то можно считать, что все ![]() и все собственные подмножества
и все собственные подмножества ![]() являются линейно независимыми. Тогда, умножая на
являются линейно независимыми. Тогда, умножая на ![]() , получим соотношение вида:
, получим соотношение вида: ![]() . При этом все
. При этом все ![]() являются симметричными (ввиду линейной независимости
являются симметричными (ввиду линейной независимости ![]() ).
).
Пусть ![]() вовлекает наименьшее число факторов r . Тогда
вовлекает наименьшее число факторов r . Тогда
![]() .
.
Если ![]() и
и ![]() , то выберем
, то выберем ![]() и умножим левую и правые части на
и умножим левую и правые части на ![]() . Получим, что
. Получим, что ![]() . Т.к.
. Т.к. ![]() -кососимметричная, а
-кососимметричная, а ![]() -симметричная, то получили противоречие.
-симметричная, то получили противоречие.
Если ![]() , то умножим обе части на
, то умножим обе части на ![]() . Получим, что
. Получим, что ![]() , где
, где ![]() ( их количество 4e-1) – симметричная матрица, а слева кососимметричная матрица. Противоречие. Следовательно,
( их количество 4e-1) – симметричная матрица, а слева кососимметричная матрица. Противоречие. Следовательно, ![]() и
и ![]() , и как показывают рассуждения выше, либо
, и как показывают рассуждения выше, либо ![]() , либо
, либо ![]() . Если
. Если ![]() , то, умножая на
, то, умножая на ![]() , получим, что
, получим, что ![]() (их число n-2=4e-1) – симметричная. Противоречие. следовательно
(их число n-2=4e-1) – симметричная. Противоречие. следовательно ![]() . В частности, если
. В частности, если ![]() и
и ![]() , то получаем противоречие, т.е.
, то получаем противоречие, т.е. ![]() . Пусть
. Пусть ![]() . Докажем, что
. Докажем, что ![]() - линейно независимы. Их число равно
- линейно независимы. Их число равно ![]() . Действительно, если между ними есть линейно зависимые, то получим, что
. Действительно, если между ними есть линейно зависимые, то получим, что ![]() , где длина
, где длина
![]()
![]() ,
, ![]()
Длина
![]()
Т.е. мы не получили ![]() . Противоречие.
. Противоречие.
Итак, ![]() и
и ![]() . Это возможно при
. Это возможно при ![]() . Если n<10, то при n=2,4,8 теорема верна. Далее n-четное число. Осталось понять, что при n=6 кососимметричные матрицы из
. Если n<10, то при n=2,4,8 теорема верна. Далее n-четное число. Осталось понять, что при n=6 кососимметричные матрицы из ![]() линейно независимы.
линейно независимы.
![]() в
в ![]() .
.
С другой стороны, среди ![]() , где
, где ![]() (их число равно 32) количество кососимметричных равно
(их число равно 32) количество кососимметричных равно ![]() . Т.к.
. Т.к. ![]() , то все эти матрицы
, то все эти матрицы ![]() линейно независимы. В частности и эти линейно независимы
линейно независимы. В частности и эти линейно независимы ![]() . С другой стороны их число меньше 15. Противоречие. (Можно сослаться что
. С другой стороны их число меньше 15. Противоречие. (Можно сослаться что ![]() , 6-не подходит).
, 6-не подходит).
Таким образом, теорема Гурвица доказана. [1]
Пример 2:
![]()
![]()
![]()
Можно ответить на вопрос Гурвица в случае s=n. Это сделал сам Гурвиц в конце жизни, через 20 лет после того, как поставил свой вопрос. Ответ, оказывается, связан с представлениями алгебр Клиффорда. Ответ звучит так: формула типа (r, n, n) существует тогда и только тогда, когда число r не превосходит числа p, зависящего от n следующим образом. Пусть ![]() -наибольшая степень двойки, на которую делится число n. Разделим
-наибольшая степень двойки, на которую делится число n. Разделим ![]() на 4 с остатком. Обозначим через a неполное частное, а через b остаток. Тогда
на 4 с остатком. Обозначим через a неполное частное, а через b остаток. Тогда ![]() =4a+b,
=4a+b, ![]() . Число p равно
. Число p равно ![]() [5]
[5]
Похожие работы
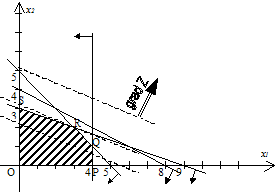
... стратегии игрока В. Задача имеет решение игры, если её матрицы не содержит седловой точки (). Расчет выигрышей производится по целевой функции: Система ограничения: 2.3.Описания метода Гурвица 2.3.1. Выбираем по строкам наименьший выигрыш и заполняем колонку а. 2.3.2. Выбираем по строкам наибольший выигрыши и заполняем колонку 2.3.3. Производим расчёт выигрыша по формуле: ; ...
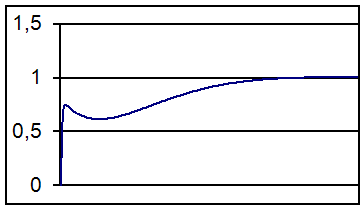
... процесс является колебательным и имеет А1 и А3 (первая и третья амплитуды переходного процесса), то можно найти и степень затухания. 6. Функциональная схема Системы Автоматического Управления в общем виде выглядит следующим образом: 7. Вывод Математическая модель объекта регулирования системы, полученная в работе, является достаточно адекватной исходным данным. Об ...
... , чем обычно. Общий заработок в 1000 $ они должны поделить следующим образом: певцу 350 $, пианисту 435 $, ударнику 175 $. Глава . Принятие решений в условиях частичной неопределенности. Элементы теории статистических решений. Предметом рассмотрения данного раздела служат статистические модели приянятия решений, трактуемые как статистические игры или игры с природой при использовании ...
... какая-либо из имеющихся. ж) Придумайте взвешивающую формулу (ее придется объяснить при защите курсовой работы!) и найдите по ней худшую и лучшую операции. 18. Произвести математико-статистический анализ за T лет Xt, Kt, Lt (t = 1, …, T) о выпуске продукции (в стоимостном виде), ОПФ и числе занятых исследуемого производственного экономического объекта: а) найти прогноз выпуска, фондов ...

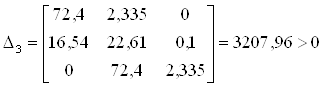
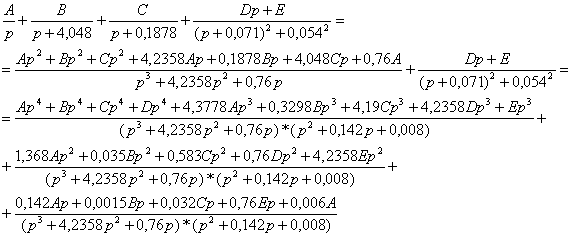
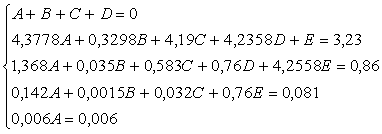
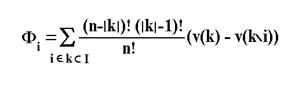
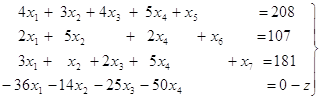

0 комментариев