Навигация
5. Ряды Фурье-Бесселя
Рассмотрим на каком-либо интервале 
(конечном или бесконечном) два дифференциальных уравнения
, 
, (20)
где 
и 
– непрерывные функции на . Пусть 
и 
– ненулевые решения этих уравнений. Умножение на и на и последующее вычитание дают
.
Пусть 
и 
принадлежат и 
, тогда после интегрирования в пределах от до получим
. (21)
Если и – соседние нули решения 
, то между и сохраняет постоянный знак, пусть, например, 
на (, ) (в противном случае следует заменить на 
), тогда 
, 
(равенство нулю исключено, так как – ненулевое решение дифференциального уравнения второго порядка). Если на 
, то должна, по крайней мере, раз обращаться в нуль между и , так как иначе сохранит постоянный знак на (,). Пусть, например, 
на (,) (в противном случае заменяем на 
), и тогда из (21) получим противоречие, ибо левая часть ≤0, а правая >0. Таким образом доказана теорема сравнения Штурма: если P(x)<Q(x) на рассматриваемом интервале I и если y и z – ненулевые решения уравнений (20), то между каждыми двумя соседними нулями y(x) находится по крайней мере один нуль z(x).
Из теоремы сравнения Штурма вытекают нижеследующие следствия. Если 
на , то каждое ненулевое решение уравнения 
может иметь на не более одного нуля (это легко видеть, если положить 
и взять 
). Если 
на (где 
), то для всяких двух соседних нулей и (
) каждого ненулевого решения уравнения имеем 
(это легко видеть, если положить 
, взять 
и заметить, что нулями будут только числа вида 
, 
целое). Если 
на (где 
), то для всяких двух соседних нулей каждого ненулевого решения уравнения 
имеем 
(это легко видеть, если положить 
и взять 
). Из сказанного следует, что если 
на , то для всяких двух соседних нулей и () каждого ненулевого решения уравнения имеем 
.
Изложенное показывает, что если 
непрерывна на 
и превышает некоторое положительное число вблизи +∞, то каждое ненулевое решение уравнения имеет на бесконечно много нулей. Если еще вблизи 
не обращается в нуль, то эти нули образуют бесконечную возрастающую последовательность 
, имеющую пределом +∞, а если, кроме того, 
, где 
, то 
.
Рассмотрим уравнение Бесселя
на интервале 
. Подстановка 
приводит к уравнению
.
Очевидно, и имеют одни и те же нули. Так как 
, где 
– целая функция, то 
не имеет нулей на 
при достаточно малом 
, и так как 
при 
, то при каждом 
нули на образуют бесконечную возрастающую последовательность
причем 
.
Если 
, то 
удовлетворит уравнению
на интервале (0, +∞). Подстановка приводит к уравнению
и, следовательно, 
удовлетворяет этому уравнению. Таким образом, при любых положительных и имеем
, где 
,
, где 
,
откуда
,
следовательно,
, где 
. (22)
Пусть теперь 
. Разложение 
по степеням 
начинается с члена, содержащего 
, разложение 
по степеням начинается с члена, содержащего 
, так как коэффициент при 
равен нулю, что легко видеть, исходя из формулы (5). Следовательно, из (22) при 
получим
,
то есть
, (23)
откуда видно, что если и являются разными нулями функции , то
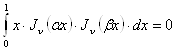. (23`)
Этим доказано, что при система функций
на интервале 
является ортогональной относительно веса 
.
Переходя к пределу при 
в соотношении
и используя правило Лопиталя, получим при всяком 
, (24)
следовательно, если является нулем функции , то
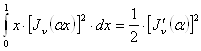. (24`)
Таким образом, при каждом всякой непрерывной функции 
на , удовлетворяющей требованию
,
поставлен в соответствие ряд Фурье-Бесселя
, (25)
коэффициенты которого определяются формулами
. (25`)
Можно доказать, что система функций 
на , ортогональная относительно веса , замкнутая. В частности, если ряд Фурье-Бесселя (25) равномерно сходится к порождающей его непрерывной функции .
Можно показать, что если 
и непрерывная на и кусочно-гладкая на функция, то ряд Фурье-Бесселя этой функции сходится к ней при 
.
Похожие работы
... К. Лавриновича «Фридрих Вильгельм Бессель, 1784 – 1846: Астроном, геодезист, математик»,[2] а также справочные издания и энциклопедии, в том числе Брокгауза и Евфрона. §1. Начало научной деятельности Бесселя Немецкий астроном и математик Фридрих Вильгельм Бессель родился в небольшом городе Минден на северо-западе Германии в семье мелкого чиновника в 1784 году. С 15 лет должен был встать на ...
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
... В.В. О построении собственных значений и функций одной газодинамической задачи Франкеля // Математическое моделирование. 1990. Т. 2. № 10. С. 100-109. Моисеев Е.И. о решении вырождающихся уравнений с помощью биортогональных рядов // Дифференц. уравнения. 1991. Т. 27. № 1. С. 94-103. Мамедов Я.Н. О некоторых задачах на собственные значения для уравнения смешанного типа // Дифференц. уравнения
... к задаче [6]: найти регулярное в области решение уравнения (1), непрерывное вместе с производной в замкнутой области и удовлетворяющее граничным условиям (4) и . Решение этой задачи задается формулой : где – функция Грина этой задачи для уравнения . (28) Функция Грина выражается через фундаментальные решения уравнения (28), которые имеют вид: где ; ; – функция Бесселя. Функции , ...
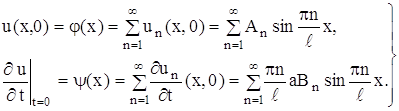
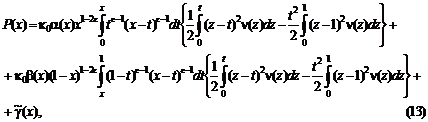
0 комментариев