Навигация
3. Дистрибутивные решётки.
Определение: Решётка ![]() называется дистрибутивной, если для
называется дистрибутивной, если для ![]() выполняется:
выполняется:
1. ![]()
2. ![]()
В любой решётке тождества (1) и (2) равносильны. Доказательство этого факта содержится в книге [1], стр. 24.
Теорема: Решётка ![]() с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида
с 0 и 1 является дистрибутивной тогда и только тогда, когда она не содержит подрешёток вида
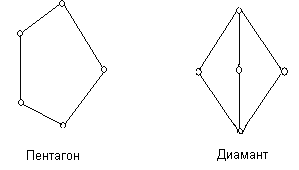
Доказательство этого факта можно найти в книге [2].
Далее под словом “решётка” понимается произвольная дистрибутивная решётка с 0 и 1 (причём ![]() ).
).
Определение: Непустое множество ![]() называется идеалом в решётке
называется идеалом в решётке ![]() , если выполняются условия:
, если выполняются условия:
1. ![]()
2. ![]()
Определение: Идеал ![]() в решётке
в решётке ![]() называется простым, если
называется простым, если
![]() или
или ![]() .
.
Идеал, порождённый множеством Н (т.е. наименьший идеал, содержащий H), будет обозначаться (Н]. Если Н = {a}, то вместо ({a}] будем писать (a] и называть (a] главным идеалом.
Обозначим через I(L) множество всех идеалов решётки L. I(L) будем называть решёткой идеалов.
Определение: Решётки ![]()
![]() и
и ![]()
![]() называются изоморфными (обозначение:
называются изоморфными (обозначение: ![]() ), если существует взаимно однозначное отображение
), если существует взаимно однозначное отображение ![]() , называемое изоморфизмом, множества
, называемое изоморфизмом, множества ![]() на множество
на множество ![]() , такое, что
, такое, что
![]() ,
,
![]() .
.
4. Топологические пространства.
Определение: Топологическое пространство – это непустое множество ![]() с некоторой системой
с некоторой системой ![]() выделенных его подмножеств, которая удовлетворяет аксиомам:
выделенных его подмножеств, которая удовлетворяет аксиомам:
1. Пустое множество и само пространство ![]() принадлежит системе
принадлежит системе ![]() :
: ![]() .
.
2. Пересечение любого конечного числа множеств из ![]() принадлежит
принадлежит ![]() , т.е.
, т.е. ![]() .
.
3. Объединение любого семейства множеств из ![]() принадлежит
принадлежит ![]() , т.е.
, т.е. ![]() .
.
Таким образом, топологическое пространство – это пара <![]() ,
, ![]() >, где
>, где ![]() - такое множество подмножеств в
- такое множество подмножеств в ![]() , что
, что ![]() и
и ![]() замкнуто относительно конечных пересечений и произвольных объединений. Множества из
замкнуто относительно конечных пересечений и произвольных объединений. Множества из ![]() называют открытыми, а их дополнения в
называют открытыми, а их дополнения в ![]() замкнутыми.
замкнутыми.
Определение: Пространство называется компактным, если в любом его открытом покрытии можно выбрать конечное подпокрытие.
Определение: Подмножество пространства называется компактным, если в любом его открытом покрытии можно выбрать конечное подпокрытие.
Определение: Топологическое пространство называется ![]() - пространством, если для любых двух различных его точек существует открытое множество, содержащее ровно одну из этих точек.
- пространством, если для любых двух различных его точек существует открытое множество, содержащее ровно одну из этих точек.
Глава 2.
0 комментариев