Навигация
Доказательство имеет целью установить, что построенная фигура действительно удовлетворяет условию задачи
3. Доказательство имеет целью установить, что построенная фигура действительно удовлетворяет условию задачи.
Доказательство проводится в предположении, что каждый шаг построения может быть выполнен.
4. Исследование. При анализе, построении обычно ограничиваются отысканием одного какого-либо решения, предполагая выполнимость шагов построения. Идя полного решения задачи нужно выяснить:
1) всегда ли (т.е. при любом ли выборе данных) можно выполнить построения избранным способом;
2) можно ли и как построить искомую фигуру, если для какого-нибудь выбора данных указанный способ построения не пригоден;
3) сколько решений имеет задача при каждом возможном выборе данных.
Эти вопросы составляют содержание исследования. Итак, исследование ставит цель - установить условия разрешимости и определить число решений.
Практически исследование проводят по ходу построения, рассматривая каждый шаг построения на возможность и единственность.
Однако такое исследование связано с данным способом построения. В этом случае остается открытым вопрос: нет ли других решений при другом способе решения. На этот вопрос отвечают с помощью указанного выше приема: доказывают, что произвольное решение данной задачи совпадает с одним из уже полученных решений.
Для иллюстрации сказанного рассмотрим следующий пример.
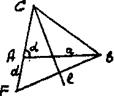
Задача. Построить треугольник, если известны: длина основания а, угол при основании α и разность двух других сторон d.
Решение. Заметим, что в условии задачи не указаны инструменты. B таких случаях будем полагать (как и в школе), что задачу надо решить с помощью линейки и циркуля.

![]()
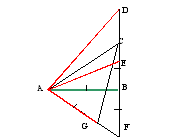
![]() Анализ. Поиск решения задачи проведем, полагая задачу решенной. Пусть ∆ABC - искомый треугольник: AB = a, AC–BC = AD=d,
Анализ. Поиск решения задачи проведем, полагая задачу решенной. Пусть ∆ABC - искомый треугольник: AB = a, AC–BC = AD=d, ![]() = α. Замечаем, что ∆АВD = определен по двум сторонам и углу между ними.
= α. Замечаем, что ∆АВD = определен по двум сторонам и углу между ними.
Третья вершина С искомого треугольника может быть найдена как точка пересечения луча АD и прямой l - серединного перпендикуляра отрезка ВD). Иначе говоря план решения найден, отроим треугольник ∆АВD, а затем и третью вершину С.
Построение. В этом пункте реализуем план решения.
Строим последовательно:
![]()
![]()

1) ![]()
2) l, l – серединный перпендикуляр отрезка BD;
3) C, C = [AD) ∩ l.
Треугольник АВС – искомый.
Доказательство. Действительно, ∆АВС удовлетворяет всем условиям задачи, т.к. по построению
АВ = а, АС – ВС = АD = d, BAD = α.
Исследование. Проверил каждый шаг построения на осуществимость и единственность. Первый шаг возможен и единственен тогда и только тогда, когда 0<α<π. Второй шаг возможен и единственен всегда. Третий шаг возможен и единственен тогда и только тогда, когда α< а cos α. Действительно, если d < a cos α, то прямая l пересекает луч AD. Если же d = a cos α , то l и AD, поэтому треугольника, удовлетворяющего условию задачи, не существует. В том случае, когда d < a cos α, прямая l пересекает луч DА. В этом случае также задача не имеет решения.
Но вернемся к анализу. У нас задача решена, предполагая, что α лежит против меньшей из двух боковых сторон. Если α лежит против большей стороны, то предыдущий метод построения не проходит. Как быть? По теории мы должны и для этого случая дать решение. Нетрудно убедиться, что ΔABF определен (a,d и угол π - α). Построение, доказательство и исследование провoдятcя так же, как и выше.
Необходимо еще выяснить: вcе ли решения найдены. Да, все, так как если бы каким-то способом построить треугольник по a, d и α то этот треугольник был бы равен одному из указанных треугольников (это легко доказать через ).
Основными являются три: метод геометрических мест (ГМТ), метод геометрических преобразований, алгебраический метод.
Метод геометрических мест (пересечения фигур).
Сущность метода: решение задачи сводит к построению некоторой точки (основного элемента построения), подчиненной двум условиям. Отбрасывают одно из этих условий и строят ГМТ Ф1 , удовлетворяющих первому условию, потом Ф2 - ГМТ, удовлетворяющих второму условию. По соответствующей аксиоме конструктивной геометрии можем сказать Ф1∩Ф2 = Ø или нет и если ≠ Ø, то считать построенным пересечение Ф1 ∩ Ф2. Точки Ф1 ∩ Ф2 и только они удовлетворяют обоим условиям одновременно. Точки пересечения и только они дают решение задачи.
Заметим, что успех от применения этого метода полностью зависит от знания конкретных ГМТ. Наиболее часто применяются следующие геометрические места:
ГМТ 1. Множество точек плоскости, каждая из которых равноудалена от двух данных точек А и В, есть серединный перпендикуляр отрезка АВ.
ГMT 2. Множество точек, находящихся на данном расстоянии от данной прямой, есть две прямые, параллельные данной и отстоящие от нее на данном расстоянии.
ГМТ 3. Множество точек, каждая из которых равноудалена от двух данных параллельных прямых, есть прямая, являющаяся их осью симметрии.
ГМТ 4. Множество точек, каждая из которых равноудалена от двух пересекающихся прямых, есть две взаимно перпендикулярные прямые, содержащие биссектрисы углов, образованных данными прямыми,
ГМТ 5. Множества точек плоскости, из которых отрезок АВ виден под прямым углом, есть окружность (без точек А и В ), построенная на отрезке АВ как на диаметре.
ГМТ 6. Множество точек плоскости, из которых отрезок АВ виден под углом α, где α ≠ 90º, α ≠ 180º , есть две дуги с общими концами А и В (без точек А и В), симметричные относительно прямой АВ.
ГМТ 7. Множество точек плоскости, из которых данная окружность видна под углом α, где α ≠ π, есть окружность,- концентрическая с данной, радиус которой больше радиуса данной окружности.
ГМТ 8. Множество точек, делящих всевозможные хорда окружности (O, ОА), проведенные через точку А окружности, в одном и том же отношении λ, где λ > 0, есть окружность (без точки А) с центром на прямой ОА, проходящая через точку А. Если λ = 1, то эта окружность построена на отрезке ОА как на диаметре.
ГМТ 9. Множество точек плоскости, для каждой из которых разность квадратов расстояний от двух данных точек А и В постоянна, есть прямая, перпендикулярная прямой АB.
ГМТ 10. Множество точек плоскости, для каждой из которых сумма квадратов расстояний до двух данных точек А и В равна а2, есть окружность с центром в середине отрезка АВ, если 2а2>AB2; середина отрезка AB, если 2a2 = AB2; и пустое множество, если 2a2<AB2.
ГМТ 11. Множество точек плоскости, для каждой из которых отношение расстояний до двух данных точек А и В постоянно и отлично от единицы, есть окружность с центром на прямой АВ (окружность Аполлония).
Для иллюстрации метода ГМТ решим следующую задачу.
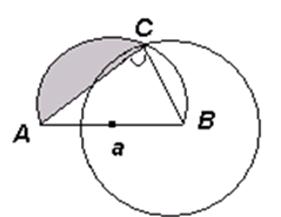
Задача. Построить треугольник, если известны: длина основания а, угол при вершине α и отношение боковых сторон λ, λ ≠ 1.
Решим методом ГМТ.
Анализ. Две вершины А и В искомого треугольника легко построить. Задача сводится к построению точки С. Точка С должна удовлетворять следующим двум условиям: 1) точка С принадлежит сегменту, вмещающему данный угол α; 2) точка С принадлежит окружности Аполлония.
ς α
Построение. Строим последовательно: а) отрезок АВ, АВ = 0; б) сегмент А ς В, вмещающий данный угол α; в) окружность Аполлония на отрезке АВ; г) точку С , принадлежащую пересечению сегмента А ς В и окружности Аполлония.
Треугольник АВС - искомый.
Доказательство и исследование предлагаем читателям провести самостоятельно.
Метод геометрических преобразованийСущность метода: при решении задачи, и прежде всего на первом этапе – анализе, наряду с данными и искомыми фигурами рассматривают другие фигуры, полученные из данных или искомых фигур (или их частей) с помощью некоторого геометрического преобразования (ГП). В зависимости от того, какое (ГП) выбрано, говорят о той или иной разновидности метода ГП (метод параллельного переноса, гомотетии, инверсии и т.д.). Рассмотрим примеры.
1. Параллельный перенос (ПП).Сущность: наряду с данными и искомыми фигурами рассматривают другие фигуры, полученные из указанных фигур (или частей) с помощью ПП.
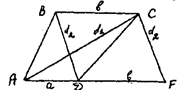
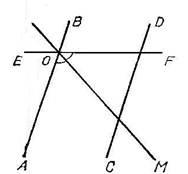
Задача. Достроить трапецию так, чтобы ее основания и диагонали были соответственно равны четырем данным отрезкам.
![]()
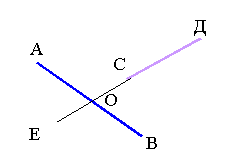
![]() Анализ. Пусть ABCD - искомая трапеция. Сделаем параллельный перенос плоcкости, определяемый вектором ВС: ВС : BD → CF.
Анализ. Пусть ABCD - искомая трапеция. Сделаем параллельный перенос плоcкости, определяемый вектором ВС: ВС : BD → CF.
Треугольник ACF определен по трем сторонам: AF = a + b, AC = d1, CF = d2.
План решения ясен. Предлагаем читателям завершить решение этой задача.
2. Осевая симметрия.Задача. Даны прямая l и две точки А и В, принадлежащие одной плоскости, определяемой прямой l. Найти такую точку Х![]() l, чтобы сумма АХ + ХВ была минимальной.
l, чтобы сумма АХ + ХВ была минимальной.
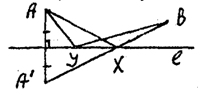
Уклонимся от схемы. Рассмотрим Sе. Пусть A′ = Se (A), X = A′B ∩ l. Покажем, что Х - искомая точка. В самом деле, для любой точки
Y![]() l: AX + XB = A′B < A′Y + YB = AY + YB (Y ≠ X).
l: AX + XB = A′B < A′Y + YB = AY + YB (Y ≠ X).
Исследование. Задача всегда имеет решение, причем единственное.
3. Поворот.Задача. Даны: угол АОВ и точка С внутри него. Построить равносторонний треугольник, одна вершина которого совпадает о точкой С, а две другие лежат на сторонах данного угла.
Анализ. Пусть ∆СDE - искомый. Сделаем поворот плоскости вокруг точки С на угол 60°: R60º (D) = E, R60º (OB) = O′B′, причем E = OB ∩ O′B′. Аналогично находим положение точки D: D = OB ∩ Rc-60º(OA).
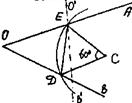
Построение очевидно. Доказательство и исследование предлагаем провести самостоятельно.
Похожие работы
... документации немалая роль отводится чертежнику-конструктору. Он выполняет рабочие чертежи отдельных деталей по чертежу общего вида изделия(при этом используются геометрические построения),разработанного конструктором, предопределяет технологию изготовления отдельных деталей в зависимости от наличия на предприятии технологического оборудования, отрабатывает конструкции деталей на технологичность и ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
... прямых и т.д.; углубить имеющиеся знания по геометрии. Гипотеза: мы предполагаем, что сможем решить некоторые геометрические задачи на построение, используя не классический набор инструментов (циркуль и линейку), а набор из циркуля и короткой градуированной веревки. Задачи о построении на местности Геометрия зародилась в глубокой древности, она изучает форму и взаимное расположение фигур в ...
... расстояния между точками довольно велики и нет таких линеек и циркулей, которые могли бы помочь нам. Да и вообще чертить на земле какие-либо линии затруднительно. Таким образом, построения на местности, основываясь на геометрических законах, имеют свою специфику: Во – первых, все прямые не проводятся на земле, а прокладываются, т. е. отмечается на них, например, колышками, достаточно густая сеть ...


0 комментариев